你是否有想過,學了這麼多年的數學,那些公式、定理是怎麼蹦出來的?
事實上,教科書受限於課程框架的限制,是沒辦法說太多事情。
否則每一本課本都編得跟大一微積分原文書一樣,既不環保,又增加學生攜帶的難度。
這也是我近幾年一直在推廣數位化教學的原因之一,一台ipad放入成千上萬的數位教材,
分門別類,直接在上面做筆記,既輕便又容易保存。
過去曾經有七年級家長跟我反應,說小孩書包好重,本來個子就很小了,
又長時間重壓,真擔心孩子因此長不高。
我們耗費在印刷上的成本太高了,然而用完的書本,學生會怎麼處理呢?
大多數的學生當然直接丟到資源回收箱。前幾天我看到有學生直接將書本一頁頁撕下來,
做成紙盒。雖然我不是這麼鼓勵撕書本,但是比起直接丟回收箱,又可以二次利用,
好像也沒什麼不好。

另外,當你在看這篇文章,應該也不會介意我在這裡閒聊幾句,
在實體教科書上閒聊,可能因此擴增篇幅,增加書本的厚度,造成困擾。
但是我在這裡閒聊,說不定還可以降低你閱讀的門檻。
這也是寫部落格文章的優點:更有彈性,簡潔、易於推廣。
回歸正題,今天我們要來聊聊這個美麗的數學公式:$$e^{i\pi}+1=0$$
這是個非常美妙的公式,因為它串連了「指數」與「三角函數」,僅僅用+、×、指數運算,
就將五個很特別的常數 \(1\)、\(0\)、\(i\)、\(\pi\)、\(e\) 連結在一起。
在影集博士熱愛的算式中,就有提到這一個式子,有興趣的讀者不妨去找來看。
以下是單維彰教授的分享:
說到這些常數所採用的符號,就不得不提一下,
歷史上重量級的數學家 – 歐拉(Leonhard Euler,1707年4月15日—1783年9月18日),
關於歐拉的生平,可以在網路上搜尋到一堆資料,這裡就不再贅述。
我們只要知道幾點:
第一、歐拉是一個非常多產的數學家,記憶力超好,而且有著非凡的數學直覺。
發表超過500篇研究論文,20多本專書。1783年逝世後,還留有超過300份手稿。
第二、歐拉的晚年雙目失明,卻仍然用口述的方式做研究,並在此期間完成生平近一半的著作。
第三、我們很多符號使用的習慣,起源於歐拉。
例如:函數的寫法 \(f(x)\)、虛數的寫法 \(i\)、圓周率符號 \(\pi\)、連加的符號 \(\Sigma\)、自然對數的底數以 \(e\)表示。
總而言之,歐拉是一位數學領域的開創者,在歷史上有著舉足輕重的地位。
接著,我們來聊聊常數 \(e\)。
\(e\) 是什麼?
首先,它與複利計算有著密切的關係,這部份,
我在日前寫的一篇文章「【教學】關於歐拉數的探索之旅 – 高中數學課本沒寫出來的事 – 高中升大學銜接」
有提及,我們很快來複習一下:$$e=\lim_{n\to\infty}(1+\frac{1}{n})^n \tag{1}$$
簡單來說,我們在計算複利的過程中,考慮了一個極端的情況:
本金\(P=1\),利率\(r=1\),經過 \(n\) 期複利後,可得本利和 $$S=(1+\frac{1}{n})^n$$
然後在該篇文章中,我也證明了數列 \(a_n=(1+\frac{1}{n})^n\) 收斂,而那個收斂值,就令為常數 \(e\)。
過程中,我們發現,可將常數 \(e\) 寫成如下形式 $$\sum_{n=0}^{\infty}\frac{1}{n!}$$
另一方面,常數 \(e\) 關乎雙曲線下的面積計算。如下圖所示:
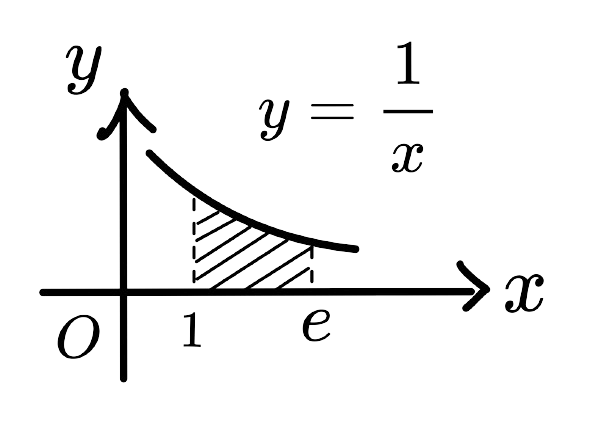
令 $$f(x)=\int_{1}^x\frac{1}{t}dt$$ 函數 \(f(x)\) 表示函數 \(\frac{1}{t}\) 在區間 \([1, x]\) 上與 \(x\) 軸圍出來的區域面積。
而常數 \(e\) 便是使得 \(f(x)=1\) 所在的 \(x\) 值。
我們便將此函數 \(f(x)\) 定義為以 \(e\) 為底數的對數函數 \(log_e x\),符號可簡記為 \(lnx\)。
你是否有發現,\(lnx\)的微分結果不能按照導函數的原始定義直接導出,
而必須使用微積分基本定理:$$\frac{d}{dx}lnx = \frac{d}{dx}\int_1^{x}\frac{1}{t}dt= \frac{1}{x}$$
接著,歐拉在第(1)式中,以\(\frac{x}{n}\) 取代 \(\frac{1}{n}\),定義了函數 $$e^x:=\lim_{n\to\infty}(1+\frac{x}{n})^n$$
使用二項式定理將 \((1+\frac{x}{n})^n\) 展開,可得 $$\lim_{n\to\infty}(1+\frac{x}{n})^n = 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+…$$
有趣的事情來了,歐拉做了一個大膽的動作,就是將指數 \(x\) 以 \(ix\) 取代,此時可得
$$e^{ix}=1+\frac{ix}{1}+\frac{(ix)^2}{2!}+\frac{(ix)^3}{3!}+\frac{(ix)^4}{4!}+…$$
然後繼續冒險,歐拉將此無窮級數重新排序,將實部與虛部分開,改寫如下:
$$(1-\frac{x^2}{2!}+\frac{x^4}{4!}-…)+i(x-\frac{x^3}{3!}+\frac{x^5}{5!}-…)$$
一般來說,無窮級數的排序一旦改變,也許斂散性也會跟著改變;即使此級數依然收斂,
但是收斂值也不一定會相等。然而,這是個很好的函數,這個動作並未影響其正確的結果。
細節的部份,在這裡就先不談了。
最後要說的是,在歐拉的時代,已經知道正餘弦函數的無窮級數表示方式分別如下:
$$cosx=\sum_{n=0}^{\infty}\frac{(-1)^n x^{2n}}{(2n)!}, \ sinx = \sum_{n=0}^{\infty}\frac{(-1)^nx^{2n+1}}{(2n+1)!}$$
因此可得 $$e^{ix}=cosx+isinx$$
此美妙的公式呼之欲出 $$e^{i\pi}=-1$$
這篇文章就先寫到這邊,希望足夠淺顯易懂。
如果你對這樣的內容有興趣,
歡迎訂閱數學數位學習電子報,有新文章發佈會寄e-mail通知囉。





No comments! Be the first commenter?