近幾年我在完全中學任教,教了幾年的國中數學。
除了對於108課綱的內容有了比較全面的了解之外,
最大的收穫,就是能夠體察這個階段學生的想法與思考方式。
很幸運的是,我遇到了很多很優秀,性格很好的學生。
我教他們數學,他們也帶給我很多樂趣及難忘的回憶。
這篇文章,我要重回七年級的課堂,來談談數學的四則運算,
並且從內容去反思,我們的教與學,是如何呈現,
能否貼近數學的本質,是否有改善「教」與「學」的方法?
首先,關於數學教育,我想分享一段話:
數學是理性文明的產物,是一門要講道理的學問。
不論教與學,都應展現提問、思考、說理的過程。
多問幾個為什麼,是學習數學的基本精神與態度。
就我在國中課堂的觀察,不少學生學習數學有以下六個特徵:
1. 記解法:將詳解放旁邊,不會寫的題目,輕易看詳解
2. 盲目刷題:會的題目重複寫,不會的題目沒有整理;結果錯的題目,下次還是錯。
3. 訂正不確實:上進度時比較專心,檢討作業時卻漫不經心
4. 不會寫算式:只會寫選擇題與填充題,不太會寫計算題與證明題
5. 害怕是非題:只想計算,不重視觀念,無法分辨文字敘述中細微的差異。
6. 無法理解題意:題目看懂了就會寫,但就是看不懂題目。
這六個特徵,揭露了學習數學的不良習慣或是沒有培養出好的習慣。
也就是說,如果想要學好數學,就應該避免以上六個情況。
這也就是為什麼有些學生,國小、國中時數學尚可,到了高中後便倍感吃力。
因為很多學生學習數學只想學招式(記解法、作答技巧),
而不知修習內功(建立基礎觀念、說理、提問與論證),
應付小範圍的考試或是某個階段的課業還可以,
長時間下來,除了成績難以突破之外,也可能破壞了學習的興緻。
以上這段話很重要,但很少學生聽得進去。
只要學生願意改變,有意識得進行調整,刻意練習
相信數學能力會隨著時間的累積而逐漸提升。
另一方面,在課堂上,即使老師有心,
但也不一定有時間分享這些觀念。
因此我將其寫成部落格文章,
提供學生以及家長們閱讀參考。
多問幾個為什麼,然後試著說道理
回到七年級的課堂,關於數字的四則運算,相信學生寫過不少,
但是當我們在做這些數字的運算時,是否有想過為什麼?
- \(0\) 為什麼不能當除數?
- 為什麼負負得正?
- 為什麼運算時要先乘除後加減?
網路上經常討論的問題:\(6÷2\times(1+2) = ?\) - 為什麼 $$\frac{b}{a}\times \frac{d}{c} = \frac{bd}{ac}?$$
關於第1個問題,舉個例子來說吧,$$6÷0=?$$
如果我們將其理解為,6個蘋果給0個人分,每個人分多少?
有學生直接回答0個。
不對呀,如果是 \(0÷6\),表示0個蘋果給6個人分,每人分0個,
這沒問題。但是6個蘋果分給0個人,怎麼會是0個呢?
從運算的規則來看,$$6÷3 = 2 \longleftrightarrow 2\times 3 = 6$$ 那麼
$$6÷0=? \longleftrightarrow 0\times ? = 6$$ 沒有任何數乘以0等於6,因此這個數不存在,
也就是說,\(6÷0\) 沒有意義。
按照這個觀點,那麼 \( 0÷0 \) 也沒有意義嗎? $$0÷0=? \longleftrightarrow 0\times ? = 0$$
\(0\) 乘以任何數都等於 \(0\),也就是說 \(0÷0\) 無法確定是多少。
因此,課堂上,我們就直接說,如果除數為 \(0\) 或者一個分數的分母為 \(0\) 沒有意義。
實際上,\(\frac{0}{0}\) 這種情況,還有很多故事可以說。
像是到了大學微積分,有了極限的概念,一個函數取極限後,
如果出現 \(\frac{0}{0}\) 的形式,我們將其稱為不定型。
接著就可以開心得使用羅必達法則,這個之後再談。
總之,我們在寫數字的除法時,記得除數不能為0,
當我們在寫分數時,分母不能為0。
反之,如果寫成分數的形式,那麼就表示分母不會是0,
這在我們使用未知數表示分數時,學生時常會提出的問題。
第2個問題:為什麼「負負得正」?
相信大家學到這一段時,一定背過這個口訣:
正正得正、正負得負、負正得負、負負得正。
那麼那什麼負負會得正呢?
不妨帶個數字來看看吧:\((-2)\times 3 = ?\)
我們可以怎麼理解?
如果你每天向同學借2元,連續借了3天,會欠同學多少錢?
這個比喻大家都可以理解,「負」可以解讀為「負債」,
一天負債2元,將此負債放大為原來的3倍,就是負債6元。
也就是說 $$(-2)\times 3 = -6$$
那麼 \((-2)\times (-3)\) 會是多少呢?
因為多了一個負號,其值與\((-2)\times 3\)是不相同的,
因此 \((-2)\times (-3)=6\) 是合理的。
換個解釋方式,我們知道 \(-(-1)\) 表示 \(-1\) 的相反數,
而 \(-1\) 的相反數就是在原點的另一邊,且與 \(-1\)、\(0\) 兩數的距離相等的數,
此數即為 \(1\),因此負負得正。
或者觀察以下運算規律:
$$\begin{aligned}
(-2)\times 3 &= -6 \\
(-2)\times 2 &= -4 \\
(-2)\times 1 &=-2 \\
(-2)\times 0 &=0 \\
\end{aligned}$$
按照此規律,我們發現以上會形成公差為 \(2\) 的等差數列,因此合理推測
$$\begin{aligned}
(-2)\times (-1) &= 2 \\
(-2)\times (-2) &=4
\end{aligned}$$
因此負負得正!
也可以用更嚴謹的方式來說明:
對於任何(實)數 \(a\),\(-a\) 表示為其相反數。因此 \(a+(-a)=0\)。
那麼 \(-(-a)\) 表示為 \(-a\) 的相反數,即
$$(-a) + [-(-a)] = 0$$
於是 $$(-a)+a=0=(-a)+[-(-a)]$$
因為 \(a\) 與 \(-(-a)\) 都是 \(-a\) 的相反數,而任何數的相反數都是唯一的,因此
$$a=-(-a)$$
接著,將上述例子一般化,說明 $$(-a)\times (-b) = a\times b \tag{1}$$
首先,要先證明 $$a\times (-b) = (-a)\times b = -(a\times b)$$ 這在國中課堂都是輕輕帶過,但卻是可以被嚴格證明的。
由分配律可知 $$a\times b + a\times (-b) = a\times [b+(-b)]=a\times 0 = 0$$ 也就是說 \(a\times (-b)\) 是 \(a\times b\) 的相反數,可以記作 \(a\times(-b) = -(a\times b)\)
另一方面,$$a\times b + (-a)\times b = [a+(-a)]\times b = 0 \times b = 0 $$ 也就是說,\((-a)\times b\) 也是 \(a\times b\) 的相反數,可以記作 \((-a)\times b = -(a\times b)\)
最後,應用以上結果,回來說明第 (1) 式:$$(-a)\times (-b) = -[a\times(-b)]=-[-(a\times b)] = a \times b$$
關於負負得正,你是否還有其他解釋方式呢?
第 \(3\) 個問題,為什麼運算時要先乘除後加減?
來看看前陣子在網路上吵得沸沸揚揚得一道問題:$$6÷2\times (1+2)=?$$有人說答案是 \(1\),有人說答案是 \(9\),吵得不可開交。
按照四則運算的規則,應當先乘除,後加減,有括號的先算。
同位階的運算(例如加與減、乘與除),則依循「由左至右」為原則。
那麼計算結果應該是 $$6÷2\times 3 = 3\times 3 = 9$$
然而,為什麼一定非得要先乘除後加減呢,先加減後乘除行不行?
這個問題就好像,為什麼一定非得紅燈停、綠燈走。
紅燈走,綠燈停行不行?
其實也可以,但是如果不統一規定,交通必定大亂對吧。
同樣地,如果四則運算的規則不統一規定,每個人算出來的答案都不一樣,
那一定會造成極大的困擾。
那麼,我們可以進一步問,這麼規定是不是有什麼好處?
的確,如果每種規定都可以,那麼重點在於統一。
而如果有些規定會帶來比較高的便利性,
那麼我們就採用此規定。
事實上,先算乘除後算加減,這是最方便的最佳選擇!
為什麼呢?
試回想我們在剛學到未知數時,
一個蘋果 \(x\) 元、一顆梨子 \(y\) 元,那麼 5 顆蘋子及 7 顆梨子合計多少元?
我們會寫成 \(5x+7y\) 元。
如果是先加減後乘除,是不是很難表達?
另外,我們在寫多項式時:$$f(x) = x^2 +8x -2$$
以及在以十進位系統表示數字時:$$2024 = 2\times 1000 + 2\times 10+ 4$$
從以上例子可以看出,先乘除後加減的確是比較便利的。
因此,從運算的角度來看,也可以理解為,乘除的位階高過於加減的位階。
所以當遇到乘除與加減混合時,應該先乘除後加減較佳。
你是否還能想到其他先乘除後加減的好處呢?
第 4 個問題,為什麼 $$\frac{b}{a}\times \frac{d}{c} = \frac{bd}{ac}?$$
在課堂上,我從來沒有仔細解釋過這個問題。
不是這個問題不重要,而是課程有進度壓力,學生有考試需求,因此必須做取捨。
所以藉著這篇文章,可以來好好解釋一下:
舉數字來說明:$$\frac{2}{3}\times \frac{6}{4}=?$$
這可以理解為
$$\begin{aligned}
\frac{2}{3}\times \frac{6}{4} &= (\frac{2}{3}\times 6 )÷4 \\
&= \frac{2\times 6}{3} ÷ 4 \\
&= \frac{2\times 6}{3\times 4}
\end{aligned}$$
其中
$$\frac{2}{3}\times 6 = \frac{2}{3} + \frac{2}{3} + \frac{2}{3}+\frac{2}{3}+\frac{2}{3}+\frac{2}{3}$$
因此,由分數的加法規則可知,$$\frac{2}{3}\times 6=\frac{2+2+2+2+2+2}{3}=\frac{2\times 6}{3}$$ 圖示如下:
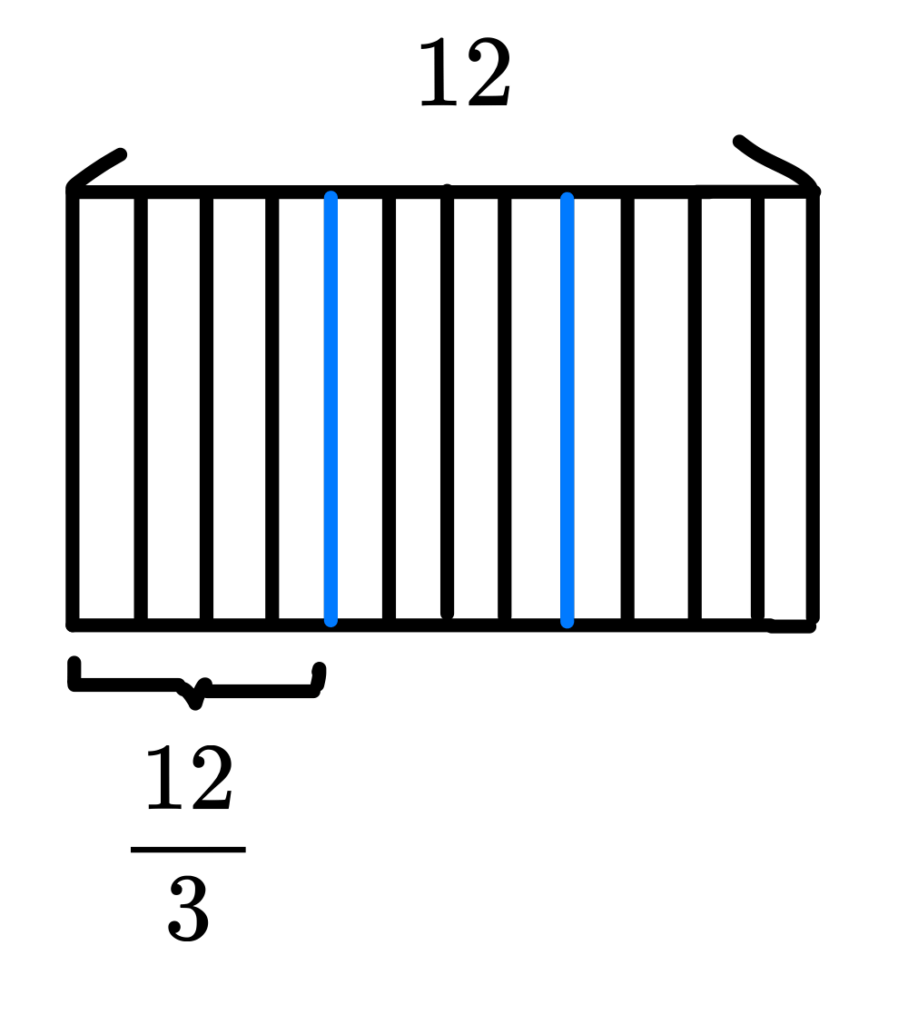
我們將 12 個東西均分為 3 等份,每一等份有 4 個。
另外 \(\frac{2\times 6}{3}÷ 4 \) 可理解為,將以上每一等份再 4 等份,也就是 \(4÷4\),每一等份有 1 個。
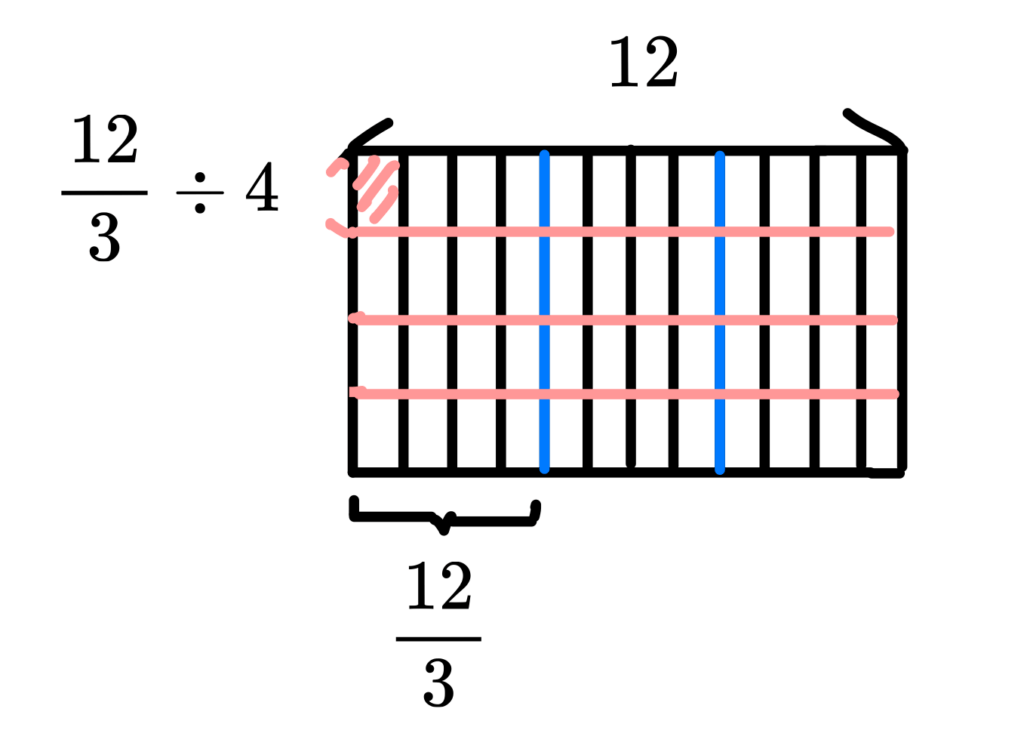
從以上討論與觀察就可以看出其運算規則了。
這篇文章就先寫到這邊,之後會持續分享數學相關科普文章,
歡迎訂閱國中數學數位學習電子報,取得文章發佈通知。







No comments! Be the first commenter?