高中數學第二冊數位教材
hi,歡迎你來到這裡。在這個頁面,我將根據108課綱編寫一套以觀念為主的數位教材,除了有文字的解說,同時搭配網路現有教學資源。讓學生可以自學,觀看影片學習。
整個編寫方式是以部落格的形式呈現,所以盡可能少用符號,多講述觀念。同時還有製作目錄,讀者可以自行點選目錄看你想看的主題。看完後,再按「返回目錄」重新選主題。
另外,這不是單純的高中數學內容,還會加入數學史以及一些延伸題材,目的是不要完全受到課綱的限制,讓有興趣的學生學到該學的內容。
要特別注意的是,這些影片是以108課綱章節的順序選取,但錄製的內容不一定完全符合108課綱的要求,請務必對照課本使用,這只是一個輔助的學習方式,在學校還是要用心聽講,才能學到較完整的知識。
關於108課綱,可參考以下文章:
高中數學108課綱「課程」與「考試」分析、各版本整理及考生的因應方式
歡迎訂閱高中數學數位學習電子報
這個網站專注於製作與研發數位教材,目前已編寫 高一數學第1冊;高一數學第2冊 免費提供給有需要的人使用。
第一章 數列與級數
1-1 數列與遞迴關係
何謂數列?
一堆數「依序」排成一列稱為數列,這裡指的「序」就是指這些數排列的規則。觀察數列規則並推理出某一項的值,是這個單元的學習重點。
等差數列

- 等差數列的一般項 – 均一教育平台
- 判斷一個數列是否為等差數列 – 均一教育平台
- 【例題】等差數列:求第n項 – 均一教育平台
- 【例題】等差數列:兩個數之間共有幾個m的倍數 – 均一教育平台
- 【例題】由等差數列一般項公式判斷公差 – 均一教育平台
- 【例題】等差數列:省錢問題 – 均一教育平台
- 【例題】等差數列:三角形的三內角 – 均一教育平台
- 【例題】等差數列:第幾項之後開始為負數 – 均一教育平台
- 等差中項 – 均一教育平台
- 【例題】等差數列:三項成等差,已知兩項和 – 均一教育平台
- 【例題】等差數列:已知五項成等差,求前兩項、後兩項和 – 均一教育平台
- 【例題】等差數列:兩組三個代數式成等差 – 均一教育平台
- 遞迴關係式:Shgsh Math 提供
等比數列
等比數列又名幾何數列,即一個數列滿足「後項除以前項為一非零定值」稱之。

如果a、b、c三項成等比數列,則b稱為a、c的等比中項,滿足b平方等於a乘以c。因此,這三個數的等差中項即為ac的平方根。
以下影片說明皆由均一教育平台錄製開放使用。
- 【觀念】等比數列
- 【觀念釐清】貌似等比數列的數列
- 【觀念釐清】等比數列與等比中項
- 【觀念釐清】等比數列的公比
- 【觀念釐清】檢查各項變化後的等比數列
- 【例題】求等比數列的公比與特定項
- 【例題】插入一些數使數列成為等比數列
- 【例題】等差與等比的混合
遞迴關係式
遞迴關係式,簡單來說,就是指一種用「遞推」的方式來定義數列的方程式。因此我們可以由遞迴關係式看到第n項與第n項之前的關係。
我們舉熟悉的例子來說,例如,等差數列的「後項」為「前項」加上公差,我們可以寫成以下形式

其中要注意的是,我們的第1項的足標為1,因此遞迴關係式中的足標n必須從2開始。
當然,由遞迴關係式,我們可以逐步寫出每一項,然而,與一般項的差別在於,遞迴關係式無法立即寫下其中一項(除非這一項很前面可一眼看出)。因此,遞迴關係式適合藉由電腦輔助重覆進行快速運算。
此時,我們很自然地問了個問題:要如何由遞迴關係式寫出數列的一般項?反過來問,如何由數列的一般項寫出此數列的遞迴關係式?當然第一個問題比第二個問題困難許多。我們可以由斐波那契數列當例子說明:
數學歸納法
當我們看到一個數列時,第一件事會做什麼呢?答案是,觀察其「規律」。看出規律後,再試著寫出其「遞迴關係式」或「一般項」。
然而,在我們還未寫下一般項之前,通常會先觀察前面幾項,然後再由前面幾項「猜測」可能的一般項。但是我們要如何確保我們的猜測是對的呢?
我們採用的策略是:數學歸納法,其實就是「骨牌效應」的概念。
想像一下,你要如何確保每個骨牌最終全部倒下?首先,第一個要先倒下,接著假設某一個倒下,我們要驗證它的下一個也會倒下。這就是數學歸納法的精神。
但是,數學歸納法扮演的角色只是「驗證」,而不是「推導」。如果要看清楚問題的本質,不能只滿足於驗證其正確性,還要設法了解為什麼會如此?
1-2 級數求和
我們將數列的每一項相加,就形成一個級數(series)。對於有限級數,要如何求出級數和,通常不是件容易的事。我們高中階段,只會處理一些簡單的級數,例如:等差級數、等比級數、平方和級數、立方和級數、等差等比混合型級數、分項對拆型級數。
當然,如果隨便寫一個數列,不一定總有方法寫出其級數和。因此,除非有必要,否則我們不會沒事隨便寫個數列去算級數和。以下是關於求級數和相關的教學影片,我是按照課本學習順序放上連結,歡迎多加利用。
- 級數基本概念及等差級數公式
- 等比級數及其例題
- 等差等比混合型級數的計算:PengTitus老師講解
- 求平方和的證法1:PengTitus老師講解
- 求平方和的證法2:PengTitus老師講解
- 求平方和的證法3:PengTitus老師講解
- PengTitus老師講解
- 求平方和的證法5:PengTitus老師講解
- 求平方和的證法6:Gim老師講解
- 級數立方和

補充說明,對於無窮級數,我們要先判斷這個級數是收斂或發散?對於級數的收斂或發散的判斷有很多方法,這部份在大學微積分有詳盡的說明。
第二章 排列組合與古典機率
排列組合與古典機率是高中數學的重頭戲,然而108課綱已將排列組合弱化至以古典機率所需的內容為主,並且刪除了重複組合,有興趣的讀者可點選連結學習。
2-1 邏輯、集合與計數原理
主題一 邏輯
這一節是為了排列組合做準備。首先介紹一些基本的邏輯概念:何謂命題(或敘述)?連接詞「且」、「或」的介紹、什麼是邏輯的狄摩根定律?「若p則q」命題,充份與必要條件。
邏輯是重要的,但在高中數學課程中並不怎麼受到重視,考題也較少。每次教到這個部份,通常不會有太多時間,簡單帶過之後就要進到集合與計數原理。因此,在這個頁面我希望能稍微講仔細一點,讓學生有比較清晰的認識。如果,想要更全面與進階的課程,可參考:臺大開放式課程:邏輯/共同教育中心 傅皓政
何謂命題(或敘述)?
凡是能判斷「對」或「錯」的語句,就稱為「命題」或是「敘述」。例如:
- 「在平面上的三角形內角和為180度」是正確的敘述。
- 「91是質數」是錯誤的敘述。
- 「太陽從西邊升起」是錯誤的敘述。
命題P的反面就稱為P的「否定敘述」,記作~P。
如果命題P為「真」,則命題~P則為「偽」;反之,命題P為「偽」,則命題~P則為「真」。
舉個例子來看看吧:
命題P:「在平面上的三角形內角和為180度」是正確的敘述。
命題~P:「在平面上的三角形內角和不為180度」是錯誤的敘述。
命題Q:「91是質數」是錯誤的敘述。
命題~Q:「91不是質數」是正確的敘述。
連接詞「且」與「或」
當我們在講述一件事時,很多時候一個敘述是不夠的,須要用到兩個敘述,此時就必須用連接詞連接。
首先,我們要能夠區分「且」與「或」的差別:
簡單來說,P且Q表示P與Q皆成立;P或Q表示P或Q成立即可。
我們用真假值表就一目瞭然了。
若P、Q皆為真,才能保證「P且Q」為真,否則為假。
若P真或Q真,即可保證「P或Q」為真;若P與Q皆為假,則「P或Q」為假。

補充說明:符號∧表示「且」;符號∨表示「或」
舉個例子來看看吧,以下這題是102年學測單選第1題

因為小文的成績不符合參選模範生的資格,所以他沒有滿足一或二這兩個條件。
另外,他的國文考了65分。
這一題學生容易犯的錯誤是,從選項往回推,但這樣做的方向是不對的。我們是希望由題目的條件推論到選項,而不是從選項推論到題目的條件,要小心。
如果小文沒有滿足條件一,那麼表示他的英文成績必定未達70分,數學成績隨意。因此選項(2)不對。
或者,
如果小文沒有滿足條件二,那麼表示他的數學成績不及格,英文成績隨意。因此選項(1)不對。
關於選項(3),那個「但」其實就是「且」的意思,當然不對。
因為小文是沒有滿足條件一或條件二,因此應該選(5)。
邏輯的笛摩根定律
奧古斯塔斯·德摩根是19世紀英國數學家,他首先發現了在命題邏輯中存在著下面兩個關係:
~(P∧Q) ≡~P∨~Q;~(P∨Q)≡~P∧~Q
即
非(P且Q)等價於(非P)或(非Q);非(P或Q)等價於(非P)且(非Q)
凡是被冠上名字的定理、定律,在該領域必定起了重大的作用。這個發現影響了喬治·布爾從事的邏輯問題代數解法的研究。其實我們上面舉的那一題102年學測試題單選題第1題就有用到迪摩根定律了,你發現了嗎?
因為小文不符合參選模範生的資格,意思就是否定(條件一且條件二),也就是不符合條件一或不符合條件二。這就是迪摩根定律。
還有一個驗證迪摩根定律的方式,那就是真假值表。

我們可以很清楚地看到其等價關係。
【教學影片】什麼是邏輯?
「若P,則Q」命題
這是一個很常見的命題,其中P是命題的前提(或假設),Q是命題的結論。
還記不記得國中的幾何證明題,是否都是以這種方式呈現呢?我們簡單列出幾個例子:
- 「若P點與A、B兩點等距,則P點必落在線段AB的中垂線上。」是正確的敘述
- 「若四邊形的對角線等長,則此四邊形為矩形。」是錯誤的敘述
- 「若三角形ABC為正三角形,則角A=60度。」是正確的敘述
再來舉幾個同學剛學到的例子:
- 「若a、b為兩個非負實數,則兩數相加除以2(算術平均數)大於等於兩數相乘開根號(幾何平均數)」
- 「若a是有理數,b是無理數,則a+b是無理數」
關於這個部份,可看看以下影片。
充份條件與必要條件
當命題「若P,則Q」是正確的,則稱P是Q的「充份條件」,記作「Q => P」,且稱Q是P的必要條件。
例如:
- 「若下雨,則地溼」。其中「下雨」是「地溼」的充份條件;「地溼」是「下雨」的必要條件。
- 「若A是菱形,則A是平行四邊形」,其中「A是菱形」是「A是平行四邊形」的充份條件;「A是平行四邊形」是「A是菱形」的必要條件。
另外,當命題「若P,則Q」與「若Q,則P」皆正確時,則稱P是Q的充要條件,或Q是P的充要條件,可記作
「P <=> Q」。在原文是這樣描述的,P if and only if Q,簡記為 P iff Q。
我們來舉幾個例子看看:
- P:A是正三形;Q:A是等腰三角形。其中P是Q的充份非必要條件。
- P:x是質數;Q:x是奇數。其中P是Q的非充份且非必要條件。
- P:x是實數;Q:x是有理數。其中P是Q的必要非充份條件。
- P:x平方等於1;Q:x等於正負1。其中P是Q的充份且必要條件(簡稱充要條件)。
邏輯的介紹就到這邊,讓我們來看看教學影片吧:
最後,有一道有趣的邏輯問題,供讀者想想:
A、B兩男士好奇地詢問C女士的年齡,C女士列出11個可能的答案:
35、36、38、42、45、46、51、55、57、61、62
接著C女士將她年齡的十位數告訴A男士,將她年齡的個位數告知B男士。
A男士說:「我不知道C的年齡,但我想B也不知道。」
B男士說:「我原本也不知道C的年齡,但現在也知道了。」
A男士說:「哦,那現在我也知道了。」
請問C女士的年齡是幾歲?
主題二 集合
什麼是集合?
這可不是一個好回答的問題,因為集合是很抽象的概念。我們在高中階段,盡可能舉具體的例子讓同學容易理解。
簡單來說,集合是具有某種特性的事物的整體,或是一些確認物件的匯集。構成集合的事物或物件稱作元素或是成員。集合的元素可以是任何事物,可以是人,可以是物,也可以是字母或數字等。
看到以上的定義,估計很少人可以馬上領會到什麼是集合。
我們可以舉一個簡單且生活化的例子來解釋,例如,某個班上有40位同學,每位同學有一個座號,不妨假設為1~40號。那麼1~40這40個數字,就構成了一個集合,每一位同學稱為此集合的一個元素。再者,在課堂中,有時候老師會讓同學分組討論,那麼每一組就形成一個比較小的集合,稱為子集合。
另外,在集合的性質方面,我們可以想像以下的情況:
- 在班上,通常每隔一段時間(通常是段考後)會換座位,順序變了,班上成員會改變嗎?
- 老師在點名時,喊了一位學生的名字,學生沒聽清楚,老師又喊了一次。那麼班上成員會改變嗎?
- 有時候老師叫同學的名字,有時候叫座號,那麼班上成員會改變嗎?由此可知,可以辨別即可,名稱不重要。如果恰巧班上有兩位同學姓名一樣,當然叫座號會比較適合。
- 一個學生,他有可能是班上的成員,否則便不是班上的成員,不會存在模稜兩可的情況。
由以上可知,集合中的元素,不計順序、不計重複、具有確定性。
雖然這不是個嚴謹的例子,但對於現階段的中學生入門,相信還是會有些幫助的。
說到集合,當然就是要提一下這位19世紀末20世紀初的德國數學家,康托(G.Cantor,德國,1845~1918)。
年輕的康托爾在27歲的時候,就在數學上表現出優秀的數學天賦,他用有理數列構造實數R,在數學發展歷史上,這是「前無古人」的創意。
我永遠也忘不了,以康托爾名字命名的集合:Cantor Set
這個要到大學的高等微積分課程才會介紹,有趣趣的資優生可點選Cantor Set連結參考。
關於集合比較細節的基本介紹,就請同學觀看以下影片學習囉,重點摘錄如下:
- 集合的表示法:列舉法、描述法
- 子集合、冪集合的介紹
- 集合的運算:何謂交集、聯集、差集
- 名詞解釋:什麼是宇集、補集?
集合的迪摩根定律
對比於邏輯的迪摩根定律,集合的版本如下:

這是兩個集合的迪摩根定律,但既然冠上名字,事情當然沒有這麼單純。事實上,對於n個集合,甚至是無窮多個集合,這個定律依然成立。
可以畫出文氏圖觀察,兩個集合的版本顯然成立。如果要較為嚴謹的論證,可以證明等號兩邊的集合互為對方的子集即可。
例如:如果x是「A交集B的補集」裡的一個元素,那麼x不在「A交集B」裡。換句話說,x不在A裡或不在B裡,因此得出x落在A的補集或B的補集裡。另一方面,如果x不在集合A裡面,或不在集合B裡面,那麼x必定不在集合A與B的交集裡。
主題三 計數原理
若將邏輯與集合比喻為排列組合的內功,那麼計數原理則像是排列組合的基本招式。大家都會數數,但怎麼數才會有效率,則是我們學習的重點。這裡介紹幾種計數方式:窮舉法、樹形圖、加法原理、乘法原理、一一對應原理、取捨原理。
窮舉法
顧名思義,所謂的窮舉法,就是將所有符合條件的方法或情形一一列舉出來的計數方法。這個方法看似麻煩、複雜、又相當費時。然而,在解決很多問題時,窮舉法卻又顯得特別簡單。當然,我們日常使用的窮舉法,都只能解決一些規模較小的問題,對於一些規模較大的問題,我們則要使用電腦輔助計算。
我們舉個簡單的例子來看看吧:
設A-BCD為一個四面體,有一隻螞蟻從A點出發,沿著稜邊走到B點,在每個頂點至多經過一次的條件下,共有幾種走法?
走法會有以下幾種:
- A -> B
- A -> C -> B
- A -> D -> B
- A -> D -> C -> B
- A -> C -> D -> B
提醒同學,我們在列舉時,要有系統且有次序地列舉,才可以避免少列或多列。
樹形(狀)圖
由以上的例子,我們亦可以將所有情形用樹形圖表呈現。關於窮舉法與樹形圖的基礎教學,可參考以下影片:
有興趣的同學可以試試以下例子:
將六個字母 a、a、b、b、c、c 排成一列。若規定第1位必須排a,且相同的字母不能相鄰,問共有多少種不同排法?
加法原理
若完成某件事的方法,依其性質可以分成k類,且第1類有m1種方法、第2類有m2種方法、…、第k類有mk種方法。則完成這件事的方法共有m1+m2+…+mk種。
看完以上的敘述,你覺得關鍵字是什麼呢?有學生認為是「加法」;但是如果是加法,那與我們小學學的加法有什麼區別呢?因此,我認為加法並不是此原理的核心精神,而是「分類」!
為什麼很多人會認為加法原理很簡單,我們來看看課本一開始舉的例子:
若從甲地至乙地只有「公路」與「鐵路」兩種捷徑,其中公路3條,鐵路2條,則從甲地到乙地的路徑選擇共有多少種方法?
你發現了嗎?題目已經分類好了:公路與鐵路。我們只要將兩類的所有可能相加即可得出共有5種方法。因為這個問題已經將最關鍵的分類告訴我們了,當然很容易。
以下是關於加法原理基本觀念說明例:
讀者不妨試試以下這一題:
將21個相同的球全部放入3個不同的袋子,若每袋至少一球,且任兩袋球數和大於第三袋球數,則球數的安排方案共有幾種?
這一題在考什麼?沒錯,它其實是在考加法原理,我們在數數時,發現不容易,因為還沒有分類,我們不知怎麼加才不會亂掉。
答案為55種,你做對了嗎?
以下是加法原理常見例題:
乘法原理
什麼是乘法原理?
若完成某件事要經過k個步驟,且第1個步驟有m1種方法、第2個步驟有m2種方法,…,第k個步驟有mk種方法,則完成這件事的 方法共有m1×m2×…×mk種。
你認為以上文字的關鍵字是什麼?
沒錯,就是分「步驟」。
初學者容易混淆「加法原理」與「乘法原理」的使用時機。分辨方式簡單來說就是,分「情況」則用「加法原理」;分「步驟」則用「乘法原理」。
以下是我認為不錯的教學影片:
下面是加法與乘法原理混合題,試試看吧!

歡迎訂閱高中數學數位學習電子報
2-2 排列
排列的問題大致可分為以下幾類:1. 全取排列 2. 不全取排列 3. 不盡相異物的排列 4. 重複排列
全取排列
在日常生活中,相信大家都有排隊的經驗吧,想像一下有五個人正在排隊上公車,那麼這五個人所有可能的排序會有多少種?這就是全取排列的概念。同樣地,我們將人換成任何相異物,然後去計算會有多少種排法,也是如此。
當然不可能慢慢排,因此須要用到我們上一節學到的計數原理。如果有n件相異物排列,那麼我們可以想成有n個不同的箱子要放進這n件相異物,並且問放法有幾種?
第1個位子有n個選擇,第2個位子剩n-1個選擇,第3個位子剩n-2個選擇,依此類推…,我們可以想成要完成將物品放進這n個箱子,須要經過n個步驟,因此所有可能的放法有n×(n-1)×(n-2)×…×2×1=n!種。
此時同學要去熟悉階層(!)符號並練習其運算操作。
不全取排列
顧名思義,就是我們只取部份的相異物(或人)進行排列。例如:有n個人要坐m個座位,人數不少於座位的情況下,則排列方式有幾種?如果人數與座位一致,那麼這就是全取排列。如果人數多於座位,則我們要先選出m個人,然後再排列,其排列方式有n×(n-1)×(n-2)×…×(n-m+1)種。
常見題型如下:
- 某歌手想從7首歌當中,選出3首歌在演唱會中依序表演,則安排的方案會有幾種?
- 從0、1、2、3、4、5這五個數字中,任取3個數字排列,則可以排成多少個三位數?
- 甲 、乙、丙、丁、戊五人排成一列依序上公車,若甲不排首位、乙不末位,則共有幾種排法?
不盡相異物的排列
前面討論的事物都是不相同的,現在我們來探討含有相同事物的排列。
我們舉個簡單的例子來看看:字母AAABB的排列方式有幾種?
首先我們知道,必定比五個完全相異的字母排列方式少,我們不妨將排列五個相異字母A1A2A3B1B2拆成兩個步驟進行:
步驟1:先排列AAABB,假設其排列數為X
步驟2:將A1、A2、A3與B1、B2各別排列
根據乘法原理,5! = X × 3!×2!,因此可得 X=5!/3!×2!
一般的敘述如下:

不盡相異物排列常見題型如下:分球問題、有順序關係的排列、樓梯問題、信號問題、走捷徑問題。
以下影片有助於同學建立觀念:
有了基本觀念之後,可以試試以下幾道問題:
- 例題01有相同物的排列問題
- 例題02分球問題
- 例題03字母排列問題
- 例題04走捷徑問題
- 例題05有順序關係的直線排列
- 例題06走樓梯問題
- 例題07排數字問題(數字不全取):只要注意0不能排首位即可。這類問題在數字不全取的情況下較常被命題。
- 例題08排數字問題(數字不全取)
重複排列
什麼是重複排列問題?我們舉個例子來看看吧。
一個密碼鎖,有四排數字,每1排數字有0~9這十個數字可供選擇,我們必須這四個數字正確且順序無誤才能打開這個鎖。
每一排有10個選擇,因此所有可能性有10×10×10×10=10000種。
重複排列的問題可以想成「每一個位置可放一個以上的相異物」或「每一個位置可站一個以上的人」。
其他例子像是,坐船問題、倒酒問題、信投入郵筒問題等…皆是此類問題。
我們將以上例子的觀察寫成定義如下:

觀念解說可參考以下影片:
初學者在處理重複排列的問題時,容易混淆「底數」與「指數」應該放入什麼數字。有一個判斷方式提供參考:
我們將可以重複容納的稱為大,不能重複放置的稱為小。「大」放在底數,「小」放在指數。
舉幾個簡單的例子:
- 5封信件放入3個不同郵筒的放法有幾種?郵筒大,信件小,全部放法有3的5次方種。
- 6個人坐3艘船的坐法有幾種?船大,人小,全部坐法有3的6次方種。
- 4種不同酒倒入3個不同的酒杯,不能調酒倒法有幾種?酒大,酒杯小,全部倒法有4的3次方種。
常見例題如下:
2-3 組合與二項式定理
組合的基本概念
初學排列組合的同學,首先要能分辨「排列」與「組合」的差異是什麼?
用一句話概括就是,「差一個步驟」!也就是說,「排列」實際上是經過兩個步驟:1. 先選取 2. 再排列
而組合就是其中的第1個步驟。
因此,如果「從n件不同物中選取k件」排成一列,其排列數為P(n,k);我們將「從n件不同物中選取k件」記作C(n,k)。因此由乘法原理可知 P(n,k)=C(n,k)×k!
從這個定義,我們可以很輕易看出以下幾個性質:
- C(n,0)=C(n,n)=1:n個不同的物品,「完全不選」或是「全部都選」,其方法顯然各只有1種。
- C(n,k)=C(n,n-k):n個不同的物品,從中選取k個的意思就是有(n-k)個沒有被選到;換句話說,選取(n-k)個的意思就是有k個沒有被選到。因此選取k個的方法數與選取(n-k)個的方法數是一樣的。
- C(n,k)=C(n-1, k-1)+C(n-1, k):這個等式稱為巴斯卡定理。這個定理有「代數」與「組合」證法。
代數證法沒什麼學問,就是依照組合符號的定義直接計算即可。組合證法也不難,想像一下,從n個人選出k個人,可以分成兩個情況,假設當中有一個人「甲」,我們在選的時候,甲可能被選中也可能不被選中。
如果甲被選中,則只剩下(n-1)個人再選出(k-1)個人。如果甲未被選中,則從剩下的(n-1)個人選k個人。將這兩種情況相加就是C(n,k),因此證明出巴斯卡定理。
相關閱讀:
關於組合的基本觀念,可觀看以下影片學習:
關於二項式定理
二項式定理簡言之,就是描述了二項式的冪的代數展開:

為什麼要介紹二項式定理呢?比較粗淺的解釋是,組合符號可以用來表示展開後的各項係數。但是站在歷史的觀點,我們可以進一步問,這個定理是誰發現的?動機為何?這個定理有何用途?
一般認為是牛頓於西元1664年~1665年提出,因此又稱為「牛頓二項式定理」。上面提到二項式定理的係數可用來表示「巴斯卡三角形」。牛頓考慮的是廣義的二項式定理,即指數n是「分數」或「負數」的情形,但他並沒有給出證明。一直到1811年才由德國數學家高斯證明。
因此,我們學習的內容是原始問題的特例。
有興趣的讀者,可以參考另一篇文章,標題為「輕鬆談如何教學二項式定理?」。
2-4 古典機率
我們高中學習的機率為古典機率,是由法國數學家拉普拉斯(Pierre Simon, Marquis de Laplace,1749-1827)所定義。拉普拉斯不僅是數學家,同時也是一位天文學家,有法國牛頓之稱。
在日常生活中,隨機現象處處可見。所謂隨機現象是指,我們預期可能會發生,但無法確定是否發生的現象。
例如將一個銅板往上丟,我們可以預期正面或反面會朝上,但卻無法百分之百確定哪一面會朝上。我們買樂透,期待有可能會中獎,但卻無法確定是否會中獎。
我們可以感覺一下,一個銅板往上丟,其「正面朝上」的機會與「買樂透中頭獎」的機會何者較高?直觀來看,當然是前者。可是如果我們要比較,擲兩個公正骰子,「其點數和為4」的機會比較大還是「點數和為8」的機會比較大呢?
換句話說,能否將發生機會的高低,明確地量化,使我們清礎地知道某個「事件」發生的機會有多高(低)?
機率就是將隨機現象量化的工具
以下列出學習機率的順序,可依序點連結觀看影片學習:
何謂樣本空間與事件?
一項試驗中所有可能發生的結果所成的「集合」,稱為這個試驗的樣本空間。樣本空間中的每一個元素,稱為「樣本點」或簡稱為「樣本」。此集合內的「子集合」就稱為一個「事件」。僅含有一個樣本的事件稱為「基本事件」,樣本空間本身稱為「全事件」。

這個定義應該不難理解,舉個簡單的例子來說,投擲一顆骰子,觀察朝上的數字,那麼它的樣本空間就是{1,2,3,4,5,6}。每一個數字都是此樣本空間中的一個「樣本」。擲到偶數點的情況為2、4、6,此集合{2,4,6}就稱為一個事件。
這邊牽涉到不少名詞,你覺得名詞重不重要?
我有遇過一些學生時常說,我只要會算就好了,名詞不重要。但試想想,如果名詞沒有記的話,那麼聽課或討論時,要如何知道對方描述的是哪一件事?或是要如何很快讓對方了解你在說什麼?也許有人會說,我只要看到就知道了。沒錯,但如果每一件事情都是要寫出來才知道在講什麼,是不是比較沒有效率呢?
數學本身是一種語言,因此一定要將每個名詞的意思記清楚,這樣你在使用這個語言才會又快又精確。
古典機率的定義
設一試驗的樣本空間 S 之樣本點有有限多個。當 S 中每個樣本點出現的機會均等時,定義事件A發生的機率為[A的樣本點個數]及[S的樣本點個數]的比值。
這個定義最早是由法國數學家皮耶—西蒙·拉普拉斯(P.S.Laplace, 1749~1827)所提出,因此又稱為「拉普拉斯機率」
教科書對於這位數學家介紹不多,但他有另一個稱號,相信會讓大家印象較為深刻。
因為拉普拉斯於1799年出版了巨著《天體力學》,主要論述行星運動、行星形狀和潮汐,書中第一次提出了「天體力學」的學科名稱。該書是經典天體力學的代表著作,由於這部巨著的出版,拉普拉斯被譽為法國的牛頓。
法國18世紀後期到19世紀初數學界著名的三個人物:拉格朗日(Lagrange)、拉普拉斯(Laplace)和勒讓德(Legendre)。因為他們三位的姓氏的第一個字母為「L」,又生活在同一時代,所以人們稱他們為「三L」。
關於拉普拉斯給出的定義,你認為關鍵字是什麼?
答案是:「S 中每個樣本點出現的機會均等」,我們稱其為「機會均等法則」。用白話一點來說,所謂的機會均等法則就是要將相同的物件視為不同。這也是機率與排列組合不太一樣的地方。
排列組合重視結果呈現出來的「狀態」,而機率重視結果呈現的「方法數」。
例如:袋中有2顆相同白球、3顆相同黑球,則從中取出兩球皆為黑球的情況有幾種?若按照組合的觀點,應該就是1種,但若按照機率的觀點,會有3種。因為即使黑球一樣,但每一顆黑球皆占了一個被取到的機會。因此我們要將3顆黑球皆視為不同。
在這裡要注意的是,我們在計算機率時,才會將每個物件皆視為不同。如果只是要寫出樣本空間,那麼便沒有這樣的限制。以上述例子來說,其樣本空間應該是:{白白、黑白、黑黑},但是如果要計算機率的話,其樣本空間就要寫成:{白1白2、白1黑1、白1黑2、白1黑3、白2黑1、白2黑2、白2黑3、黑1黑2、黑2黑3、黑1黑3}
機率的性質
由機率的定義,可得出以下性質:
- 任何「空事件」的機率為0,任何「全事件」的機率為1
- 任何事件的機率,其數值介於0、1之間(含0、1)
- 某事件的餘事件的機率=1-此事件的機率:反面做法
- 取捨原理
我們將以上敘述用數學符號表示如下:

附帶一提,如果兩事件A、B為互斥事件(即A與B的積事件為空事件),則其和事件的機率為其個別機率相加。

關於機率的問題很多,我們來看看以下幾題,建議先想過後再點入連結看解說喔!
機率相關題型


2-5 數學期望值

期望值是「平均」的概念。舉個例來說,我們通常是如何計算學期成績呢?
假設某校規定:平時成績佔了20%,第一次期中考佔了25%、第二次期中考佔了25%,期末考佔了30%,如果有一位同學平時成績得80分,第一次期中考得70分、第二次期中考得75分,期末考得85分,那麼他的學期成績應該是幾分呢?
學期成績=80×20%+70×25%+75×25%+85×30%:=m1×p1+m2×p2+m3×p3+m4×p4=77.75
換句話說,按照這個比重計算,我們可以期望該生的學期成績為77.75分。
我們再來看看另一個例子:
擲一顆公正骰子,已知擲出1、2、3點可得10元;擲出4、5點可得20元;擲出6點可得50元,求擲骰子一次所得金額的期望值為何?
按照定義,期望值=10×1/2+20×1/3+50×1/6=20(元)
如何解讀?
我們擲這一顆公正骰子,獲得的平均金額為20元,因此期望值也可以解讀為「長期期待值」。這部份留待我們學到了「隨機變數」描述起來會更為清楚。
第三章 數據分析
數據是統計學家的原料,是我們用來解釋事實的數字。所有統計問題所牽涉到的,不外乎蒐集、描述及分析數據,或者思考要如何蒐集、描述及分析數據。
一維數據分析
眾數、中位數、算術平均數、加權平均數、幾何平均數
透過統計,可以從眾多數據中取得關鍵指標,來代表整體數據的特性。一種指標是呈現出資料集中的程度,稱為「均量」,例如:眾數、中位數、算術平均數、加權平均數、幾何平均數、百分位數、四分位數,前三項在國中已學過,我們會略為複習並且做更精確的計算
另一種指標,則是呈現出資料分散的程度,稱為「差量」,例如:全距、四分位距、變異數、標準差,前兩項國中為國中課程內容。
這類以單一的數值來代表整體數據特性的分析,稱為一維數據分析。
接下來,同學可以先看以下影片複習「眾數」、「中位數」、「算術平均數」的基礎內容。
- 什麼是一群數據的「眾數」、「中位數」、「算術平均數」?如何計算?
- 使用「眾數」、「中位數」、「算術平均數」的優缺點為何?
複習完「眾數」、「中位數」、「算術平均數」,並且搭配例題練習之後,接下來我們要來學習「加權平均數」與「幾何平均數」。其中「加權平均數」相信同學們並不陌生,因為這是用來計算學期成績的方式,我前面也有以此來說明期望值為「平均」的概念。
另一方面,「幾何平均數」通常用來計算變化率的平均值。舉個例來說吧,假設某公司去年的營業額比前年成長60%,而今年的營業額比去年衰退60%,那麼這兩年平均成長率是多少?
如果用算術平均數的概念來寫:[60%+(-60%)]÷2=0,然後將其解讀為持平,這樣是合理的嗎?
事實上,今年的營業額為(1-60%)(1+60%)=64%,營業額剩下了原本的64%,顯然已經衰退了。
那麼應該如何計算呢?假設平均成長率為r,則(1+r)(1+r)=(1-60%)(1+60%),
r=「(1-60%)(1+60%)開根號」再減1
按照這樣的想法,我們可以寫成以下一般的形式:

以下是關於「加權平均數」與「幾何平均數」的教學影片,可觀看學習:
「百分位數」與「四分位數」
「百分位數」原本是國中舊課綱國三的課程,現在是高中108課綱加進來的內容,可以想成是「中位數」概念的推廣。試回想,什麼是中位數呢?
中位數就是將數據分成兩等分,其中「中位數」為其等分點:
至少有50%的數據小於或等於中位數,且至少有50%的數據大於或等於它。
那麼百分位數,就是將數據分成100等分,其中有99個等分點,依大小順序排列:P1、P2、P3、…、P99
其中Pk稱為第k百分位數,k為介於1與99之間的整數。
至少有k%的數據小於或等於Pk,且至少有(100-k)%的數據大於或等於Pk。

因此第k百分位數的計算方式如下:

可搭配以下影片,做幾道例題會更清楚喔:
接下來我們來介紹「四分位數」,顧名思義,就是將數據四等分,其中有三個等分點Q1(第一四分位數)< Q2(第二四分位數) < Q3(第三四分位數);也就是說,Q1=P25、Q2=P50、Q3=P75,其中Q2就是中位數。
變異數與標準差
以上,我們已經介紹完用以代表整體數據「集中程度」的「均量」,接下來我們來介紹用以量化整體數據「分散程度」的「差量」。我們在國中學過的差量為「全距」與「四分位距」。到了高中階段,我們要來介紹「變異數」與「標準差」。這兩個統計量的定義方式如下:

首先,觀察到「變異數」為「標準差」的平方。
為什麼要這樣定義?
既然我們要看數據的分散程度,所以將每個數據與算術平均數比較,計算其差值(此稱為離均差),並將個別數值相加。但是如此就必須處理絕對值的代數運算,這是比較麻煩的。因此,我們改將每個差值平方後再相加。
為了避免數值太大,我們將此n個數值平均。即為變異數。將變異數開根號,則為標準差。
另外,要提醒同學的是,除了要記熟「變異數」與「標準差」的原始公式之外,也要知道它們展開後的形式:

其推導方式如下:

推導方式不難,就是使用乘法公式,以及觀察到「算術平均數」×「總次數」=總和
建議同學,一定要試著將書蓋住,自己獨立推出公式。會推導的好處是,一方面可以記得比較熟,另一方面是萬一忘了可以自己再推出來。
以下是網路上現有的解說影片,同學不妨參考學習。
試試以下這題:數乙106年多選7

這是一道不錯的練習題,首先我們先依據題目將條件列出:

選項(1),只要將自然75分、社會80分代入求出平均及標準差即可:

選項(2):與選項(1)一樣,直接將自然、社會兩科成績代入即可。

選項(3):自然、社會兩科成績總和170分。我們考慮一個比較極端的情況,自然100分,社會70分,如此會造成標準差超過5分。

選項(4):同樣的,我們考慮一個較極端的情形,自然與社會皆滿分,則標準差會超過5分。

選項(5):這是正確的,因此要證明,不能舉例子。

數據的伸縮與平移
老師提問:如果將原本的數據經由「伸縮」與「平移」之後,那麼「算術平均數」及「標準差」會如何變化呢?會考慮這個問題的原因是,有時候我們採用不同的單位來描述同一組數據,那麼不同單位對於「平均數」及「標準差」將造成什麼樣的影響,便是一個很自然的問題。

在推導這個結果之前,我們可以先感覺一下:如果有2個數,分別是1,3,那麼其平均數為2,標準差為1。
現在同乘以2倍加上1,則平均數與標準差會如何改變呢?同學應該可以很容易看出來,平均數變為原來的2倍再加1,而標準差變為原本的2倍。也就是說,加減多少,對於標準差是不會有影響的。
數據標準化
給定任何的數據,都會對應到一組「算術平均數」及「標準差」。為了讓不同數據易於比較,我們可以做一個特殊的伸縮及平移變換,使得這些數據的「算術平均數」及「標準差」一致。其變換方式如下:

不難驗證,經由這樣的變換,所有數據的算術平均數均變為0,標準差均變為1。
關於此結果的推導方式,可觀看以下影片學習:(0~8:50數據的伸縮及平移變換;8:51~數據的標準化)
二維數據分析
前面我們介紹了一維數據分析的「均量」及「差量」,伸縮及平移、標準化數據。接下來我們要來介紹二維數據分析。顧名思義,一維數據分析是針對一組數據(的均量及差量)進行分析;而二維數據分析,則是針對兩組數據的關係進行分析。
用來量化兩組數據關係的量稱為「相關係數」,而「迴歸直線」則是用來預測兩組數據走向的工具。
相關係數
兩組資料的相關性可以分為以下三種:正相關、零相關、負相關。
而「正相關」或「負相關」又可依據其相關程度區分為:完全相關(理想狀態)、高度相關、中度相關、低度相關。我們可以用「散布圖」來觀察兩組資料的相關性,但不夠客觀。也不精確,因此採用「相關係數」進行量化。
相關係數的定義方式如下:

為什麼是這樣定義呢?我們可以畫出一條橫軸及縱軸,通過座標:(x的算術平均數、y的算術平均數)
分子的部份可以度量資料分散在1、3象限多一點,還是2、4象限多一點?然後我們將這一個數字取平均值(除以n),接著再除以x與y的標準差,如此可以使該值落在區間 [-1, 1]。
另一方面,這樣做的好處是,可以減少不同測量單位的數據對圖形的影響,也使圖形分布更加明顯。
為了讓公式易於記憶,我們可以將其改寫成以下形式:

其中
有時候為了計算方便,也可以寫成展開後的樣子:

相關係數在計算上,要善用伸縮與平移的技巧:

關於相關係數的定義,可參考以下教學影片:
迴歸直線
在散佈圖上,我們可以觀察到數據分佈的情形。一般來說,這些資料都不會落在同一條直線上,但是,我們可以針對每一組數據,找到一條直線,使得這些點與這條直線的「鉛直線段長度」平方和為最小。這樣的一條直線,稱為「最佳直線」或「迴歸直線」。寫出的形式如下:

在推導這個公式之前,我們可以先觀察,這條直線必定通過x、y的算術平均數。但是那個斜率為什麼會長成那樣呢?這就得透過最小平方法,經由配方看出來。當然如果會一點微積分,可以簡化不少計算。
建議初學者不用急著推導公式,可以先從演練題目,將公式記熟後,再回來學習如何推導。我認為對於準備考試來說,這是比較有效益的做法。
以下影片是關於迴歸直線的介紹與推導:
第四章 三角比的性質與應用
三角比是高中數學的重頭戲,是人們為了做測量而發展出來的一門學問。如今,三角比已廣泛應用在許多科學領域,例如航空、建築、工程、航海、測繪學…等。
簡單來說,三角比是一個關於角度的函數,用來表示n邊形的邊角關係。包括了「正弦函數」、「餘弦函數」、「正切函數」、「餘切函數」、「正割函數」、「餘割函數」。而且這六個三角函數之間有著特別的關係,稱為三角恆等式。
首先,我們先來問一個問題,既然三角函數是探討n邊形的邊角關係,那為何要叫做「三角函數」,而不叫做「四角函數」、「五角函數」或「六角函數」…?
試想想,任意的多邊形,是不是可被切割成更小的單元?沒錯,那個更小的單元就是三角形。因此,如果我們可以掌握三角形的邊角關係,就可以以此為基礎探討多邊形的邊角關係。
然而,三角形有各式各樣的形狀,其邊角關係還是相當複雜,因此我們將其切割成更小的單元,簡化其邊角關係。那個更小的單元,就是直角三角形。
因此,我們針對直角三角形定義其邊角關係就單純許多了。
銳角三角比的定義

以上符號sin、cos、tan分別為sine、cosine及tangent的縮寫。由於螺旋式的課程架構,另外三個三角函數cot(餘切)、sec(正割)、csc(餘割),要留待之後的課程才會介紹。
對於108課綱的安排,歡迎參考我整理的另一篇文章:高中數學108課綱「課程」與「考試」分析、各版本整理及考生的因應方式
為什麼會取這樣的名稱呢?理由很簡單,會叫做弦,就是與圓的弦有關;會叫做切,就是與圓的切線有關;會叫做割,就是與圓的割線有關。不妨參考以下的影片說明:
有了定義之後,可以練習寫下特殊角(30度、45度、60度)的三角比試試:
提問:15度、75度、18度、22.5度的三角比要如何求呢?
三角比的基本關係式
銳角三角比的關係式有以下幾種:餘角關係、平方關係、商數關係,依課本內容只有以下三種

相信很多老師教到這段應該會很不自在,有一種沒有把事情講完的缺憾。因為只介紹三個三角函數,所以一些關係式便無法呈現出來。
因此,有興趣知道較完整內容的同學可參考以下影片
三角測量(平面、銳角)
這個部份,我們要來介紹,使用三角比來解決測量問題。事實上,就是因為有測量的需求,三角學才得以蓬勃發展。例如:古代埃及測量金字塔高度、或是天文學家使用三角學測量地球的大小,進而繪製成地圖。
在此補充一點,我們中學所接觸的三角學,主要在歐氏空間上(曲率為0)討論,事實上,曲面上的三角學提供了更一般的理論架構,在數學的其中一個分枝「微分幾何」會有較詳盡的說明。
在處理三角測量的問題時,必須先依題意描繪圖形,再使用三角學理論進行計算。因此,將「文字」化為「圖形」是不少學生初學時會遇到的困難,尤其在面對空間圖形時更為明顯(學生容易於平面與空間圖形上造成混淆)。
做測量問題之前,要先知道相關術語如下:
仰角與俯角、方位
觀察高處目標時,視線與水平線的夾角,稱之為「仰角」;
觀察低處目標時,視線與水平線的夾角,稱之為「俯角」。
方位:東、西、南、北、東30度北,西70度南,東北、西南、…。
廣義角三角比與極坐標
廣義角是什麼?
至目前為止,我們考慮的角度介於 0^{\circ}\sim 180^{\circ},並且僅定義銳角的三角函數並考慮其性質。接下來我們要將角度的概念進行推廣。
試想想,角度是如何產生的?相信大家都有坐過摩天輪的經驗,隨著時間推移,摩天輪會緩緩轉動,你要如何描述自己所在的位置呢?
是不是從上車處當作起始點,然後看看「轉」了多少?另外,摩天輪可以「逆時針旋轉」或是「順時針旋轉」。
從摩天輪的例子不難想像,旋轉角度不受限於 0^{\circ}\sim 180^{\circ},並且可以有方向性。這就是我們推廣角度的方法。
如下圖所示:

旋轉時,必須先固定一邊 OA,稱為「始邊」,接著可以依逆時針方向旋轉(如圖(a)),或是依順時針方向旋轉(如圖(b))。根據定義,依逆時針方向旋轉的角度為「正的角度」;依順時針方向旋轉的角度為「負的角度」。這個定義容易理解,我們可以想成,從 OA 出發,一開始往上為「正」、往下則為「負」。
旋轉後停住的邊 OB,稱為「終邊」。
由以上方式定義的角度稱為「廣義角」。
如果兩個角度,其始邊與終邊相等,則稱此兩個角度互為「同界角」。換句話說,如果兩個角度相差 360^{\circ} 的整數倍,那麼這兩個角度便是「同界角」。
看到這裡,可以先做一些基本練習再繼續看下去,
為了可以清楚描述角度並定義三角函數,我們將角的始邊放在 x 軸的正向上,而角的終邊可能落在第一、二、三、四象限,此時這個角分別稱為第一、二、三、四象限角。如果終邊恰好落在 x 軸或 y 軸上,則此角度稱為「象限角」。
如何定義廣義角的三角比?

如上圖所示,在終邊上,任取一點異於原點 O 的點 P(x,y),並且通過 P 點作 x 軸的垂直線,設垂足為 Q,此時 x與 y 分別表示 \Delta OPQ 的鄰邊與對邊。要特別注意的是,x, y 會隨著不同象限而有不同的正負號,而斜邊 r=\sqrt{x^2+y^2} 恆為正。
有了以上的設置,接著就可以去定義各三角比了:
sin{\theta}=\frac{y}{r}, \ cos{\theta}=\frac{x}{r}, \ tan{\theta}=\frac{y}{x}
三角函數雖然有很多公式,但我認為最重要的是定義。只要定義清楚了,很多的公式都可以輕易推出來。因此學習三角函數的過程,基本動作就是熟記定義以及推導,並且記憶一些基本公式。另外一些較為特殊的公式,不必強迫自己一定要記下來。當然對於記憶力特好的人,能記起來當然也是不錯啦。
接著我們來看看廣義三角比有哪些性質。
三角比的性質
從歐幾里德的風車證法看「餘弦定理」的幾何修正項
課程回顧
八年級時,我們第一次學到了「畢氏定理」,這個定理告訴我們,一個直角三角形的兩股平方和等於斜邊的平方。文獻上記載,畢氏定理有超過三百多種的證明方式。其中,歐幾里德的風車證法堪稱經典。到了高一下學期,我們學到了三角比的應用之一:「餘弦定理」。這一篇文章,我們要從風車證法中,觀察餘弦定理修正項出現的原因。雖然證明過程相較課本教我們的方式複雜一些,也沒有這麼直觀,但卻更可以看出餘弦定理修正項與幾何的連結。
畢氏定理的證明方法:歐幾里德的風車證法
首先,我們考慮以下這個圖形:
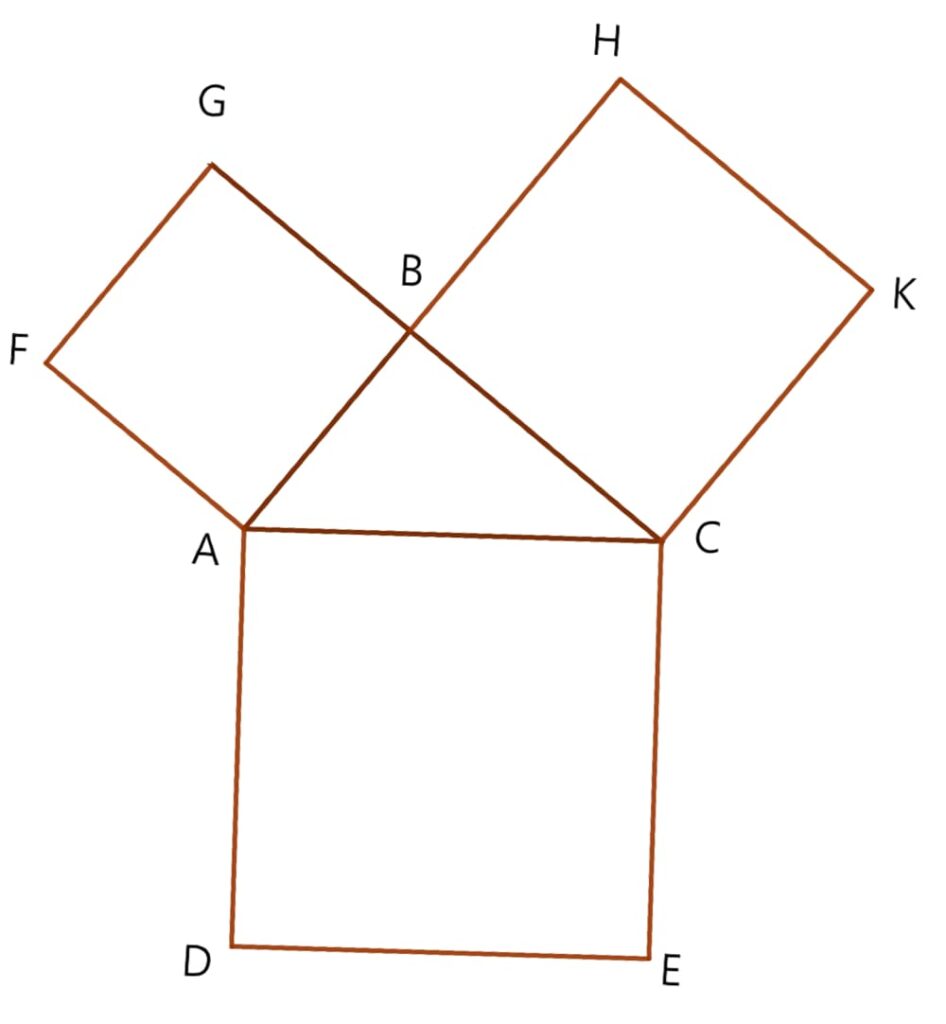
其中\Delta ABC為直角三角形,且 \angle{ABC}=90^{\circ},以其三邊長往外延展出三個正方形 ABGF、ACED、BCKH。
連接CF、BD,並且過B點做鉛直線,分別交\overline{AC}與\overline{DE}於I、L兩點(如下圖)。

稍微觀察一下,不難發現 \Delta ACF \cong \Delta ADB (SAS),先來計算 \Delta ABD的面積

\begin{aligned} \Delta ABD面積 &= \overline{AD}\times h_1 \times \frac{1}{2} \\ &= 矩形ADLI的面積 \times \frac{1}{2} \end {aligned}
另一方面,計算 \Delta ACF的面積
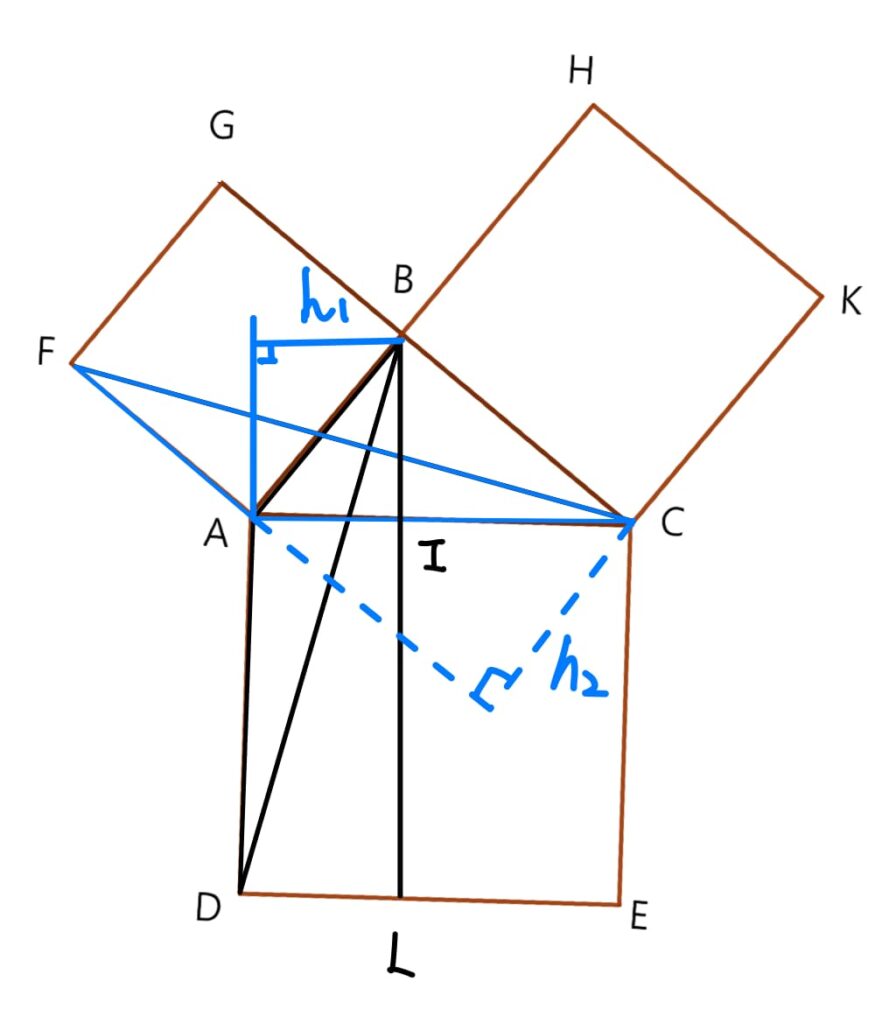
\begin{aligned} \Delta ACF的面積 &= \overline{AF}\times h_2 \times \frac{1}{2} \\ &= 正方形ABGF的面積 \times \frac{1}{2} \end {aligned} 因為 \Delta ABD面積\cong \Delta ACF的面積,所以 矩形ADLI的面積 = 正方形ABGF的面積
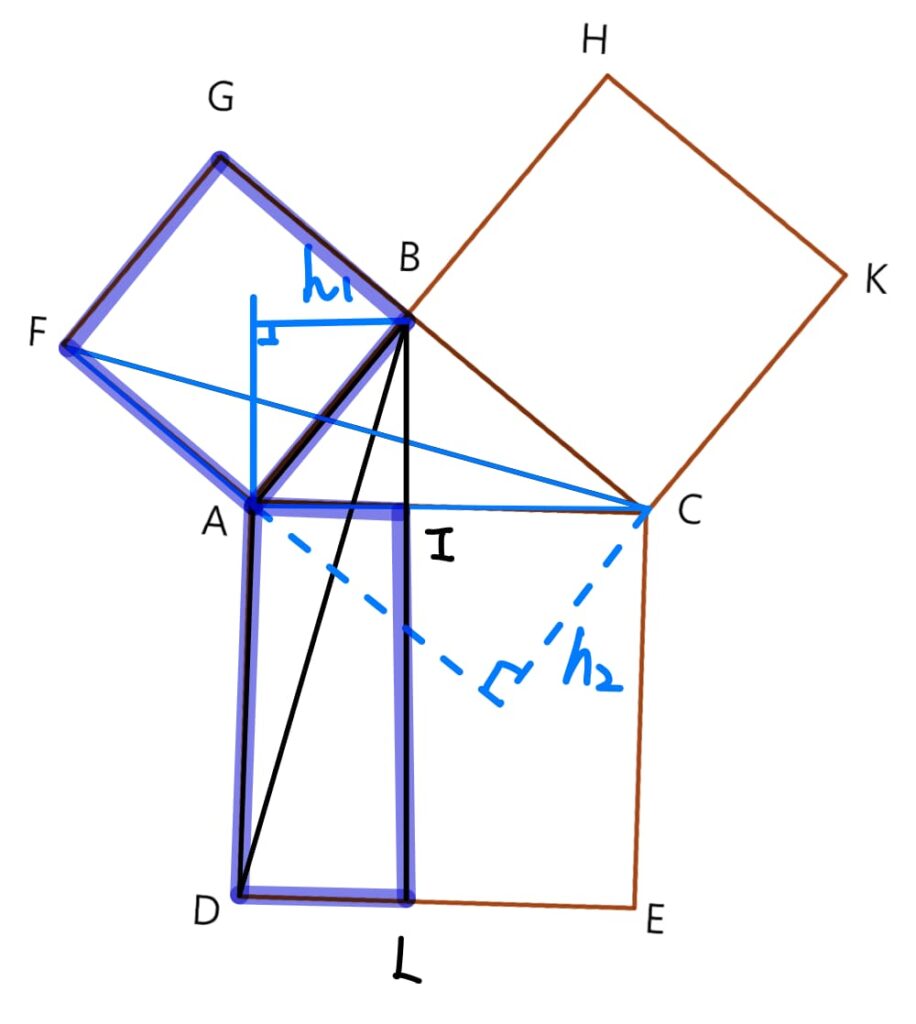
同理,矩形ILEC的面積=正方形BCKH的面積

因此,
\begin{aligned} 正方形ADEC的面積 &= 矩形 ADLI的面積 + 矩形ILEC的面積 \\ &= 正方形ABGF的面積 + 正方形BCKH的面積 \end{aligned} 亦即 \overline{AC}^2=\overline{AB}^2+\overline{BC}^2 得證。
回顧課程:餘弦定理
什麼是餘弦定理?敘述如下:在 \Delta ABC 中,\angle A, \angle B,\angle C 的對邊長分別為 a,b,c,則
\begin{aligned} a^2 &= b^2+c^2 -2bccosA \\ b^2 &= a^2+c^2 -2accosB \\ c^2 &= a^2+b^2 -2abcosC \\ \end{aligned}
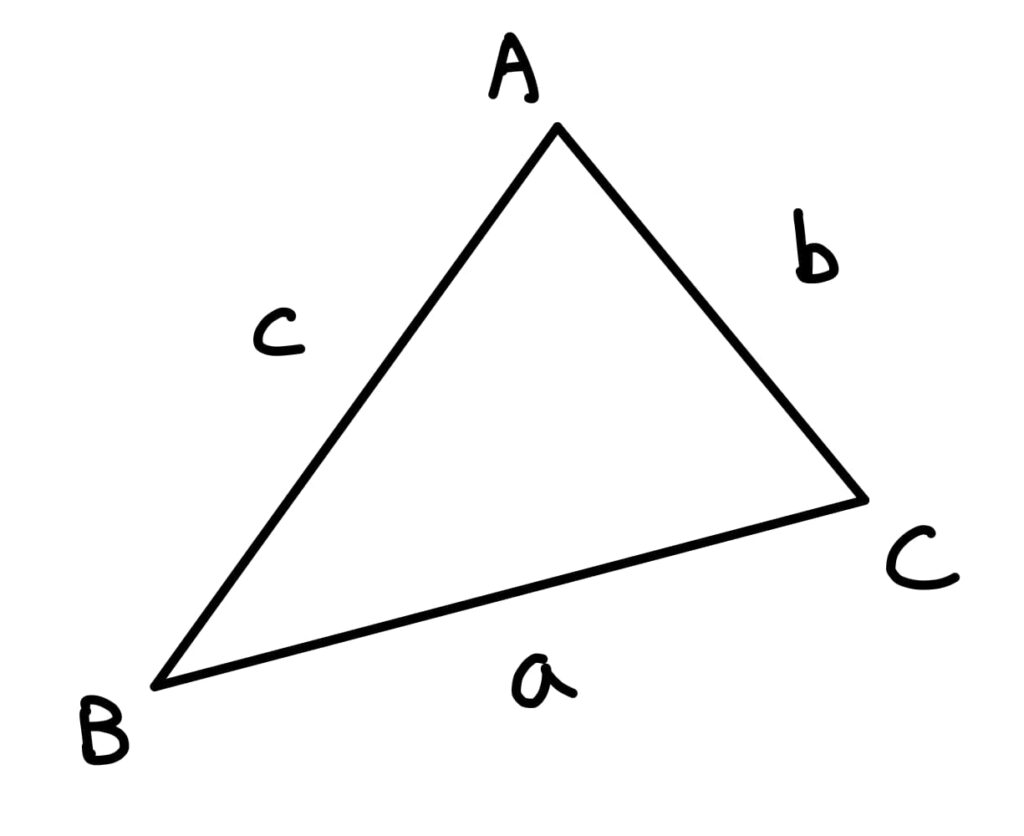
目前教科書提供的證明,主要為代數操作,快速地來複習一下:
第一個方法,作BC 邊上的高 \overline{AD}。
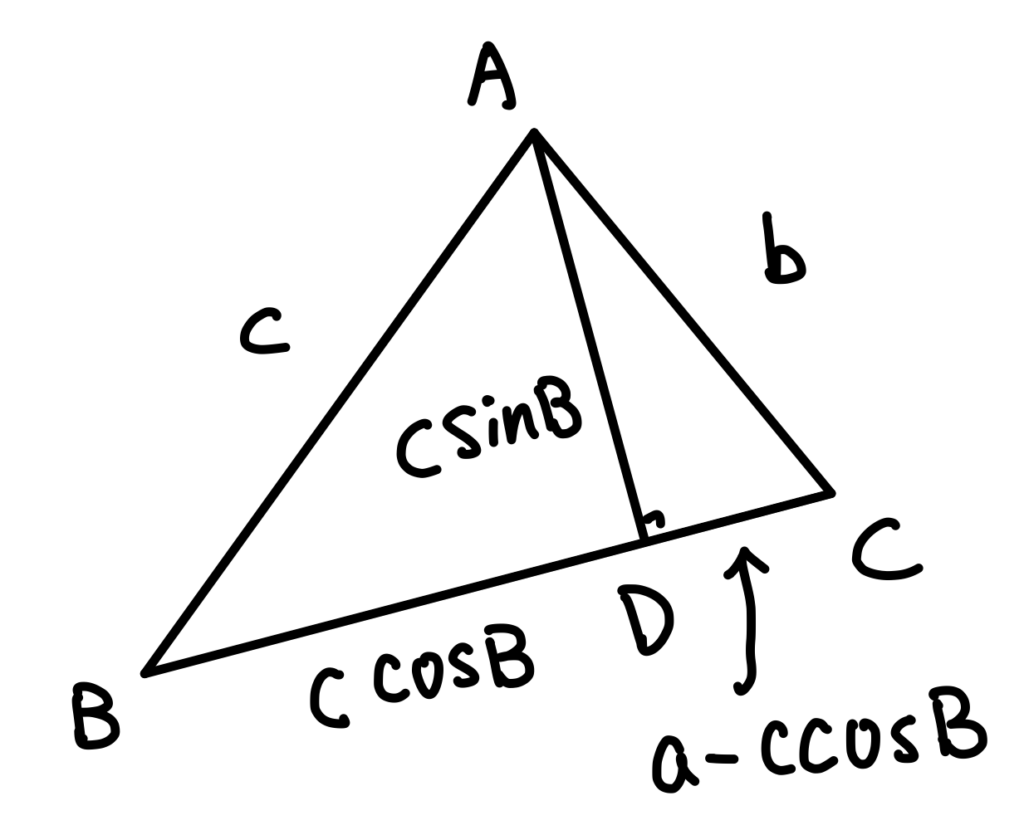
在 \Delta ABD中,\overline{BD}=ccosB, \overline{AD}=csinB,
因此,在\Delta ACD中,\overline{CD}=a-ccosB,根據畢氏定理
\begin{aligned} b^2 &= (a-ccosB)^2+(csinB)^2 \\ &= a^2+c^2-2accosB \end{aligned} 這是很簡單的代數證明。
另一個方式則是使用解析幾何,建立坐標系:以 B 為原點,\overleftrightarrow{BC} 為 x 軸。

標上3個頂點坐標後,寫出 A、C兩點的距離
\begin{aligned} b^2&=\overline{AC}^2 \\ &=(a-ccosB)^2+(csinB)^2 \\ &= a^2+c^2(cos^2B+sin^2B)-2accosB \\ &= a^2+c^2-2accosB \end{aligned}
從以上兩個證明,我們可以看出,餘弦定理的本質其實還是畢氏定理,修正項在代數運算的過程中自然出現了。接下來我們來看看歐幾里德的風車證法中,修正項的幾何意義。
餘弦定理的證明方法:歐幾里德的風車證法
考慮 0^{\circ}<\angle{B}<90^{\circ} (\angle{ABC}>90^{\circ}的情形留給讀者練習),如下圖所示:
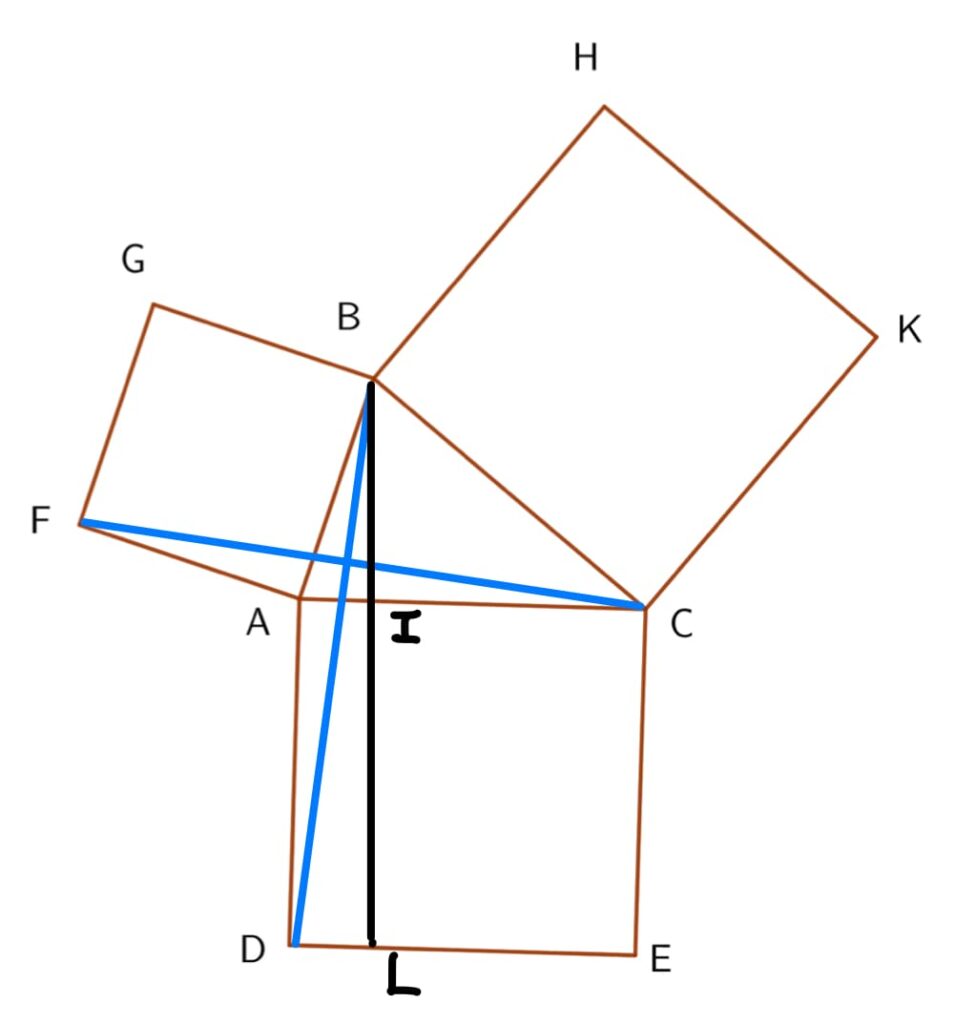
顯然,\Delta AFC \cong \Delta ABD (SAS)。
接著,分別計算 \Delta AFC 及 \Delta ABD 的面積
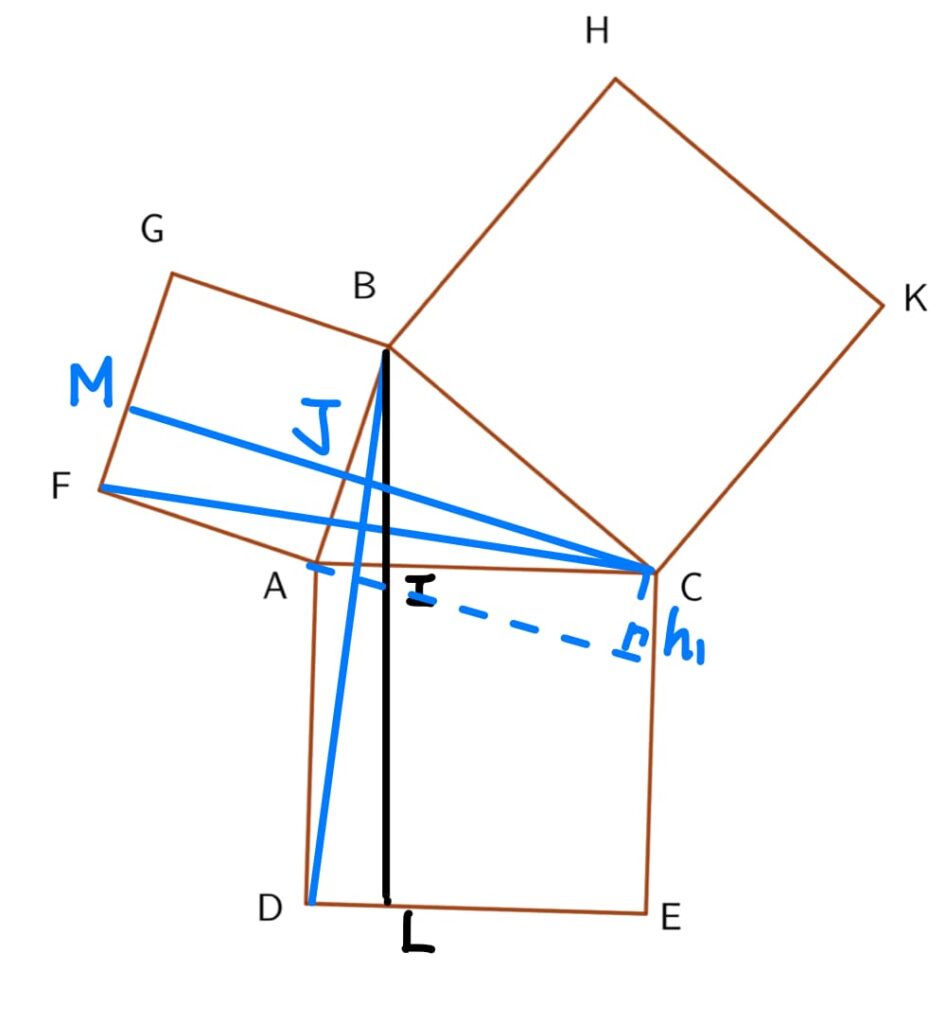
\begin{aligned} \Delta AFC的面積 &= \overline{AF}\times h_1 \times \frac{1}{2}\\ &= 矩形 AFMJ的面積 \times \frac{1}{2} \end{aligned} \tag{1}
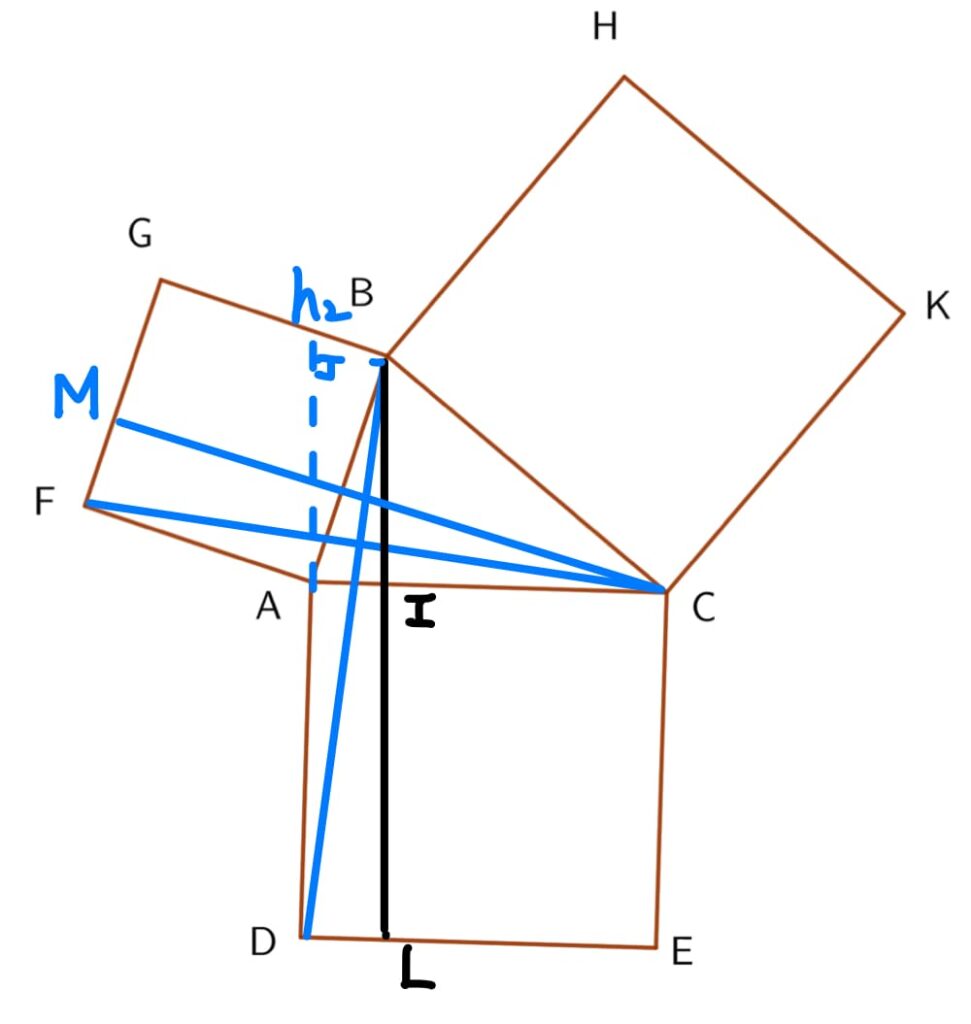
\begin{aligned} \Delta BAD 的面積 &= \overline{AD} \times h_2 \times \frac{1}{2} \\ &= 矩形ADLI的面積 \times \frac{1}{2} \end{aligned} \tag{2}
因為 \Delta AFC \cong \Delta ABD (SAS),所以由第(1)式及第(2)式可知,矩形AFMJ的面積 = 矩形 ADLI的面積
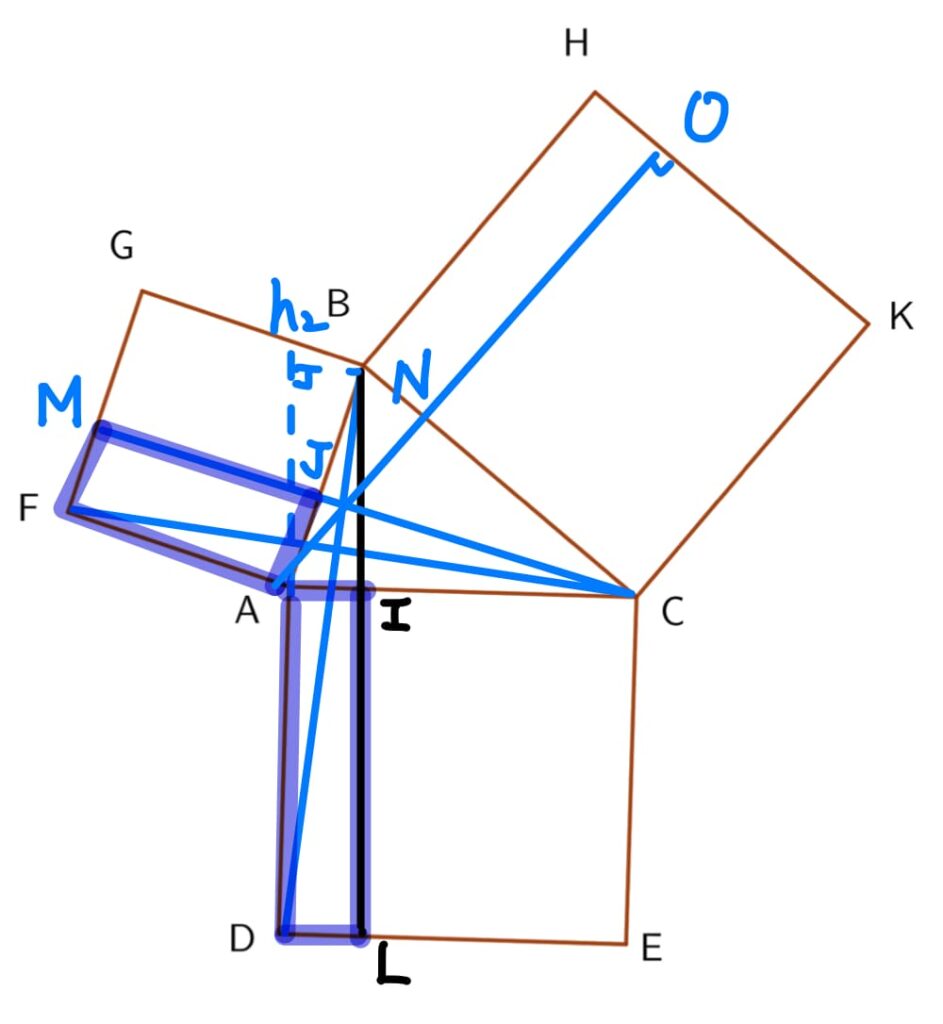
同理,矩形CNOK的面積 = 矩形 ILEC的面積

從這裡可以看出,修正項就是指矩形BJMG及矩形BNOH的面積,其中
矩形BJMG=\overline{BG}\times\overline{BJ}=c\times acosB (如下圖,在\Delta BCJ中,\overline{BJ}=acosB) 矩形BNOH=\overline{BH}\times\overline{BN}=a\times ccosB (如下圖,在\Delta ABN中,\overline{BN}=ccosB)
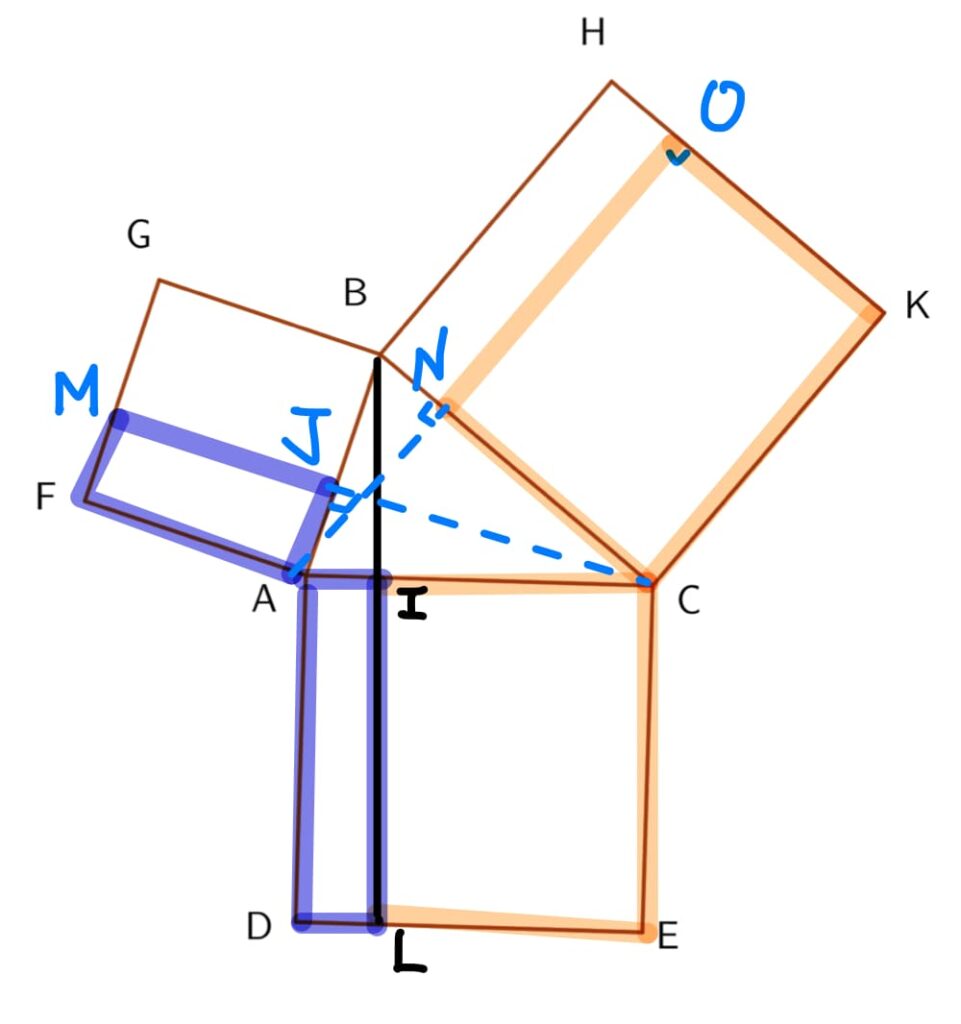
\begin{aligned} \overline{AC}^2=正方形ADEC的面積 &= 矩形ADLI的面積+矩形ILEC的面積 \\ &= 矩形AFMJ的面積+矩形CNOK的面積 \\ &= (正方形ABGF的面積-矩形BJMG的面積)\\ &+ (正方形BCKH的面積-矩形BNOH的面積)\\ &= (\overline{AB}^2-\overline{BC}\times\overline{AB}\times ccosB) + (\overline{BC}^2-\overline{BC}\times\overline{AB}\times cosB) \\ &=\overline{AB}^2+\overline{BC}^2 -2\overline{BC}\times \overline{AB}\times cosB \end{aligned} 證畢。
餘弦定理我已經教了數十次,第一次看到這個證明,覺得很新鮮也很有趣。教科書的編排,往往是以學生容易學習與理解為主,不一定按照歷史脈絡與呈現當初數學家的原始思想,因此我時常鼓勵學生多閱讀課外書籍,不僅是為了考試,而是學習到知識的本質與內涵。
然而,在繁重的課業之下,大多數學生很難有時間閱讀整本書籍,因此採用單篇文章的形式,盡量以淺顯白話的方式書寫,方便學生們閱讀。


