高一數學第1冊(108課綱)-數位教材＋網路資源整合，適合學生自主學習

高中數學數位教材

hi，歡迎你來到這裡。在這個頁面，我將根據108課綱編寫一套以觀念為主的數位教材，除了有文字的解說，同時搭配網路現有教學資源。讓學生可以自學，觀看影片學習。

整個編寫方式是以部落格的形式呈現，所以盡可能少用符號，多講述觀念。同時還有製作目錄，讀者可以自行點選目錄看你想看的主題。看完後，再按「返回目錄」重新選主題。

另外，這不是單純的高中數學內容，還會加入數學史以及一些延伸題材，目的是不要完全受到課綱的限制，讓有興趣的學生學到該學的內容。

要特別注意的是，這些影片是以108課綱章節的順序選取，但錄製的內容不一定完全符合108課綱的要求，請務必對照課本使用，這只是一個輔助的學習方式，在學校還是要用心聽講，才能學到較完整的知識。

關於108課綱，可參考以下文章：

高中數學108課綱「課程」與「考試」分析、各版本整理及考生的因應方式

如果你想要Step by Step的教學課程，歡迎加入以下電子報，我再視需求決定是否製作相關的教學影片。

這個網站專注於製作與研發數位教材，目前已編寫 高一數學第1冊；高一數學第2冊 免費提供給有需要的人使用。

若想接收關於高中數學線上教學的資訊，可加入以下line@官方帳號

歡迎訂閱 高中數學數位學習電子報

高中數學數位學習電子報訪客

第一冊

第一章 數與式

1-1(上) 有理數與乘法公式

有理數的介紹

這部份的內容包含：有理數的定義、分類與性質(封閉性及稠密性)。

有理數具有加減乘除的封閉性，這是什麼意思呢？有哪些數不具備封閉性？

有理數具有「稠密性」，與之相對的概念是「離散性」。那麼什麼數具有離散性呢？答案是整數，因為兩個連續整數之間找不到第3個整數。

是否任何有理數皆可表示為「小數」？如果答案是肯定的，那會是什麼樣的小數呢？有什麼方法可以快速判斷呢？

乘法公式

高中學的乘法公式只比國中多一些，最主要的兩個為「和的立方」、「差的立方」進而衍生出「立方和」與「立方差」公式。這是很多高一學生感到困難的部份。

1-1(下) 根式運算與實數

無理數的介紹

在實數線上，除了有理數之外還有很多個洞，那些洞就是無理數。

事實上，無理數的數量非常多，甚至比有理數多很多，它同樣具有稠密性！

問題：要如何證明無理數的稠密性呢？

這個問題先放著供讀者思考。

然而，無理數不具有加、減、乘、除的封閉性，你是否能舉得出例子說明呢？這件事情非常容易看出來，可觀看以下教學影片。

線上教學：有理數與無理數的「封閉性」和「稠密性」

另外，無理數是否能化為小數？如果能的話，會是何種小數呢？

線上教學：循環小數和無理數的判定/數與數線

無理數的例子

無理數的形式非常多，例如：圓周率、自然底數e、根號、…

但如果要證明一個數是無理數，通常是不容易的。但有一些數是高中數學可以做到的，例如證明根號2是無理數，只要用反證法就能做到。

如何證明根號2是無理數？

但是如果要證明「圓周率」或「自然底數e (又稱為納皮爾常數)」是無理數則有相當的難度。

e的介紹
根式的運算

因為根式是無理數的一種例子，因此這裡順便來介紹根式的運算方式。

1-2 絕對值

絕對值主要是「距離」的觀念，在國中時我們已經學過絕對值的基本運算。到了高中階段，我們將進一步討論「絕對值方程式」與「絕對值不等式」。

1-3 指數與常用對數

在指數的部份，高中課程會擴展到「有理數」及一般的「實數」。指數擴展後不影響指數律，但這個事實須要證明。其中從有理數擴展至一般實數須要用到極限的概念，因此高中階段會略過此證明。

省略的部份，我之後會在這個網站以獨立一篇文章的方式補足，可參考「數學老師在課堂上來不及告訴你的事」。

在指數的學習上，要注意幾點：

  1. 當指數由「正整數」拓展為「整數」再拓展為「有理數」時，底數應該加上什麼限制？
  2. 要思考為何要那樣定義：當指數為負數時，表示倒數；若指數為一個分數時，表示開方根？
  3. 當指數拓展後，要如何驗證仍然滿足指數律？
    指數律與對數表

在「對數」的部份，新課綱已弱化僅討論底數為10的對數。這種對數我們稱之為常用對數。以下線上教學大多還是舊課綱有討論一般底數的情況，可提供學生做為課後補充使用。

第二章 直線與圓

2-1 坐標平面與直線方程式

這一章的重點為直線斜率的意涵、直線方程式的種類、兩直線的關係、點與直線、直線與直線的距離。

直線坐標平面的部份，國中已學過，可參考以下線上教學：

直線斜率的部份：

  • 引出斜率的想法：斜率是量化直線「傾斜方向」與「傾斜程度」的工具。
  • 直線斜率的定義：給定兩點如何求直線斜率？給定一點及斜角如何求出直線斜率？

線上教學：直線方程式-斜率的定義、斜角說明

關於直線方程式的種類：要學習從斜率的定義推導出直線方程式

  • 兩點式、點斜式、斜截式、一般式、點向式、截距式

線上教學：直線方程式的四種型式、2秒鐘背完9種直線方程式

我認為直線方程式最重要的就兩種形式：一般式、截距式。

原因是，一般式是我們代「點與直線」、「直線與直線」距離公式的形式。

因此，如果可以直接將直線以一般式表示，就可以省略掉每次由點斜式化為一般式的移項整理過程。

而截距式方便處理直線與兩坐標軸圍出的三角形區域面積。

線上教學：直線方程式–截距式(理論)、點斜式題目練習+截距式推導

關於兩直線的關係：在平面中兩直線的關係只有三種，分別條列如下

  • 平行
  • 重合
  • 交於一點

其中要注意的事，兩直線平行，則兩斜率相等；兩直線垂直，則兩斜率相乘為負1。要如何證明呢？

線上教學：直線方程式-直線的平行、垂直與斜率的關係說明、兩直線的平行與垂直之經典試題

點與直線，直線與直線的距離

2-2 直線方程式的應用

2-3 圓方程式

我們在高中階段，要開始學習圓方程式，學習的順序如下：

  1. 圓的定義為何？
    圓方程式-圓的定義說明
    圓的方程式
    圓方程式-過三點求圓方程式例題
  2. 圓的方程式有哪些形式？
    圓的標準式
    圓的一般式

2-4 圓與直線的關係

第三章 多項式

3-1 多項式的除法

多項式的基本概念及其運算

綜合除法的注意事項：若除式為ax－b，則操作時，先將除式看成x－b/a，接著會發現商式每一項的係數皆為原本的a倍，要再同時除以a才是以ax－b除完後的商式。

綜合除法範例

餘式定理

餘式定理的精神：可以將除法問題變成求函數值問題；反之，求函數值問題可轉換為除法求餘式。

遇到高次多項式時，餘式定理的精神就是令除式為零，用以降次求餘式。

你可以自己將以上空格填上嗎？或許可以先點選以下連結聽聽解說再決定要怎填較合理。

因式定理

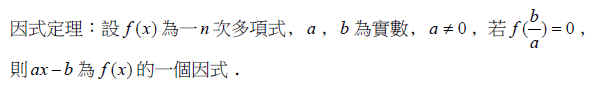
由因式定理可知，一個多項式的因式可與此多項式方程式的根相對應。

3-2 多項式函數

【高中數學探討】三次函數配方法與三次方程式的根式解：數學發現的先後順序之爭

課程回顧

在高中數學第一冊(龍騰版單元10、南一版3-2)提到三次函數的圖形。這一段是108課綱新加入的內容，讓不少學生吃盡苦頭。雖然國中時已經有處理二次函數的經驗，但三次函數複雜許多。

回想一下，我們當初是如何理解二次函數呢？

答案是「配方法」。透過配方，我們可以觀察出來，二次函數，本身是一個「線對稱圖形」。就以一般情況來說吧，考慮一般形式的二次函數$$y=f(x)=ax^2+bx+c$$配方後可寫成如下形式$$y=f(x)=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a}$$ 因此 \(x=-\frac{b}{2a}\) 是此圖形的對稱軸。

然而，三次函數是否也有這樣的對稱性呢？

要回答這個問題之前，首先我們要先嘗試，三次函數是否也可以像二次函數一般「配方」呢？

沒問題，在課本中，就會看到整個配方過程，只是課本可能是以數字演示，而我們以一般的符號呈現如下，整個配方的過程必須熟悉和的立方公式：

$$
\begin{aligned}
y=f(x)&= a(x^3+\frac{b}{a}x^2)+cx+d \\
&= a(x^3+3x^2\cdot\frac{b}{3a}+3x(\frac{b}{3a}))^2+(\frac{b}{3a})^3 + (c-\frac{b^2}{3a})x+d-\frac{b^3}{27a^2}\\
&=a(x+\frac{b}{3a})^3+(c-\frac{b^2}{3a})(x+\frac{b}{3a})+(-\frac{b^3}{27a^2}+\frac{b^3}{9a^2}-\frac{bc}{3a}+d)\\
&= a(x+\frac{b}{3a})^3+p(x+\frac{b}{3a})+f(-\frac{b}{3a})
\end{aligned}
$$

這個配方結果，帶給我們兩個啟發：

第一：此三次函數的圖形對於點 \((-\frac{b}{3a}, f(-\frac{b}{3a}))\) 對稱。

也就是說，對於任何的正數 \(h\)，點 \((-\frac{b}{3a}-h, f(-\frac{b}{3a}-h)) \) 與 點 \((-\frac{b}{3a}+h, f(-\frac{b}{3a}+h)) \) 的中點為 \((-\frac{b}{3a}, f(-\frac{b}{3a}))\) 。課本內容對此性質做了詳細的介紹。

第二：早期的數學家，就是採用這個轉換方式，將三次方程式中的二次項係數消除。也就是說，設 $$y=x+\frac{b}{3a}$$則三次方程式可以改寫為 $$y^3+py=q$$的形式。

這是對於一般三次方程式求解的關鍵步驟。雖然消去三次方程式中的二次項係數不是新鮮事，但是相信有一些學生(包括以前的我)都是直接記下這個變數變換然後代回原本的方程式驗證，高中課本提醒了我們這種變數變換出現的原因。

對於三次方程式的根式解是由誰先寫出來的，在歷史上有過激烈的爭辯。1545年，義大利的醫生兼數學家Cardano在他出版的《大技術》一書中，公開了三次、四次方程式的求解過程。事實上，在他之前，已經有許多數學家對此做了努力。

首先，我們要先知道，這是個對於「負數」的意義都還不太確定的年代。在16世紀時，二次方程式的公式解對於當時的數學家而言是常識。但是一旦遇到根號裡面出現負數，就會被數學家視為無解。這就是我們國中階段所面臨的情況，「二次方程式的判別式小於0，則此方程式無解」。我在國中課堂上，仍然會讓學生知道，更精確得說，不是無解，而是無「實數解」。

在高中時，我們學到了圓與直線的關係，可以用代入消去法，將判斷兩個圖形的交點個數問題轉換為判斷二次方程式解的問題。一旦這個二次方程式出現無(實數)解，就是直線與圓沒有交點的情況。雖然現在看來這不是什麼很難接受的觀念，但在當時，數學家認為這是一種「不真實且虛幻」的情況，一直不想去面對。

就在這樣的年代，可想而知，解出三次方程式是件多麼了不起的事。即使在現代中學的數學課我們也只能解出特殊的三次方程式，並不知道如何推導三次方程式的根式解。

概述三次方程式的求解方法

三次方程式根式解的推導過程，網路上已有很多鉅細靡遺的資料可參考。我試著用口語化的方式，讓讀者更容易理解。

以上已經提到，經過合適的變數變換，可以將三次方程式中的二次項消除，得出以下形式的方程式$$x^3+cx=d$$

Cardano採用幾何證明告訴我們，先找到兩個數 \(u,v\)，使得 $$x=\sqrt[3]{u}-\sqrt[3]{v}$$ 接著，將此數三次方可得
$$\begin{aligned}
x^3=(\sqrt[3]{u}-\sqrt[3]{v})^3 &= (u-v)-3\cdot\sqrt[3]{u}\cdot\sqrt[3]{v}(\sqrt[3]{u}-\sqrt[3]{v}) \\
&= (u-v)-3\cdot\sqrt[3]{u}\cdot\sqrt[3]{v}\cdot x
\end{aligned}$$ 移項整理 $$x^3+3\cdot\sqrt[3]{u}\cdot\sqrt[3]{v}\cdot x=u-v$$ 比較係數可得 $$u-v=d, \ uv=(\frac{c}{3})^3\tag{1}$$ 在第(1)式中，將 \(v\) 代換掉，可得出以下 \(u\) 的二次方程式 $$u^2-du-(\frac{c}{3})^3=0$$

使用二次方程式的公式解，可求得 $$u=\frac{d}{2}\pm\sqrt{(\frac{d}{2})^2+(\frac{c}{3})^3}$$ 看起來雖然有兩個解，但無論代入哪一個，最後 \(x\) 皆相同，如下所示：$$x=\sqrt[3]{\sqrt{(\frac{d}{2})^2+(\frac{c}{3})^3}+\frac{d}{2}}-\sqrt[3]{\sqrt{(\frac{d}{2})^2+(\frac{c}{3})^3}-\frac{d}{2}}$$ 這個公式相較於二次方程式的公式解確實複雜了不少，但還不算太難以記憶。

我們試著解看看以下方程式：$$x^3+6x=20$$

對應到以上公式的符號：\(c=6, d=20\)，接著找到其中一個解如下：$$x=\sqrt[3]{\sqrt{108}+10}-\sqrt[3]{\sqrt{108}-10}$$

可是，數學家邦貝利(R.Bombeli, 1526~1572) 在他的著作《代數學》中提到一個例子：$$x^3=15x+4$$ 他以Cardano的公式代入，得出以下解的形式：$$x=\sqrt[3]{\sqrt{-121}+2}-\sqrt[3]{\sqrt{-121}-2}$$ 在負數的意義還不太確定的十六世紀，這種情形很容易被視為不合理，而將此方程式視為不可解。然而，這個方程式卻可以被分解如下 $$x^3-15x-4=(x-4)(x+2-\sqrt{3})(x+2+\sqrt{3})=0$$ 這個方程式明明是有解的呀！

因此，我們可以猜測，這種三次方根 \(\sqrt[3]{\sqrt{-121}+2}\) 及 \(\sqrt[3]{\sqrt{-121}-2}\) 可以進一步化簡，就如何我們高一做的雙重根式的化簡一樣。

設 $$\sqrt[3]{\sqrt{-121}+2}=a+bi \tag{2}$$ 其中 \(i=\sqrt{-1}\)

將第(2)式等號兩邊同時\(3\)次方可得 $$2+11i=a^3+3a^2bi+3a(bi)^2+(bi)^3=a^3+3a^2bi-3ab^2-b^3i$$ 接著比較實部與虛部：
$$\begin{cases}
a^3-3ab^2=2 \\
3a^2b-b^3=11
\end{cases}$$ 得出 $$\sqrt[3]{\sqrt{-121}+2}=2+i$$ 同樣可得 $$\sqrt[3]{-\sqrt{-121}+2}=2-i$$ 因此 $$x=\sqrt[3]{\sqrt{-121}+2}+\sqrt[3]{-\sqrt{-121}+2}=2+i+2-i=4$$
一旦找到一個實數解，就可以將三次方程式降為二次方程式，接著找到另外兩個根。

此時，我們有個自然的提問：Cardano的公式可以找到其中一個解，那麼其他解要怎麼找呢？

為了不讓這篇文章過多技術性的操作，這裡就先不再詳述推導細節，如果同學有興趣，不妨Google關鍵字，三次方程式，可以找到一大堆資料。

接下來，我們來簡述一下解三次方程式這段有點爭議的歷史。

三次方程式公式解的優先權之爭

對十六世紀的數學家而言，二次方程式的公式解是常識，而三次方程式的公式解則是謀求職業發展與社會地位的秘密武器。

在1510年~1515年之間，義大利波隆大學的數學家費羅(Scirione dal Ferro, 1465-1526)提出了缺二次項的三次方程式 \(x^3+cx=d\)的代數解。當時他並未將此解法公開，而且嚴加保密，直到去世時，才將此解法傳給他的女婿納夫與一個學生費爾(Antonio Maria Fior)。

費爾原本將藉著解三次方程式謀求教職，豈料此時盛傳另一位數學教師塔爾塔利亞(Tartaglia,1499-1557)也會解三次方程式。當時(1535年)他們為此舉辦了一場比賽，比賽方法就是每個人向對方提出三十道題目，在40到50天之內解出最多題目者獲勝。結果塔爾塔利亞大獲全勝，他在2個小時之內就將費爾出的題目全部解出。

後來另一位數學家Cardano聽聞此事，用盡各種方法請求Tartaglia允許他在即將出版的書中披露3次方程式的解法，並承諾會歸功於Tartaglia。Tartaglia當然不願意，但Cardano利用他的贊助者，同時也是米蘭的統治者瓦斯托侯爵之名義，誘使Tartaglia與他碰面。Targaglia最後終於給出了「解法規則」，但是以曖昧不明的詩句形示表示，也沒有對解法的實證。

Cardano在助理Ferrari的幫助下，花了六年的時間，揣摩出那些詩句的意思，又擴展它們的含義，將十三種類型的三次方程式的解法完全呈現在《大技術》這本書中，並且以幾何的方式加以實證，甚至在後面幾章，在助理的協助下得到了四次方程式的公式解。

此書出版後的第二年，憤怒的Tartaglia出版了《新問題與發現》，前半部揭示了他發現的問題的解法，後半部則用來批評Cardano的數學能力及剽竊行為。但Cardano的助理Ferrari駁斥Tartaglia的說法，並且認為Cardano的解法應該歸功於之前的數學家費羅以及費爾才是。一翻論戰後，Tartaglia失去了教職，而Ferrari獲得了波隆納大學的教職。Tartaglia在往後的人生，一心報復Cardano，最後使盡一切手段與陰謀，讓Cardano遭到驅逐，並且破產，入獄，隱姓埋名過完一生。

在課堂上，我們花了很多時間在數學技術上的操作，但是課程安排的順序，未必是歷史發展的方式。當我們試著從歷史的脈絡中認識數學，也許可以從中獲得截然不同的體會。這篇文章就先寫到這邊。如果你對這類主題的文章有興趣，歡迎訂閱「高中數學數位學習電子報」，你會收到相關資訊通知。

歡迎訂閱 高中數學數位學習電子報

高中數學數位學習電子報訪客

3-3 多項不等式

國中時我們已經學過一次不等式，到了高中我們要進一步處理二次不等式及高次不等式。

數學相關議題

小學階段學習奧數：利大於弊，還是弊大於利

站長簡介

你好，我是Gim，一名數學教師，專攻高中數學、大學微積分教學，目前已有二十年教學經驗。教過武陵高中、中大壢中、復旦高中、內壢高中、桃園高中、振聲高中、新興高中、啟英高中、薇閣中學、延平中學、北一女中、…等校學生。協助學生規畫學測、指考複習。

教學方式著重觀念，逐步引導，按部就班，穩紮穩打。

0

高中數學數位學習電子報訪客