歡迎訂閱 高中數學數位學習電子報

訂閱後，可收到高中數學學習相關訊息或課程發佈通知

試題＋簡答下載

前言

這份試題不是很好寫，計算量偏多，要取得高分不太容易。 今年試題各大題的配分與去年試卷相同。第貳部分兩大題配分一致(各有3小題)且各小題之間均有連貫性。其中比較困難的題目分別為多選第6題、選填第11題、計算14題、17題。 以下提供個人的解題淺見，我試著用淺顯白話的方式解說，有需要的同學請自行參考。

單元比重分析

第一冊：22	第二冊：6	第三冊：14	第四冊：14	選修甲(上)：28	選修甲(下)：16
1-1 實數	1-1 數列與數學歸納法	1-1 三角函數的圖形	1-1 空間概念	1-1 隨機變數：多選7	1-1 數列及其極限
1-2 絕對值：多選4	1-2 級數	1-2 三角的和角與差角公式：選填9	1-2 空間向量的坐標表示法	1-2 二項分布與幾何分布	1-2 函數及其極限
1-3 指數：單選2	2-1 一維數據分析	2-1 指數函滿	1-3 空間向量的內積	2-1 複數與多項式方程式	2-1 微分的概念與性質
1-4 常用對數	2-2 二維數據分析	2-2 對數與對數律	1-4 外積、體積與行列式：多選6	2-2 複數的幾何意涵：多選8	2-2 微分的應用：題組13
2-1 直線方程式及其圖形	3-1 基本計數原理	2-3 對數函數	2-1 平面方程式	3-1 拋物線	3-1 積分的概念與性質：單選3
2-2 直線方程式的應用	3-2 排列：選填11	3-1 平面向量的運算	2-2 空間中的直線：選填10	3-2 橢圓：題組15~17	3-2 積分的應用：題組14
2-3 圓方程式	3-3 組合	3-2 平面向量的內積：題組12	3-1 條件機率與貝氏定理	3-3 雙曲線
2-4 圓與直線的關係	3-4 機率	3-3 平面向量的應用 單選1	3-2 貝氏定理與主觀、客觀機率
3-1 多項式的運算與應用	4-1 直角三角形的三角比		4-1 三元一次方程式
3-2 多項式函數及其圖形：多選5	4-2 廣義角的三角比		4-2 矩陣的運算
3-3 多項式不等式	4-3 三角比的性質		4-3 矩陣的應用

題型及試題內容解析

單選1：平面向量與參數式

這一題我們先畫一個簡圖來看一下：

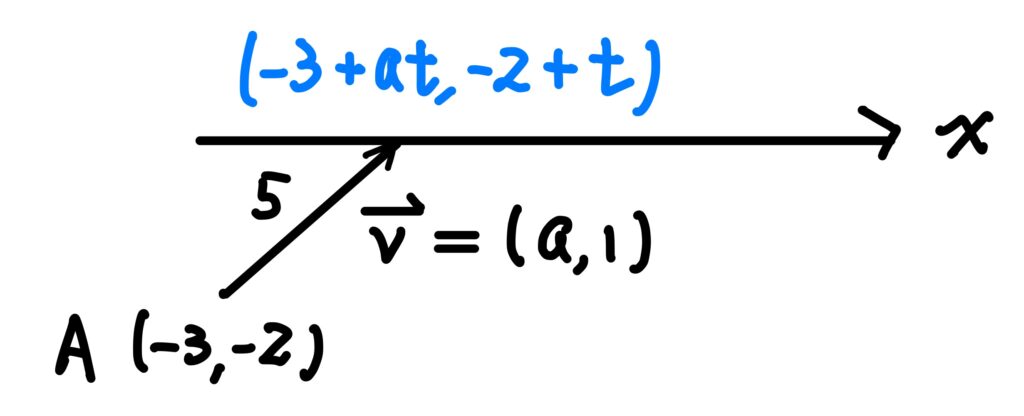
因為點在 \(x\) 軸上，因此 \(-2+t=0\) 解得 \(t=-2\)。

接著計算 \(A\) 點與觸碰到 \(x\) 軸上點的距離：
$$(2a)^2+2^2=5^2$$ 簡單計算一下可得 $$a=\frac{\sqrt{21}}{2}$$ 因此答案選 (4)

單選2：指對數函數的應用

這一題是常見指對數的應用題，沒什麼特別。

假設112天後，物質B與物質A的質量分別為 \(m_B\)與\(m_A\)，依題意列式如下：
$$\frac{1}{4}=\frac{m_B}{m_A}=\frac{(\frac{1}{2})^{\frac{112}{T_B}}}{(\frac{1}{2})^{\frac{112}{T_A}}}=(\frac{1}{2})^{\frac{112}{T_B}-\frac{112}{T_A}}$$
將 \(\frac{1}{4}\) 寫成 \((\frac{1}{2})^2\)，比較指數可得 $$\frac{112}{T_B}-\frac{112}{T_A}=2$$ 因此答案選(2)

單選3：黎曼和與積分

這一題測驗基本的黎曼和表示法，我們可以將式子改寫如下：
$$\frac{3}{n}(\sqrt{4+(\frac{3}{n})^2}+\sqrt{4+(\frac{6}{n})^2})+…+\sqrt{4+(\frac{3(n-1)}{n})^2}$$
這可以理解成函數 \(f(x)=\sqrt{4+x^2}\) 在區間 \([0,3]\) 的黎曼和，取極限後收斂至 $$\int_0^3\sqrt{4+x^2}dx$$
因此答案選 (3)

多選4：絕對值不等式

依照題意，我們可以將各個數的相對位置畫在數線上：

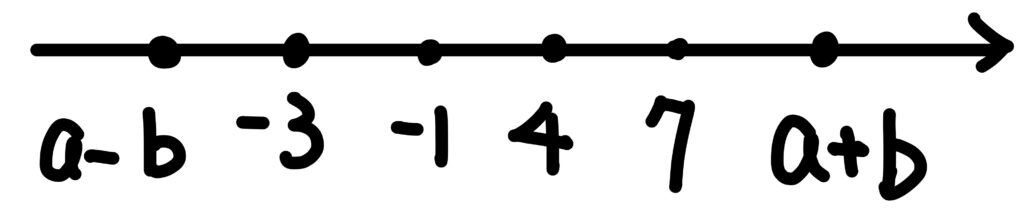
選項(1)：因為 \(-1<\sqrt{10}<4\)，所以\(\sqrt{10}\) 落在區間 \((a-b,a+b)\)內，故此選項正確。

選項(2)：若 \(|x-a|\leq b\)，則 \(|-x+a|\leq b\)，故此選項正確。

選項(3)：若 \(|x-a|\leq b\)，則 $$|\frac{x}{2}-\frac{a}{2}|\leq \frac{b}{2}$$
也就是說，\(-\frac{3}{2}\)，\(-\frac{1}{2}\)、2、\(\frac{7}{2}\)滿足 \(x\) 的不等式 $$|x-\frac{a}{2}|\leq\frac{b}{2}$$
故此選項錯誤。

選項(4)：若 \(b=4\)，則 $$(a+4)-(a-4)=8<7-(-3)$$
也就是說，區間\( (a-b,a+b) \) 不可能同時包含 \(-3\) 與 \(7\) 這兩個數字。故 \(b\) 不可能等於 \(4\)。

選項(5)：若 \(a=b\)，則在區間 \((0,2a)\) 中不可能同時包含 \(-3, -1, 4, 7\) 這四個數，如下圖所示：

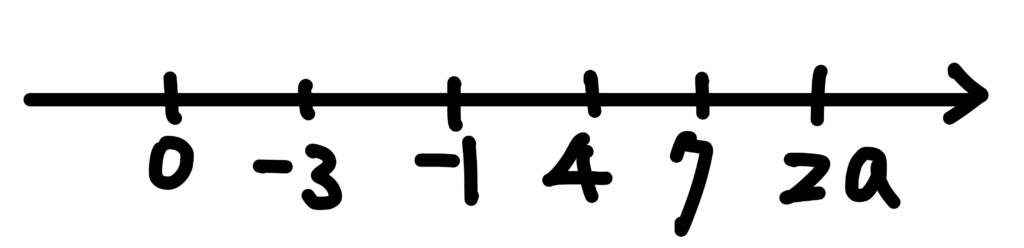
故此答案不正確。最後答案選(1)(2)

這一題相對簡單。

選項(1)：因為此多項式方程式 \(f(x)=0\) 為「實係數」多項式方程式，因此虛根成對，故此選項正確。

選項(2)：因為多項式方程式 \(f(x)=0\) 有兩根 \(1+2i\) 與 \(1-2i\)，因此有因式 \(x^2-2x+5\)。我們做一下長除法如下：

餘式為 \(0\)，故 \(a-12=0\)、\(b+55=0\) 可得 \(a=12, b=-55\)，故選項(2)不正確。

選項(3)：$$f(x)=x^4-4x^4-2x^2+12x-55=(x^2-2x+5)(x^2-2x-11)$$

接著將等號兩邊微分：$$f'(x)=4x^3-12x^2-4x+12=4(x-1)(x-3)(x+1)$$
畫個簡圖看一下：

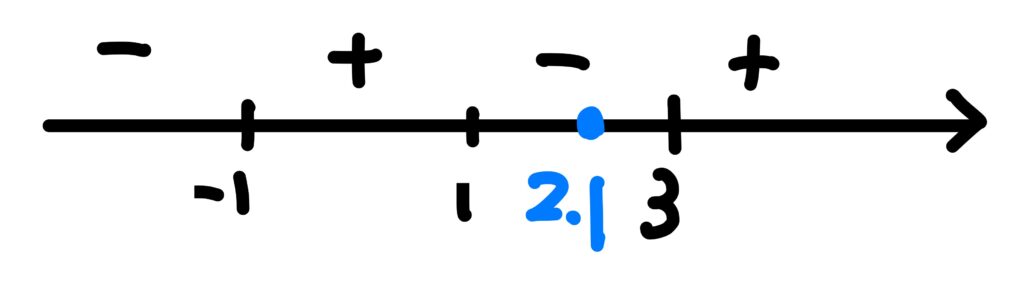
因此 $$f'(2.1)<0$$ 此選項正確。

選項(4)：畫圖觀察函數 \(f(x)\) 的遞增與遞減範圍：

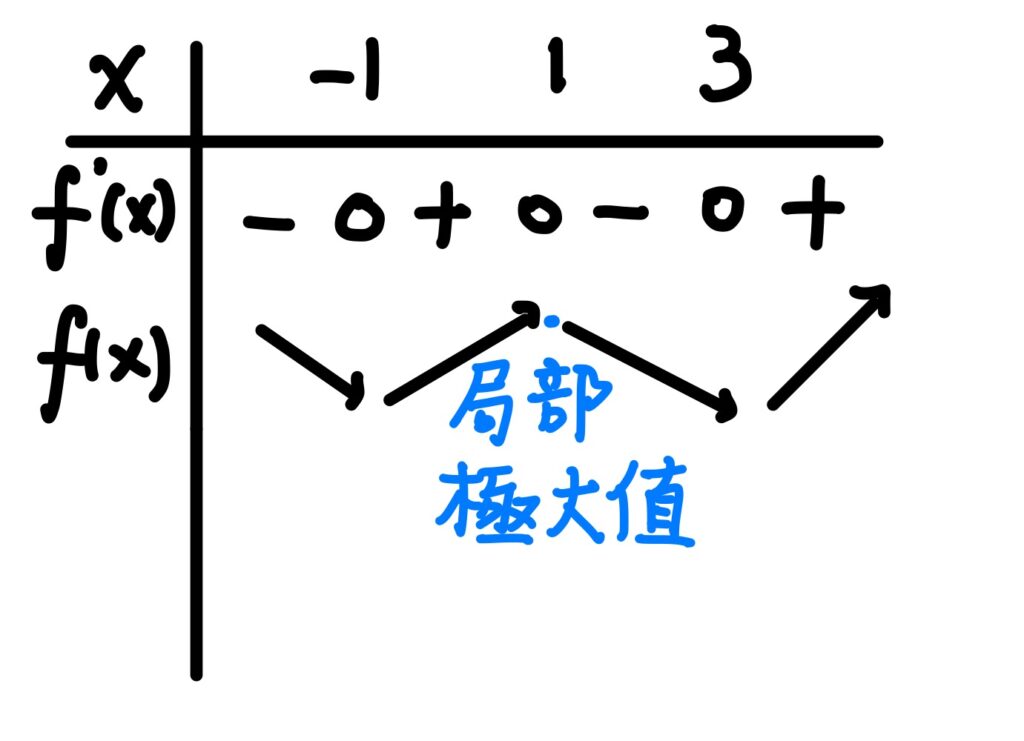
因此函數 \(y=f(x)\) 在 \(x=1\) 有局部極「大」值才對，故此選項錯誤。

選項(5)：要找反曲點，先計算二階導數：$$f”(x)=12x^2-24x-4=4(3x^2-6x-1)$$
\(f”(x)=0\) 的兩根為 \(x=\frac{3\pm\sqrt{12}}{3}\) 一正一負，故此選項錯誤。因此答案選(1)(3)

多選6：三階行列式的幾何意義

這一題不太容易，分析如下：

首先寫下矩陣\(A\)的行列式值
$$detA=tdet\left[\begin{array}{cc}
a & b \\
c & d
\end{array}\right]
$$
選項(1)：因為 \(\vec{u}、\vec{v}、\vec{w}\) 兩兩垂直，故$$|detA|=|\vec{u}||\vec{v}||\vec{w}|\neq 0$$
因此可推論
$$\left|\begin{array}{cc}
a & b \\
c & d
\end{array}\right| \neq 0
$$
因此選項(1)正確。

選項(2)：只需舉個反例即可
$$\vec{u}=(1,2,0)、\vec{v}=(-1,-2,0)、\vec{w}=(2,-1,1)$$
因此選項(2)不正確。

選項(3)：同樣地，可以舉出一個反例 $$\vec{u}=(1,2,0)、\vec{v}=(-1,-2,0)、\vec{w}=(2,-1,1)、\vec{w’}=(2,-1,2)$$
也是說，我們要找到一個向量\(\vec{w’}\) 同時與 \(\vec{u}、\vec{v}\)垂直，但是與向量 \(\vec{w}\) 不平行。

因此選項(3)不正確。

選項(4)：由題意可知 \(detA\neq 0\)，可推論
$$\left|\begin{array}{cc}
a & b \\
c & d
\end{array}\right| \neq 0
$$

用線性代數的說法，就是向量 \(\vec{u}、\vec{v}、\vec{w}\) 線性獨立，則矩陣 \(A\) 滿秩(full rank)，因此可逆，進而可推論其行列式不為 \(0\)。

選項(4)正確。

選項(5)：

因為向量 \(\vec{u}、\vec{v}\) 不平行，且向量 \(\vec{w}\) 同時垂直向量 \(\vec{u}\) 與向量 \(\vec{v}\)，
所以向量 \(\vec{u}、\vec{v}、\vec{w}\) 所張出來之平行六面體體積不為 \(0\)，因此 \(detA\neq 0\)

選項(5)正確，因此答案選(1)(4)(5)

多選7：期望值

這一題題目很冗長，但不算太難。

選項(1)：$$E(X_1)=\frac{1}{2}\times 5 + \frac{1}{2}\times 7 = 6$$ 此選項正確。

選項(2)：投擲銅板兩次回到原點的可能性為一正一負。因此$$P(X_2=12)=(\frac{1}{2})^2\times 2=\frac{1}{2}$$

選項(3)：投擲銅板8次後停留的位置，按次序討論如下：8正(4)、7正1反(6)、6正2反(8)、5正3反(10)、4正4反(12)、3正5反(2)、2正6反(4)、1正7反(6)、8反(8)，不可能停留在5的位置，因此 $$P(X_8=5)=0$$
此選項不正確。

選項(4)：投擲銅板8次棋子移動到4的位置的可能性為：8正、2正6反，故 $$P(X_8=4)=(\frac{1}{2})^8+C^8_2(\frac{1}{2})^8$$

投擲銅板8次棋子移動到8的位置的可能性為 $$P(X_8=8)=(\frac{1}{2})^8+C^8_6(\frac{1}{2})^8$$

因此 $$P(X_8=4)=P(X_8=8)$$此選項正確。

選項(5)：直接計算如下
$$\begin{aligned}
E(X_8) &= (\frac{1}{2})^8[2\cdot C^8_3+4\cdot(C^8_8+C^8_2)+6\cdot(C^8_7+C^8_1)+8\cdot(C^8_6+C^8_0)+10\cdot C^8_5+12\cdot C^8_4] \\
&= \frac{1956}{2^8} > 7
\end{aligned}$$

故此選項不正確。因此答案選(1)(4)

多選8：複數平面

選項(1)：$$\frac{z^3}{4\overline{z}}=\frac{-8i}{-2i}=4$$ 此選項不正確。

選項(2)：將等式兩邊取絕對值：
$$
|\alpha^3| = |4i\overline{\alpha}| \Rightarrow |\alpha|^3 = 4 |\alpha| \Rightarrow |\alpha|(|\alpha|^2-4) = 0 \\
$$

因為 \(\alpha\geq 0\)，所以 \(\alpha=2\)，此選項正確。

選項(3)：$$\frac{\beta^3}{\overline{\beta}}=\frac{(i\alpha)^3}{-i\overline{\alpha}}=\frac{-i\alpha^3}{-i\overline{\alpha}}=\frac{4i\overline{\alpha}}{\overline{\alpha}}=4i$$
此選項正確。

選項(4)：令 \(z=2(cos\theta+isin\theta)\)

$$i=\frac{z^3}{4\overline{z}}=\frac{8(cos3\theta+isin3\theta)}{4\cdot 2(cos(-\theta)+isin(-\theta))}=cos4\theta+isin4\theta$$
因此可得 $$4\theta=2k\pi+\frac{\pi}{2} \Rightarrow \theta=\frac{k\pi}{2}+\frac{\pi}{8}$$
其主幅角的最小可能值為 \(\frac{\pi}{8}\)，此選項不正確。

選項(5)：由選項(4)可知滿足 \(z^3=4i\overline{z}\) 的非零複數 $$z=2cos\theta+2isin\theta$$其中 $$\theta=\frac{k\pi}{2}+\frac{\pi}{8}，k=0,1,2,3 $$ 共有四個。
此選項不正確，因此答案選(2)(3)

選填9：和差角公式的應用

首先我們可以驗證 \(\sqrt{7}^2=\sqrt{3}^2+2^2\)，由畢氏逆定理可知 \(\angle{ACB}=90^{\circ}\)，我們不妨將此圖形座標化：

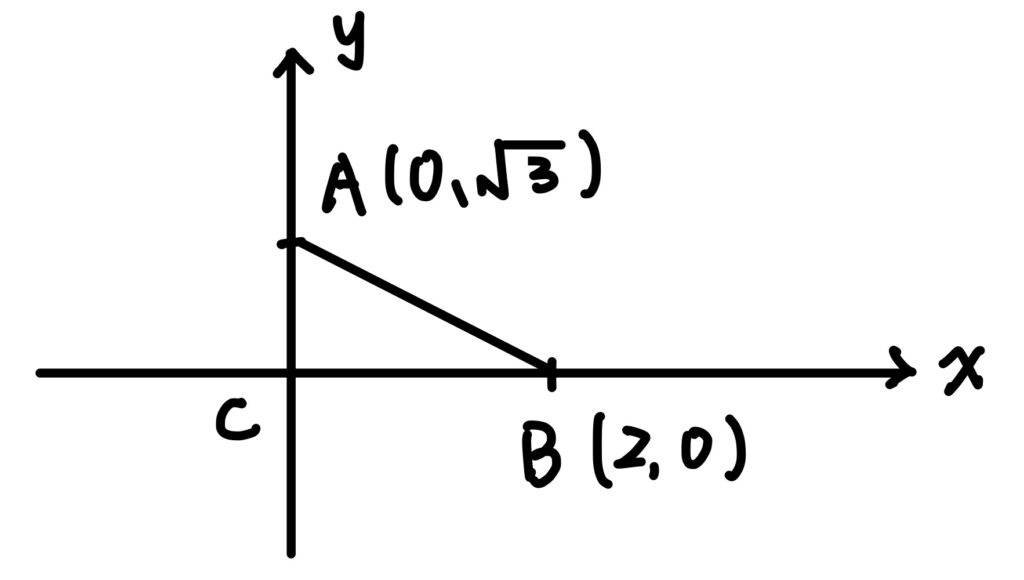
接著依題意，分別畫出頂角為 \(120^{\circ}\) 的等腰三角形 \(\Delta{MAB}\) 及 \(\Delta{NAC}\)如下圖所示：

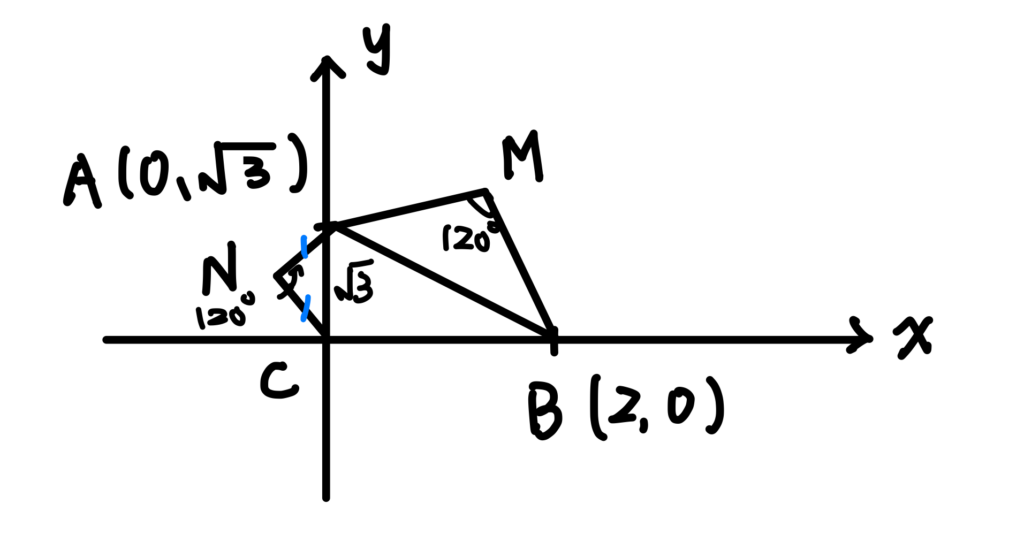
接著可以很快標出點\(N\)的座標 \((-\frac{1}{2},\frac{\sqrt{3}}{2})\)，如果我們可以標出點\(M\)的座標，這一題就差不多

可以解出來了。如下圖，過\(M\)作一條鉛直線交\(x\)軸於\(H\)，並且令\(\angle{ABC}=\theta\)。

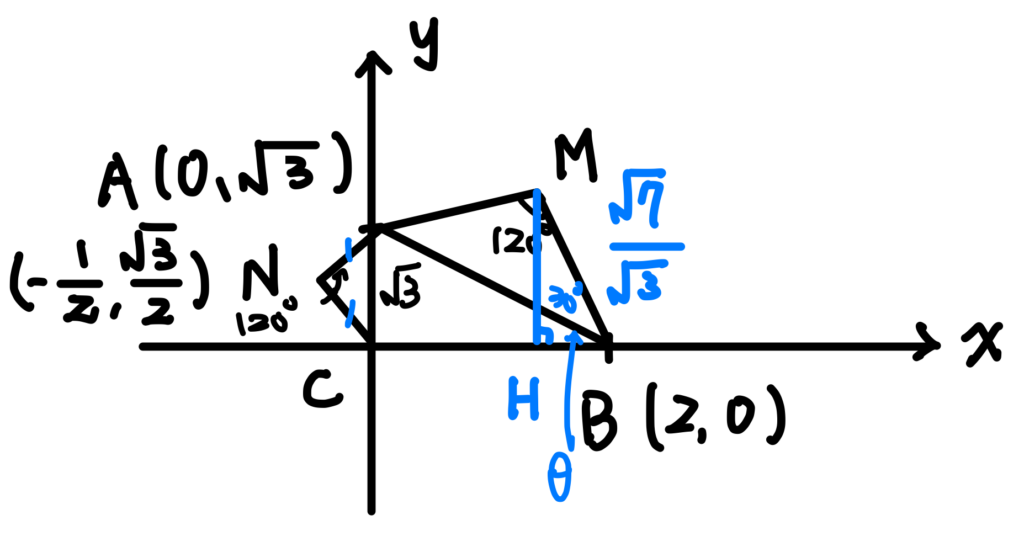
利用和角公式計算 $$cos({30^{\circ}+\theta})=\frac{\sqrt{3}}{2}cos\theta-\frac{1}{2}sin\theta=\frac{\sqrt{3}}{2}\cdot\frac{2}{\sqrt{7}}-\frac{1}{2}\cdot\frac{\sqrt{3}}{\sqrt{7}}=\frac{\sqrt{3}}{2\sqrt{7}}$$
$$sin(30^{\circ}+\theta)=\frac{1}{2}cos\theta+\frac{\sqrt{3}}{2}sin\theta=\frac{1}{2}\cdot\frac{2}{\sqrt{7}}+\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{\sqrt{7}}=\frac{5}{2\sqrt{7}}$$

接著可以標出點 \(M\) 的坐標
$$\begin{aligned}
x 坐標 &= 2-\frac{\sqrt{7}}{\sqrt{3}}\cdot\frac{\sqrt{3}}{2\sqrt{7}}=\frac{3}{2}\\
y 坐標 &=\frac{\sqrt{7}}{\sqrt{3}}\cdot\frac{5}{2\sqrt{7}}=\frac{5}{6}\sqrt{3}
\end{aligned}$$

接著可以計算出線段\(MN\) 的平方：
$$\
\overline{MN}^2 =(\frac{3}{2}+\frac{1}{2})^2+(\frac{5}{6}\sqrt{3}-\frac{\sqrt{3}}{2})^2=2^2+\frac{1}{3} = \frac{13}{3}
$$

選填10：空間中的平面與直線

可以先畫個示意圖看一下：

如圖所示，我們的目標是要算出線段 \(\overline{AB}\) 的長度。首先，通過 \(A\) 對平面 \(E_2\) 作垂直線，設其垂足為 \(H\)。因此
$$\overline{AH}=d(E_1,E_2)=\frac{10-(-4)}{\sqrt{2^2+3^2+6^2}}=2$$ 接著計算向量\(\overrightarrow{AB}\) 與 平面\(E_1\) 法向量的夾角的餘弦值：$$cos\theta=\frac{(1,-2,2)\cdot(2,3,6)}{\sqrt{1^2+(-2)^2+2^2}\sqrt{2^2+3^2+6^2}}=\frac{8}{3\times 7}=\frac{8}{21}$$

故 $$\overline{AB}=\frac{2}{cos\theta}=2\cdot\frac{21}{8}=\frac{21}{4}$$

選填11：排列組合

這一題排列組合有些麻煩，關鍵在於「分類」及「逐情況討論」。這十張卡牌編號如下：$$1,2,3,4,5,6,7,8,8,9$$分類如下：

兩個8：四個位置選2個放數字8，剩下8個數字選2個排列 $$C^4_2\times P^8_2=336$$
大於6400：

情況一：一個8但不在千位數，千位數字可以是9或7。

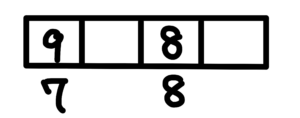
$$C^3_1\times P^7_2\times 2=252$$

情況二：一個8放在千位數，剩下非8的數字有8個，選三個排入另外3個位置。

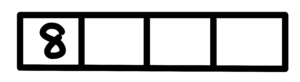
$$P^8_3=336$$

情況三：千位數為6，百位數為9或7或5或4。8有兩個位置可以選，剩下六個數字從兩個位置中選一個，然後有四種情況。

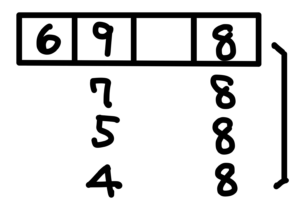
$$C^2_1\times C^6_1\times 4$$

情況3：千位數放數字6，百位數放數字8，剩下7個數字排入兩個位置。

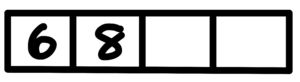
$$P^7_2=42$$

情況4：沒有8，千位數為9或7，剩下七個數選3個排入。

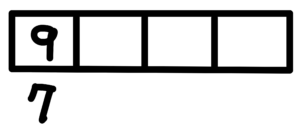
$$P^7_3\times 2 = 420$$

情況5：沒有8，千位數為6，百位為為9或7或5或4，剩下六個數選2個排入。

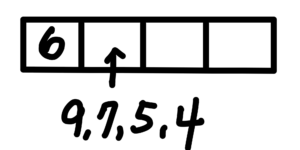
$$P^6_2\times 4=120$$

以上合計：$$336+252+336+48+42+420+120=1554$$

12-14題組

首先可先將 \(a\)、\(b\) 的值：$$\frac{1}{2}=f(1)=a$$ $$1^2+(\frac{1}{2})^2-3\times\frac{1}{2}+b=0 \Rightarrow b=\frac{1}{4}$$

接著寫出圓 \(\Omega\) 的標準式
$$\Omega: x^2+(y-\frac{3}{2})^2=2，圓心 C(0,\frac{3}{2})$$

題組12：兩向量夾角的餘弦值

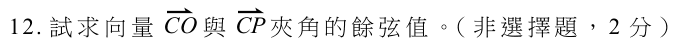
$$cos\theta=\frac{\overrightarrow{CO}\cdot\overrightarrow{CP}}{|\overrightarrow{CO}|\cdot|\overrightarrow{CP}|}=\frac{(0,-\frac{3}{2})\cdot(1,-1)}{\frac{3}{2}\cdot\sqrt{2}}=\frac{1}{\sqrt{2}}$$

題組13：函數圖形於某一點上的切線

只要確認兩圖形在 \(P\) 點的切線斜率相同即可。

$$f(x)=\frac{1}{2}x^2 \Rightarrow f'(1)=1 $$

$$x^2+y^2-3y+\frac{1}{4}=0 \Rightarrow 2x+2yy’-3y’|_{P(1,\frac{1}{2})}=0 \Rightarrow y'(1)=1$$

題組14：兩曲線所圍區域的面積。

我們先將圖形繪製如下：

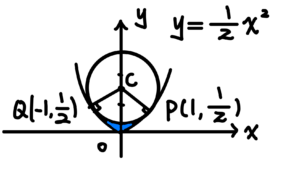
首先驗證 \(\angle{PCQ}=90^{\circ}\)：$$\overrightarrow{CP}\cdot\overrightarrow{CQ}=(1,-1)\cdot(-1,-1)=0$$

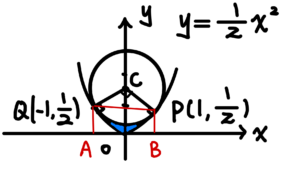
欲求之面積＝\(\Delta CPQ\) 面積 ＋ 長方形 \(ABPQ\) 的面積 \(-\) 扇形 \(CPQ\) 的面積 \(-\) 圖形 \(y=\frac{1}{2}x^2\) 與 \(x\) 軸所夾的面積
$$欲求之面積=\frac{1}{2}\cdot \sqrt{2}^2+2\cdot\frac{1}{2}-\pi\cdot\sqrt{2}^2\cdot\frac{1}{4}-\int_{-1}^1\frac{1}{2}x^2dx=\frac{5}{3}-\frac{\pi}{2}$$

15-17題組

可以先畫個簡圖看一下：

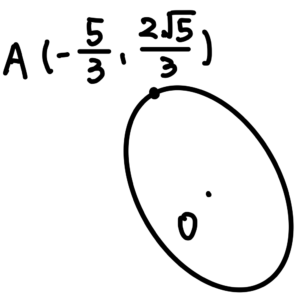
題組15：計算橢圓的長軸長

$$\begin{aligned}
長軸長 &= 2\cdot\overline{OA} \\
&= 2\cdot\sqrt{(-\frac{5}{3})^2+(\frac{2\sqrt{5}}{3})^2}\\
&= 2\cdot\frac{1}{3}\sqrt{25+20}=2\sqrt{5} \end{aligned}$$

題組16：計算橢圓短軸所在的直線方程式與短軸長

先算出直線 \(OA\) 的斜率，
$$m_{OA}=\frac{0-\frac{2\sqrt{5}}{3}}{0-(-\frac{5}{3})}=-\frac{2}{\sqrt{5}}$$ 因此

再利用兩直線垂直則其斜率相乘為 \(-1\) 求出短軸所在直線方程式 \(L’\) 的斜率。

$$m_L’=\frac{\sqrt{5}}{2}$$

因此 $$L’:\sqrt{5}x-2y=0$$

接下來計算短軸長：我們可以先算出直線 \(L’\) 與橢圓的交點。
利用代入消去法，將 \(y=\frac{\sqrt{5}}{2}x\) 代入橢圓方程式 \(40x^2+4\sqrt{5}xy+4y^2=180\)
$$40x^2+4\sqrt{5}x\cdot\frac{\sqrt{5}}{2}x+41\cdot(\frac{\sqrt{5}}{2}x)^2=180$$
整理式子可得 $$x^2=\frac{16}{9}$$因此 $$x=\pm\frac{4}{3}$$ \(B\) 點坐標為 \(B(\frac{4}{3},\frac{2}{3}\sqrt{5})\)

$$短軸長 = 2\times \overline{OB}=2\sqrt{(\frac{4}{3})^2+(\frac{2}{3}\sqrt{5})^2}=4$$

題組17：橢圓旋轉求其上一點

先畫出旋轉後的橢圓簡圖：

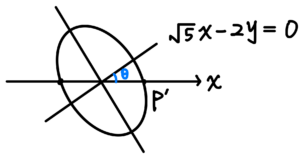
由圖可知，\(tan\theta=\frac{\sqrt{5}}{2}\)。設\(P'(x’,0)\)並代入原方程式可得 $$40x’^2=180 \Rightarrow x’=\frac{3}{\sqrt{2}}$$

設 \(P(x,y)\)，則
$$\left[\begin{array}{c}
x \\
y
\end{array}\right] =
\left[\begin{array}{cc}
cos\theta & sin\theta \\
-sin\theta & cos\theta
\end{array}\right]\cdot
\left[\begin{array}{cc}
\frac{3}{\sqrt{2}}\\
0
\end{array}\right] =
\left[\begin{array}{cc}
\frac{2}{3} & \frac{\sqrt{5}}{3} \\
– \frac{\sqrt{5}}{3} & \frac{2}{3}
\end{array}\right]\cdot
\left[\begin{array}{cc}
\frac{3}{\sqrt{2}}\\
0
\end{array}\right] =
\left[\begin{array}{cc}
\sqrt{2}\\
-\frac{\sqrt{10}}{2}
\end{array}\right]
$$

歷屆試題解析

作者介紹