前言
這個頁面整合高中數學免費資源,方便學生自學使用。在此之前,我已經編寫了第一冊及第二冊的部份,且以google搜尋關鍵字:高中數學第1冊、高中數學第2冊,皆能在第一頁找到這兩篇文章。
網路上有很多資源,可作為學習輔助使用。以下提供學習流程給學習者參考:
步驟1:上課時認真聽講,確實理解。
有些內容在課堂上聽不懂怎麼辦?此時可使用此頁面整理的資源加強並且釐清觀念。也可以參考均一教育平台高中數學課程頁面。
步驟2:完成單元練習。
課本或是參考書在每個單元之後,都會放一些練習題,一定要自己想過並且實際演練。不會做,可連到FB:高中數學討論區,將題目拍照後上傳。這個社團人數有12.8萬成員,有不少老師在裡面,通常提出的問題很快就會有人回應。以下建議問問題的方式提供參考:
問數學問題的注意事項:
- 明確的問題陳述:確保你清楚明確地陳述你的數學問題。描述問題的具體部分,包括你不理解的概念、方程式或步驟。
- 如果可能的話,提供相關的背景資訊,例如問題的來源、你的學習進度、先前的嘗試,以及你對問題的理解。這將有助於回答者更好地理解你的情況。
- 自己嘗試過:在尋求協助之前,試著自己解決問題。這不僅有助於提高你的數學能力,還可以幫助你更好地理解問題。
- 具體的問題:避免泛泛而談或過於模糊的問題。盡量提出具體、明確的問題,這樣回答者才能更容易理解你的需求並提供相應的協助。
- 尊重時間:如果你正尋求他人的幫助,請尊重他們的時間。確保你的問題準備充分,以便可以迅速得到解答,而不是要求他們從頭教授整個數學概念。
- 學習過程:不僅僅關注答案,也關注解決問題的過程。這將有助於你更好地理解和記住數學概念。
- 詢問多個資源:如果你在一個地方找不到滿意的答案,嘗試在不同的資源、網站或論壇尋找幫助。不同的角度和解釋方式可能有助於你更好地理解問題。
- 感謝和回饋:當你得到幫助時,不要忘記感謝回答者,並在有需要時提供回饋。這可以建立良好的學習社區和互惠關係。
總之,清晰的問題陳述、提供相關背景資訊、自己嘗試、尊重時間和學習過程都是尋求數學協助時應注意的要點,這樣你將更容易獲得有價值的幫助。
步驟3:測驗
測驗的部份,建議使用完整的考卷計時測驗,線上測驗的效果我覺得不好。
這份教材會持續編寫擴充,若你想獲得這份教材的更新通知,可於文章下方訂閱「高中數學數位學習電子報」。
若想接收關於高中數學線上教學的資訊,可加入以下line@官方帳號
- 高一、高二學生:高中數學線上教學
- 高三學生:高中數學學測指考教學
適合「自然組」或「商管學院」的學生
單元01 弧度量
弧度量的定義
網路免費資源:
習慣上,「角」的測量單位為「度」,相信同學們也用得很習慣了。在此我提出幾個問題作為我們這一節的學習目標:
1. 當我們寫30^{\circ}與30 所代表的意思是否相同?
我時常看到初學的學生會自動將「度」省略,這是常見的錯誤。一個粗淺的判斷,如果這兩者相同,那為何還要介紹「度」這個符號呢?數學家用字是很精準的,不可能如此累贅。因此,我們可以初步判斷,30^{\circ}與30是不一樣的。
2. 30^{\circ}是實數嗎?
如果是的話,那麼30^{\circ}應該畫在數線的什麼位置呢?它算是有理數還是無理數呢?
類比一下,我們知道 30 是一個實數,但如果寫成「30公分」,我們似乎不會說「30公分」是一個實數。也就是說,前面的 30 表示實數,後面的「公分」是單位,並且我們知道這是用來測量「長度」的單位。
同樣道理,「30^{\circ}」是一個測量「角度」的量,我們不會說「30^{\circ}」是一個實數。
3. 如何描述清楚「角度」與「數字」的函數關係?並且畫出其函數圖形?
這便是我們接下來學習的重點。因為三角函數是定義在「角度」上的函數,我們要將其畫在坐標平面,則必須將角度畫在「x」軸上,但是角度不是實數要怎麼畫上去呢?
這便是這一節的目的,將「角度」與「實數」做對應,讓我們可以將角度畫在「x」軸上。
這個與角度對應的實數就是這一節要介紹的「弳」(又稱「弧度」)。
4. 如何定義「弳」?
首先我們來看一下半徑為 r 的圓,看看角度與長度要如何對應:
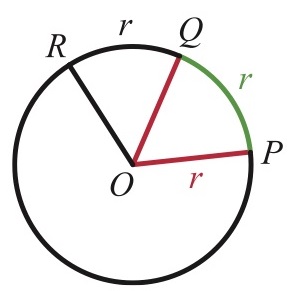
我們知道,圓一圈是「360^{\circ}」,圓周長是「2\pi\times r」
對於圓心角為 \theta^{\circ} 的弧長為
2\pi\times r \times \frac{\theta^{\circ}}{360^{\circ}}= 2\pi\times\frac{\theta^{\circ}}{360^{\circ}}\times r
由於我們關注的是「角度」,不會受到半徑大小的影響。因此\theta^{\circ} 會對應到實數2\pi\times\frac{\theta^{\circ}}{360^{\circ}}
我們便以實數 2\pi\times\frac{\theta^{\circ}}{360^{\circ}}來表示角度 \theta^{\circ}
也就是說1^{\circ}=\frac{\pi}{180}(弳)
我們可以按按計算機,看看1弳大約是幾度:1弳=(\frac{180}{\pi})^{\circ}\approx 57.2958^{\circ}
將「度」與「弳」兩種單位快速換算是基本能力,初學應多加練習。
弧長與扇形面積
網路免費資源:
接下來我們來談談,如何計算扇形的弧長與面積。這部份在國中三年級的課程已有介紹,我們在高中階段試著用「弳」這個單位寫看看。如下圖所示,


用「弳」來表示扇形的「弧長」及「面積」,其形式看起來更為簡潔。近年大考命題會測試學生是否能夠清楚區分這兩種單位的差別。
以上觀念建立好了,接下來就可以好好演練題目了。這一節的題目有不少變化也不乏難題,請先將課本題目做熟後,再做其他延伸。
以弳為單位的三角比
接下來來談談三角比。這裡不是新的內容,只是換成不同的角度單位來表示而已。學生必須練習到能夠熟練地將「弳」自然地想到對應的位置,這一節大致如此。
學生在學習這一段內容時必須辨別「弳度」與「度」的三角比的差異,例如以下這道題目,有助於釐清觀念:
下列哪些不等式成立?
(1) sin{\pi}>sin{(\pi)^{\circ}}
(2) cos{\pi}>cos{\pi}^{\circ}
(3) cos{\pi}^{\circ}>sin{\pi}^{\circ}
(4) tan{\pi}>tan{\pi}^{\circ}
(5) sin{\frac{\sqrt{3}}{2}}<\frac{\sqrt{3}}{2}
選項(1):首先,我們要思考 \pi 與 \pi^{\circ} 的差別是什麼呢?
\pi 對應到 180^{\circ})、(\pi^{\circ}\approx 3.14^{\circ})
因此 sin{\pi}=0<sin{\pi^{\circ}}
選項(2):cos{\pi}=-1<0<cos{\pi^{\circ}}
選項(3):因為 0^{\circ}<\pi^{\circ}<45^{\circ},所以
cos{\pi^{\circ}}>sin{\pi^{\circ}}
選項(4):tan{\pi}=0<tan{\pi^{\circ}}
選項(5):因為 \frac{\sqrt{3}}{2}=sin{\frac{\pi}{3}}\approx sin1.047,且sin (\frac{\sqrt{3}}{2})\approx sin0.866。又因為 y=sinx 在第一象限為遞增函數,所以 sin{\frac{\sqrt{3}}{2}}<sin{\frac{\pi}{3}}=\frac{\sqrt{3}}{2}
單元02 三角函數的圖形
在各三角比都有定義的情形下,給定一個廣義角 x,sinx、cosx、tanx 的值都隨之唯一確定,因此都可以視為 (x) 的函數。依序稱為正弦函數、餘弦函數與正切函數。
要留意不可忽略這些函數的名稱,因為曾經就有大考題問某個角度的正切值是多少?
如果不知道正切值就是 tanx,那麼這一題即使會寫也答不上來。
繪製三角函數圖形的要點
- 要點1:必須熟悉象限角的三角函數值
- 要點2:觀察圖形的「定義域」、「值域」、「週期」、「振幅」、「對稱性」
- 要點3:圖形的平移與伸縮
網路資源
單元03 三角的和差角公式
這個單元有四個重點
重點1:什麼是「正弦」與「餘弦」函數的和差角公式,如何推導?
\begin{aligned} sin(\alpha\pm\beta) &= sin\alpha cos\beta\pm cos\alpha sin\beta \\ cos(\alpha\pm\beta) &= cos\alpha cos\beta\mp sin\alpha sin\beta \end{aligned}
網路資源
重點2:如何推導出「正切」函數的和差角公式?
網路資源
重點3:如何推導出「正弦」、「餘弦」、「正切」函數的二倍角公式?
以及「正餘弦」的半角、三倍角公式?
這裡的公式看似很多,其實本質就是「餘弦定理」以及「三角函數的轉換關係」,推導過程對於初學者是非常好的練習,切勿只是將公式背下來套用在題目上,而是要真正了解公式的來龍去脈,學習到公式的內涵本質而非只是表象的形式。
網路資源
重點4:如何使用以上公式解決問題?
公式的形式及推導熟悉後,可以藉由適量地練習一些題目強化觀念並且熟記公式。首先要先將課本的範例、習題做過一遍,如果心有餘力,可再另外採購題本提升自己的解題技巧。
單元04 正餘弦的疊合
這個單元主要介紹如何將正弦函數 y=sinx 及餘弦函數 y=cosx 複合成一個函數。我們處理的一般形式為 y=asinx+bcosx
學習要點1:如何將 y=asinx+bcosx 複合成以下形式
y=asinx+bcosx=\sqrt{a^2+b^2}sin(x+\theta)
其中 \theta 滿足 cos\theta=\frac{a}{\sqrt{a^2+b^2}}, sin\theta=\frac{b}{\sqrt{a^2+b^2}}
學習要點2:探討 y=asinx+bcosx 極值及極值發生的位置(角度)
我們知道,
\begin{aligned} 當 &x+\theta=2k\pi+\frac{\pi}{2} 時,y 有最大值 \sqrt{a^2+b^2} \\ 當 &x+\theta=2k\pi+\frac{3\pi}{2} 時,y 有最小值-\sqrt{a^2+b^2} \end{aligned}
我們不妨先考慮 k=0 的情況:當 sinx=sin(\frac{\pi}{2}-\theta) 時,其函數值最大。
另一方面,當 sinx=sin(\frac{3\pi}{2}-\theta) 時,其函數值最小。
其中 sinx=sin(\frac{\pi}{2}-\theta)=cos\theta=\frac{a}{\sqrt{a^2+b^2}}
sinx=sin(\frac{3\pi}{2}-\theta)=-cos\theta=-\frac{a}{\sqrt{a^2+b^2}}
單元05 指數函數
課程內容
- 何謂指數函數?
- 如何描繪指數函數的圖形?
- 指數函數的圖形有何特徵?
- 指數函數有哪些應用?
指數方程式、指數不等式、指數函數在金融的應用 - 課外補充:如何證明e是無理數?
- 作業討論
單元06 指數與對數律
課程內容
- 什麼是對數,如何定義?
- 對數律與換底公式
公式推導與應用:換底公式 - 常用對數與科學記號
如何判斷一個很大的數是幾位數? - 作業討論
單元07 對數函數
課程內容
- 什麼是對數函數?
- 如何描繪對數函數的圖形?
- 對數函數的圖形有何特徵?
- 對數函數有哪些應用呢?
- 作業討論
單元08 平面向量
課程內容
- 向量的表示法:「幾何表示法」與「座標表示法」
- 向量的加法與減法:坐標表示及其性質。
- 向量的係數積:定義及基本性質
- 向量的線性組合
- 向量的分點公式
- 作業討論
單元09 平面向量的運算
課程內容
- 什麼是向量的內積?為什麼要這樣定義呢?
- 何謂向量的正射影?
- 什麼是柯西不等式
課外補充:一般柯西不等式的證明 - 二階行列式的幾何意義為何?
單元10 二元一次聯立方程式
課程內容
- 什麼是加減消去法?
- 什麼是克拉瑪公式?
- 何謂二元一次聯立方程式的幾何意義?
- 二階行列式有哪些性質?
- 二元一次聯立方程式的向量觀點

