已知三角形 \(\Delta ABC\) 中，\(\angle{A}、\angle{B}、\angle{C}\) 的對邊長分別為 \(a\)、\(b\)、\(c\)，則 $$\Delta ABC的面積= \sqrt{s(s-a)(s-b)(s-c)}$$ 其中 \(s=\frac{a+b+c}{2}\)。

在談這個公式的由來之前，我曾經遇過學生，面對三角形的三邊長為無理數時，仍然使用這個公式求面積，結果處理雙重根式的過程中，遇到不小的麻煩。

例如：如果此三角形的三邊長為 \(\sqrt{3}、\sqrt{5}、\sqrt{7}\) 時，如何求其面積呢？

所以，理論上，已知三角形的三邊長可以代入海龍公式沒錯，但實際使用上，我們還是要變通一下。
通常，我會這樣處理：
首先，先利用餘弦定理求出其中一個角度(例如\(\angle{A}\))的餘弦值 $$cosA=\frac{\sqrt{3}^2+\sqrt{5}^2-\sqrt{7}^2}{2\times\sqrt{3}\times\sqrt{5}}=\frac{1}{2\times\sqrt{3}\times\sqrt{5}}$$ 接著換為正弦值 $$sinA=\frac{\sqrt{59}}{2\sqrt{15}}$$最後再計算面積 $$\Delta ABC的面積 = \frac{1}{2}\sqrt{3}\times\sqrt{5}\times sinA = \frac{1}{2}\sqrt{3}\times\sqrt{5}\times \frac{\sqrt{59}}{2\sqrt{15}} = \frac{\sqrt{59}}{4} $$ 這樣做會比直接代海龍公式簡單得多。

接著我們來探討，這個公式是怎麼出現的？不妨先猜個答案，接著再設法證明我們的猜測是正確的！
證明的部份，我會先幫同學們複習教科書的證法，接著再循著歷史的軌跡看看以前數學家是如何證明的！

猜測海龍公式

設 \(\Delta ABC\) 的面積為 \(S(a,b,c)\)，也就是一個與 \(a,b,c\) 有關的函數。那麼這樣的函數有什麼特性呢？

第一、對稱性：$$S(a,b,c)=S(a,c,b)=S(b,a,c)=S(b,c,a)=S(c,a,b)=S(c,a,b)=S(c,b,a)$$

換句話說，三角形的面積與三邊長所在的位置無關，這很顯然。

第二、如果 \(a+b=c\) 或 \(b+c=a\) 或 \(c+a=b\)，那麼這三邊長無法構成三角形，只能是一條線段，因此 $$S(a,b,c)=0$$

也就是說，\(S(a,b,c)\) 中有因式 \(b+c-a、a+c-b、a+b-c\)

然而我們要再考慮，三角形的單位是長度的平方，不可能是三段長度相乘，那麼我們就再補一段，使其變為長度的四次方再開根號。可是應該補那一段才可以維持對稱性呢？

\(a+b+c\) 是不錯的選擇，不妨試試！

設 $$S(a,b,c)=\sqrt{K(a+b+c)(b+c-a)(a+c-b)(a+b-c)}$$ 我們要再來決定常數\(K\)，

考慮特例：如果這是個邊長為\(1\)的正三角形，則 $$\frac{\sqrt{3}}{4}=S(1,1,1)=\sqrt{K\cdot 3}$$

等式兩邊平方可得 \(K=\frac{1}{16}\)

接著將此公式整理一下：
$$\begin{aligned}
S(a,b,c) &= \sqrt{\frac{a+b+c}{2}\cdot\frac{b+c-a}{2}\cdot\frac{a+c-b}{2}\cdot\frac{a+b-c}{2}} \\
&= \sqrt{s(s-a)(s-b)(s-c)}
\end{aligned}$$

可以代幾組數字到此公式檢驗，加強信心。
雖然這樣做不是非常嚴謹，卻是數學研究者時常在做的事，學習猜測答案也是一個很重要的能力。

接著我們來推導這個公式囉！

海龍公式的證明1：初等方法，國中生也可以懂 – 代數觀點

這個證明只須用到畢氏定理即可，為了不讓這篇文章太過繁瑣，我只證明銳角三角形的部份。同樣的方法可以用在鈍角與直角三角形上面，就留給讀者自行練習了。

第一步：先過\(A\)點作高\(\overline{AH}\)，並且假設 \(\overline{CH}=x\)，則\(\overline{BH}=a-x\)

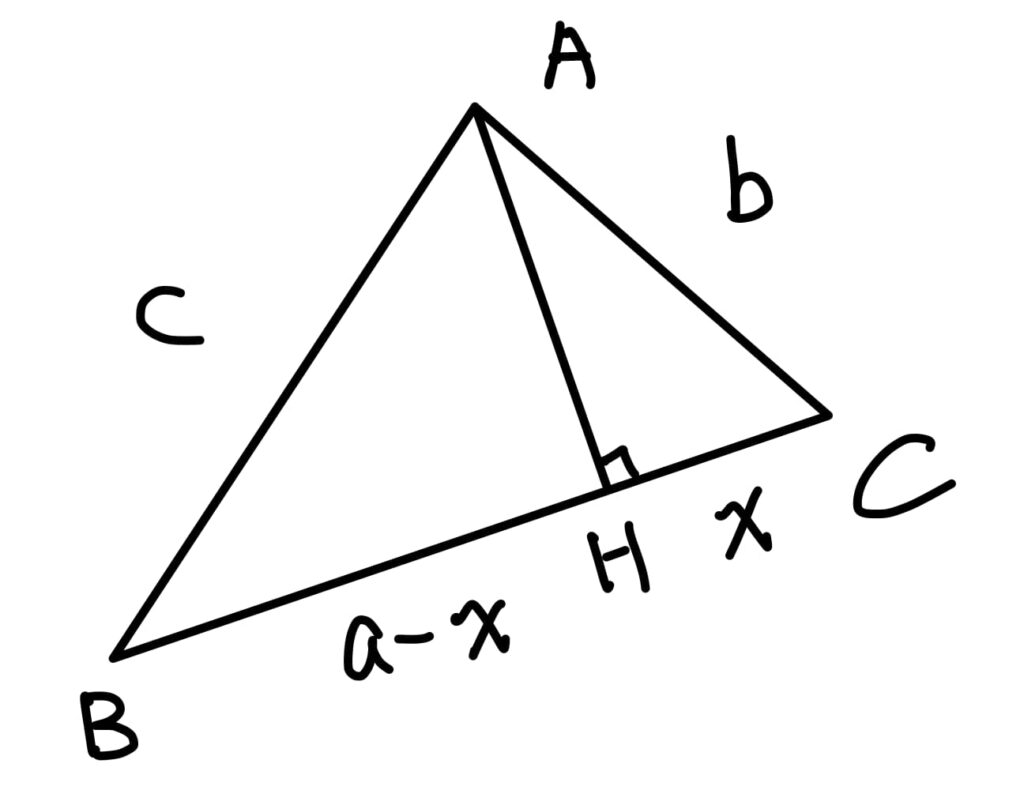
分別在 \(\Delta ABH\) 及 \(\Delta ACH\) 使用畢氏定理：
$$\overline{AH}^2=c^2-(a-x)^2 = b^2 – x^2$$ 移項整理可得 $$x=\frac{a^2+b^2-c^2}{2a}$$ 已經有海龍公式的雛形了。
第二步：我們以\(\overline{BC}\)為底，求高\(\overline{AH}\)：
$$\begin{aligned}
\overline{AH}^2=b^2-x^2 &= (b+x)(b-x) \\
&= (b+\frac{a^2+b^2-c^2}{2a})\cdot(b-\frac{a^2+b^2-c^2}{2a}) \\
&=(\frac{a^2+2ab+b^2-c^2}{2a})\cdot(\frac{c^2-a^2+2ab-b^2}{2a})\\
&=\frac{(a+b)^2-c^2}{2a}\times\frac{c^2-(a-b)^2}{2a}\\
&=\frac{(a+b+c)(a+b-c)}{2a}\times\frac{(c+a-b)(c-a+b)}{2a}\\
&=\frac{2s(2s-2c)(2s-2b)(2s-2a)}{4a^2}
\end{aligned}$$

因此，
$$\begin{aligned}
\Delta ABC 的面積 &= \frac{1}{2}\cdot a \cdot \overline{AH} \\
&= \frac{1}{2}\cdot a \cdot \frac{\sqrt{16s(s-a)(s-b)(s-c)}}{2a}\\
&= \sqrt{s(s-a)(s-b)(s-c)}
\end{aligned}$$

想要真正學好數學，必須熟悉符號的操作，這個推導方式不會太難，可作為入門高中數學一個很好的訓練。

海龍公式的證明2：使用三角函數恆等式 – 代數觀點

接下來介紹的這個方法，是高中數學教科書介紹的方法，其過程也是較著重代數運算。與方法1不同的是，這個做法較具有一般性，不依賴三角形的種類(銳角、鈍角、直角)，其寫法都一樣。過程中須要用到三角恆等式的「平方關係」以及「餘弦定理」，我們很快來複習一下：
$$\begin{aligned}
\Delta ABC 的面積 &= \frac{1}{2}bcsinA \\
&= \frac{1}{2}bc\sqrt{1-cos^2A} \\
&= \frac{1}{2}bc\sqrt{(1+cosA)\times (1-cosA)}\\
&= \frac{1}{2}bc\sqrt{(1+\frac{b^2+c^2-a^2}{2bc})\times(1-\frac{b^2+c^2-a^2}{2bc})} \\
&= \frac{1}{2}bc\sqrt{\frac{b^2+2bc+c^2-a^2}{2bc}\times \frac{a^2-b^2+2bc-c^2}{2bc}}\\
&= \frac{1}{2}bc\sqrt{\frac{(b+c)^2-a^2}{2bc}\times\frac{a^2-(b-c)^2}{2bc}}\\
&= \frac{1}{2}bc\sqrt{\frac{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}{4b^2c^2}}\\
&= \sqrt{\frac{2s(2s-2a)(2s-2b)(2s-2c)}{16}}\\
&= \sqrt{s(s-a)(s-b)(s-c)}
\end{aligned}$$

這種代數證明方式看似繁瑣，但只要多練習幾次，通常很容易就上手了。

接下來才是我們這篇文章主要想談的部份：當初海龍是如何推導出海龍公式的呢？
海龍(Heron of Alexandria) 大約是西元一世紀的數學家，當時是正餘弦的觀念還不成熟，而且代數還不發達的時代。我們的教科書為了讓內容可以被學生們普遍接受，大多會選擇較簡單且方便的數學工具說明，而不一定是從符合歷史觀點的角度出發。我第一次看到海龍的證明時，實在讚嘆古人真是太聰明了！

海龍公式的證明3：海龍的原始想法，利用相似三角形 – 幾何觀點

回想一下海龍公式中，已知\(s\)是三角形的半周長，然而\(s-a\)、\(s-b\)、\(s-c\)在圖形上是代表什麼意思呢？
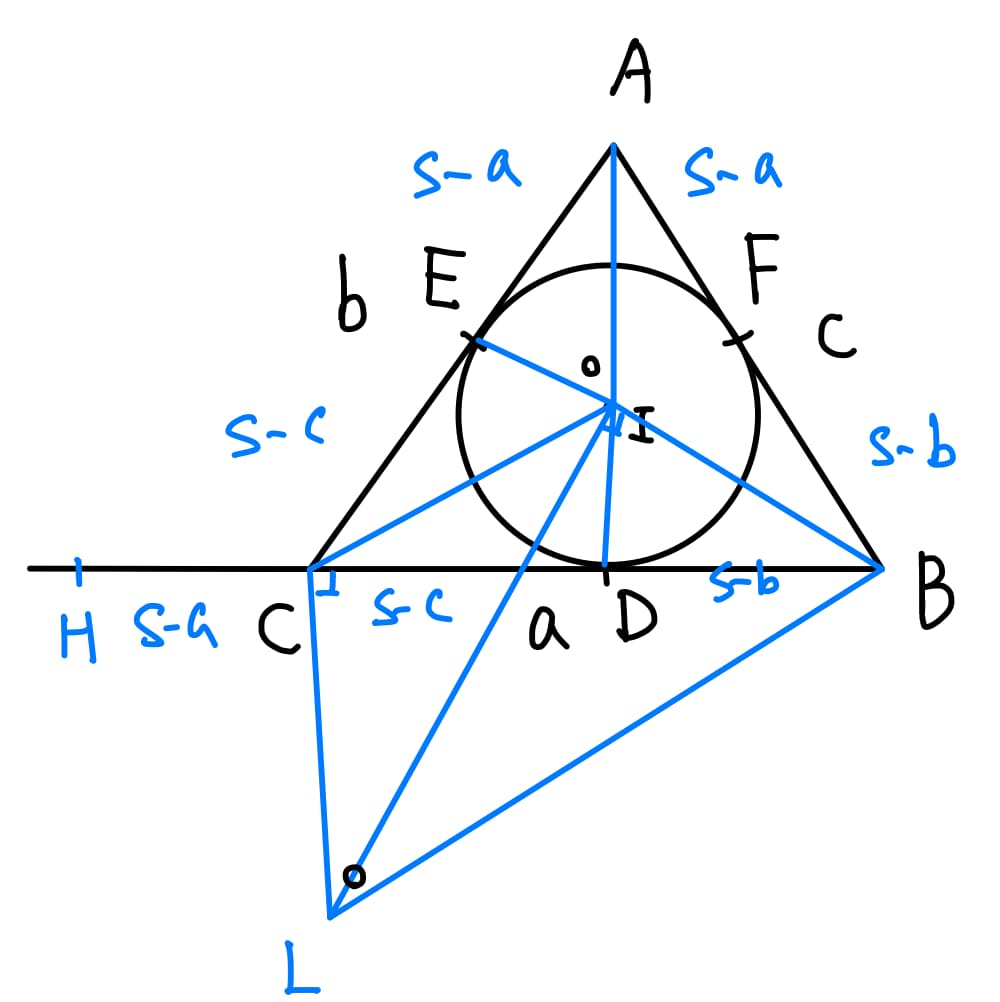
答案是，與三角形的內切圓有關，如下圖所示：

設此內切圓與三角形三邊的切點分別為\(D\)、\(E\)、\(F\)，並且可知
$$\overline{AE}=\overline{AF}=s-a、\overline{BD}=\overline{BF}=s-b、\overline{CE}=\overline{CD}=s-c$$

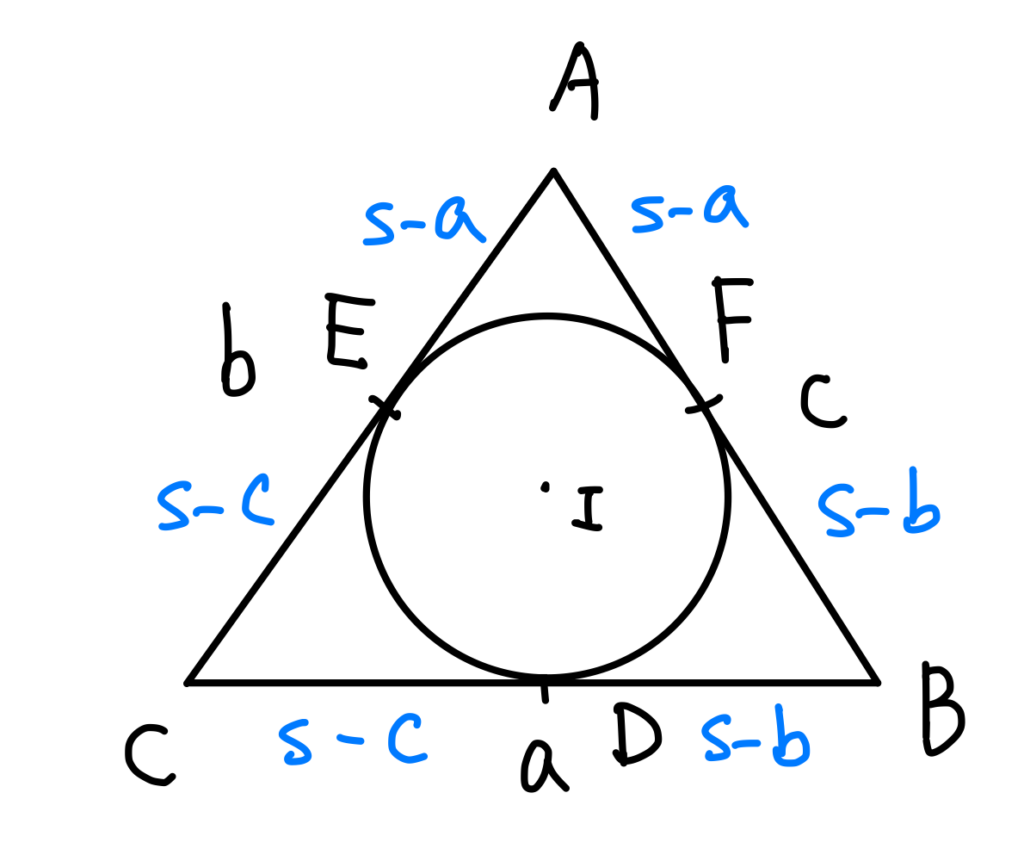
另外，我們已知一個簡單的事實：三角形的面積＝半周長×內切圓半徑。因此，目標是去證明
$$rs=\sqrt{s(s-a)(s-b)(s-c)}$$ 其中\(r\)是內切圓半徑。

接著將上式平方後，等式兩邊同時除以\(s(s-a)\)可得：
$$\frac{s^2}{s(s-a)}=\frac{(s-b)(s-c)}{r^2}$$
寫到這裡，我們大概猜得到海龍想做什麼了，他想找出兩個相似三角形！接下來就來欣賞海龍的巧思吧。
首儿，延長\(BC\)至\(BH\)使得\(\overline{CH}=s-a\)，此時\(\overline{BH}=s\)。

接下來將圓心\(I\)連接\(\Delta ABC\)的三頂點：

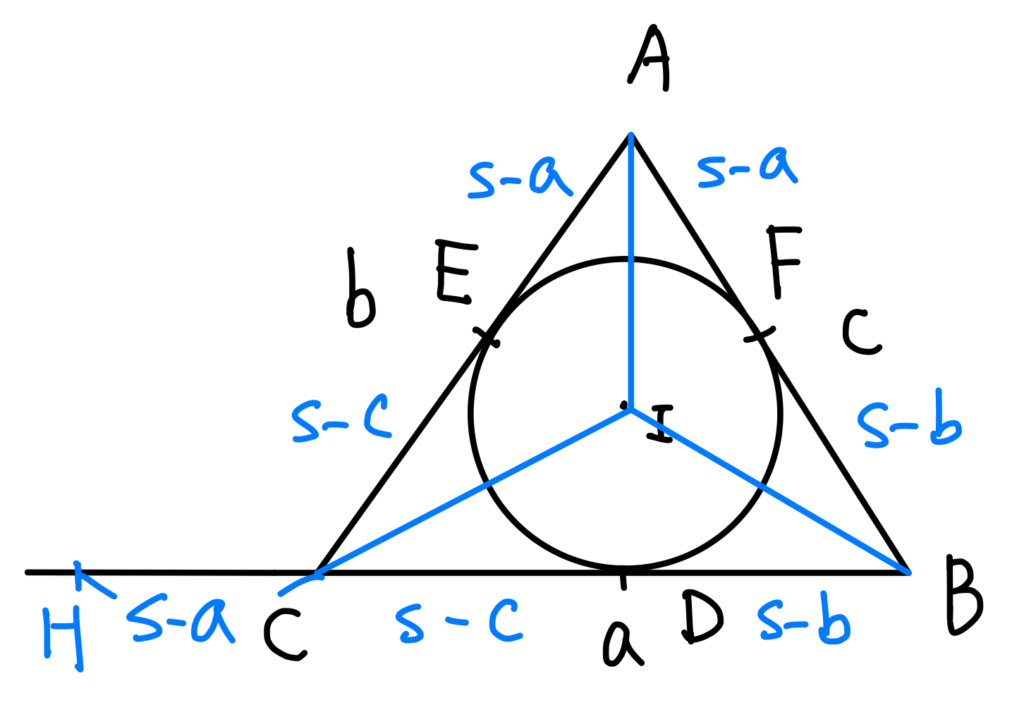
重點來了，這真的非常不容易想到，就是過\(I\)、\(C\)兩點分別作\(BI\)及\(BC\)之垂線且兩垂線相交於\(L\)，如下圖所示：

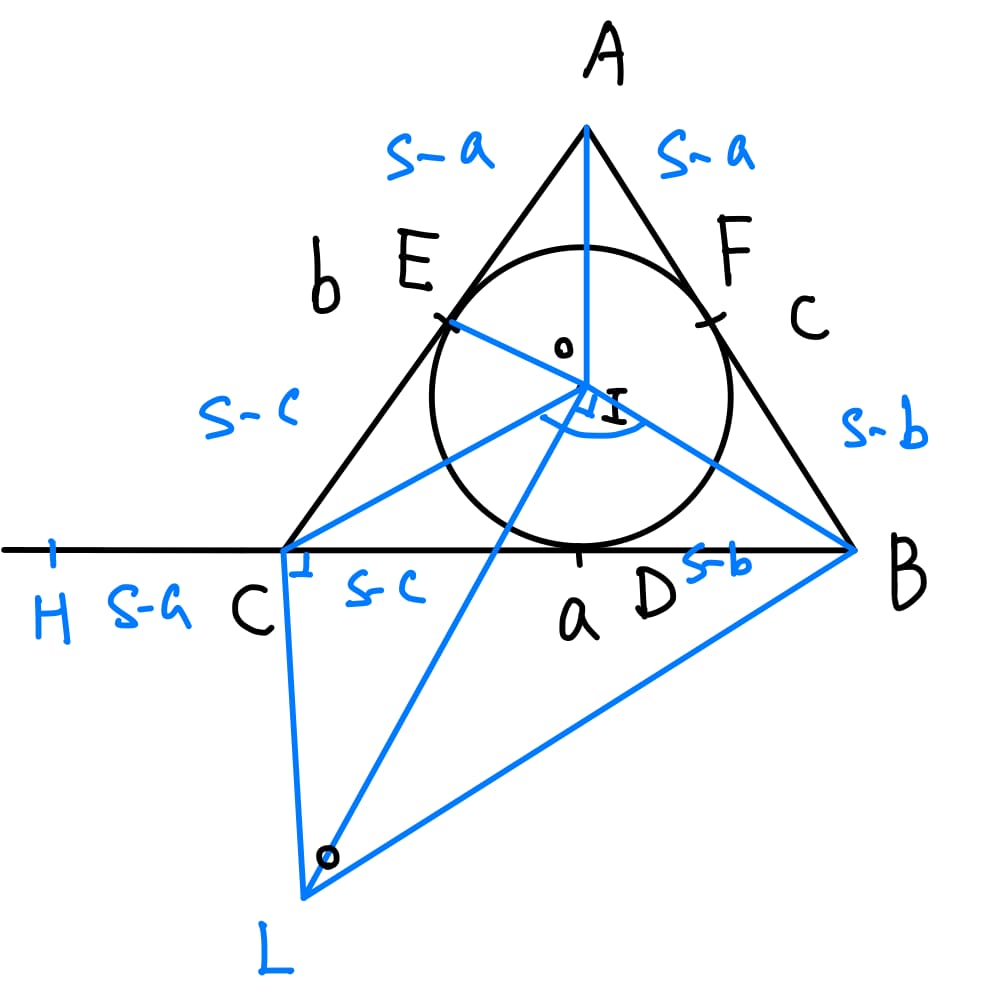
為了避免讀者迷失在論證當中，先說說接下來的目標是要去證明 \(\Delta AEI \sim \Delta BCL\)，這兩個皆為直角三角形，我們只須再說明還有一組角度相同即可。

首先，因為\(\angle{BIL}=\angle{BCL}=90^{\circ}\)，所以\(B,I,C,L\)四點共圓，此圓就是以\(\overline{BL}\)的中點為圓心，\(\frac{1}{2}\times\overline{BL}\)為半徑的圓。
因此\(\angle{BIC}+\angle{BLC}=180^{\circ}\)。接著我們將\(ID\)連起來。

$$\begin{aligned}
\angle{BIC} &= \angle{BID}+\angle{CID} \\
&= (90^{\circ}-\frac{1}{2}\angle{ABC})+(90^{\circ}-\frac{1}{2}\angle{ACB}) \\
&=180^{\circ}-\frac{1}{2}(\angle{ABC}+\angle{ACB}) \\
&=180^{\circ}-\frac{1}{2}(180^{\circ}-\angle{BAC}) \\
&=90^{\circ}+\frac{1}{2}\angle{BAC}
\end{aligned}$$

因為圓內接四邊形的對角互補，因此
$$\begin{aligned}
\angle{BLC}&=180^{\circ}-\angle{BIC} \\
&=180^{\circ}-(90^{\circ}+\frac{1}{2}\angle{BAC}) \\
&=90^{\circ}-\frac{1}{2}\angle{BAC}\\
&=\angle{AIE}
\end{aligned}$$

故 $$\Delta AEI \sim \Delta BCL$$

設\(\overline{IL}\)與\(\overline{BC}\)交於點\(J\)。

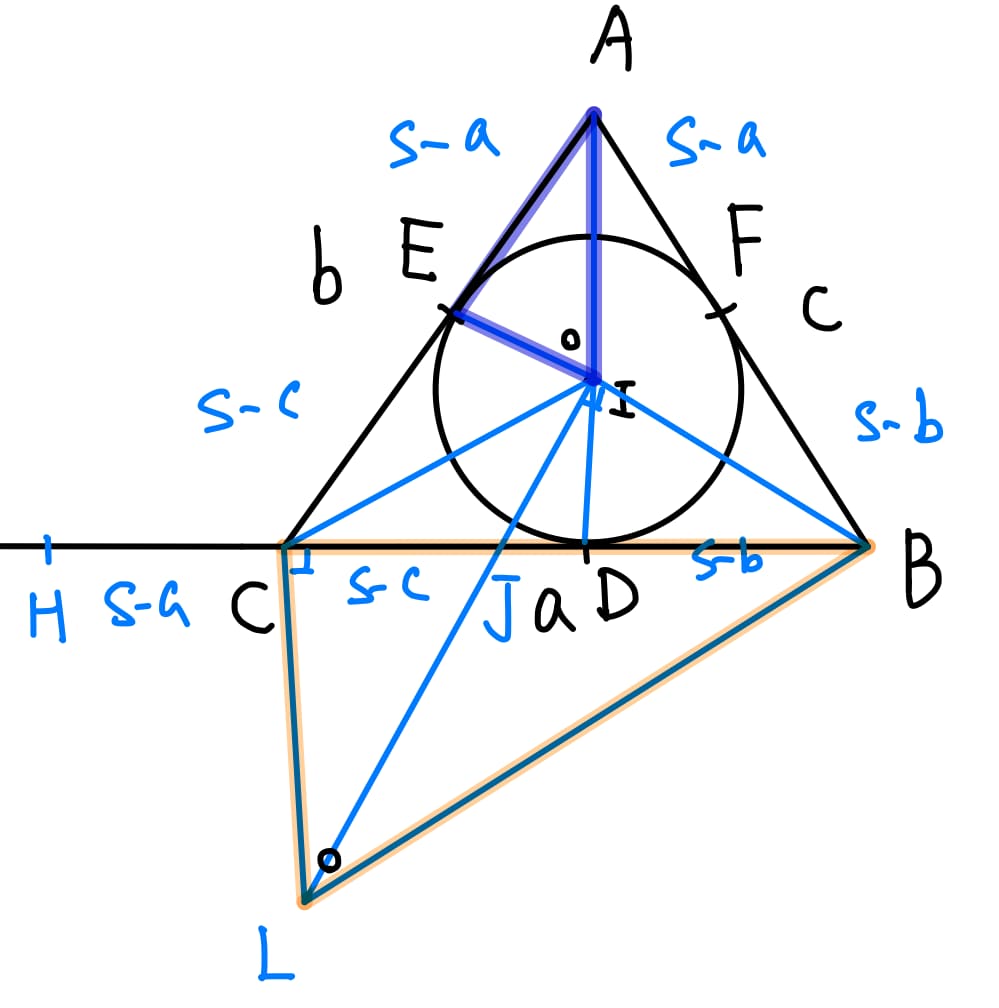
因為 \(\Delta AEI \sim \Delta BCL\) 且 \(\overline{IE}=\overline{ID}\)，所以
$$\frac{\overline{BC}}{\overline{AE}}=\frac{\overline{CL}}{\overline{IE}} = \frac{\overline{CL}}{\overline{ID}}$$
而且 \(\Delta{IDJ}\sim\Delta{LCJ}\)，故 $$\frac{\overline{CL}}{\overline{ID}}=\frac{\overline{CJ}}{\overline{DJ}}$$
結合上式可得 $$\frac{\overline{BC}}{\overline{AE}}=\frac{\overline{CJ}}{\overline{DJ}}$$

又 \(\overline{CH}=\overline{AE}\)，故
$$\begin{aligned}
\frac{\overline{BH}}{\overline{CH}} = \frac{\overline{BC}+\overline{CH}}{\overline{CH}}=\frac{\overline{BC}}{\overline{CH}}+1=\frac{\overline{BC}}{\overline{AE}}+1=\frac{\overline{CJ}}{\overline{DJ}}+1=\frac{\overline{CD}}{\overline{DJ}}
\end{aligned}$$

故
$$\begin{aligned}
\frac{\overline{BH}^2}{\overline{BH}\cdot\overline{CH}}=\frac{\overline{BH}}{\overline{CH}}=\frac{\overline{CD}}{\overline{DJ}}=\frac{\overline{BD}\cdot\overline{CD}}{\overline{BD}\cdot\overline{DJ}}=\frac{\overline{BD}\cdot\overline{CD}}{\overline{ID}^2} (母子相似性質)
\end{aligned}$$

即 $$\overline{BH}^2\cdot\overline{ID}^2=\overline{BH}\cdot\overline{CH}\cdot\overline{BD}\cdot\overline{CD}$$

以符號表示如下：$$s^2\cdot r^2 = s\cdot (s-a) \cdot (s-b) \cdot (s-c)$$

因此 $$\Delta ABC 的面積 = sr = \sqrt{s(s-a)(s-b)(s-c)}$$ 得證。

這篇文章就先寫到這邊，提供給有興趣的讀者參考。

---