歡迎訂閱，高中數學數位學習電子報

試題與解答下載

前言

數學是一門深具挑戰性與美感的學科，它不僅僅是一系列數字和符號的組合，更是一種邏輯思考和問題解決的藝術。在這份考題分析中，我們將深入探討113年學測數A這份試卷，旨在啟發學生對數學的思考方式，培養學生的問題解決能力。

首先，我會依照課程目錄將此次考題分類，並且統計各冊佔比。接著我將一一剖析每個考題的背後邏輯，以及解決問題的可能途徑。這不僅有助於學生理解每個問題的本質，更有助於提升解題能力，使學生在未來面對各種數學挑戰時更加游刃有餘。

我們鼓勵你積極參與分析過程，思考不同的解題思維，並隨著逐題解釋一同深入了解每個問題的解決過程。這將有助於你建立堅實的數學基礎，同時培養你在數學領域中的創造性和靈活性。

祝你在本次分析中獲得豐富的收穫，並在數學的世界中不斷探索與成長。

試題比重分析

第一冊(30分)	第二冊(25分)	第三冊(25分)	第四冊(20分)
第1章 實數與指對數(10分)	第1章 數列與級數(5分)	第1章 三角函數(10分)	第1章 空間向量(5分)
1.1實數	1.1數列與數學歸納法 多選8-綜合	1.1三角函數的圖形	1.1空間概念
1.2絕對值	1.2級數	1.2三角的和角與差角公式 單選4、單選6	1.2空間向量的坐標表示法：單選2
1.3指數 單選1			1.3空間向量的內積
1.4常用對數 多選7			1.4外積、體積與行列式
第2章 直線與圓(5分)	第2章 數據分析(5分)	第2章 指數與對數函數	第2章 空間中的平面與直線(5分)
2.1直線方程式及其圖形	2.1一維數據分析	2.1指數函數	2.1平面方程式 題組18
2.2直線方程式的應用 選填17-二元一次不等式	2.2二維數據分析 多選9	2.2對數與對數律	2.2空間中的直線
2.3圓方程式		2.3對數函數
2.4圓與直線的關係
第3章 平面向量(15分)	第3章 排列組合與機率(15分)	第3章 平面向量(15分)	第3章 條件機率與貝氏定理
3.1多項式的運算與應用 選填14	3.1基本計數原理	3.1平面向量的運算 多選10	3.1條件機率與獨立事件
3.2多項式及其圖形 題組20	3.2排列	3.2平面向量的內積 選填16、題組19	3.2貝氏定理與主觀、客觀機率
3.3多項式不等式 單選3	3.3組合 單選5	3.3平面向量的應用
	3.4機率 多選11-綜合 選填15-期望值
	第4章 三角比		第4章 矩陣(10分)
	4.1直角三角形的三角比		4.1一次方程組 選填13
	4.2廣義的的三角比		4.2矩陣的運算
	4.3三角比的性質		4.3矩陣的應用 多選12

題型及試題內容分析

單選第1題：半衰期問題(易)

這一題很簡單，是標準的半衰期問題，設服用\(t\)小時後，體內殘留藥物為$$f(t)=f(0)\cdot(\frac{1}{2})^{\frac{t}{2}}$$
那麼用\(4\)個小時後，藥物剩下\((\frac{1}{2})^2=\frac{1}{4}\)劑量，答案選(2)。

單選第2題：空間向量(易)

我也是常考題了，可以將圖形座標化：以\(A\)點為原點，射線\(\overrightarrow{AB}\)為正向\(x\)軸方向，直線\(\overrightarrow{AE}\)為正向\(y\)軸方向，如下圖所示。

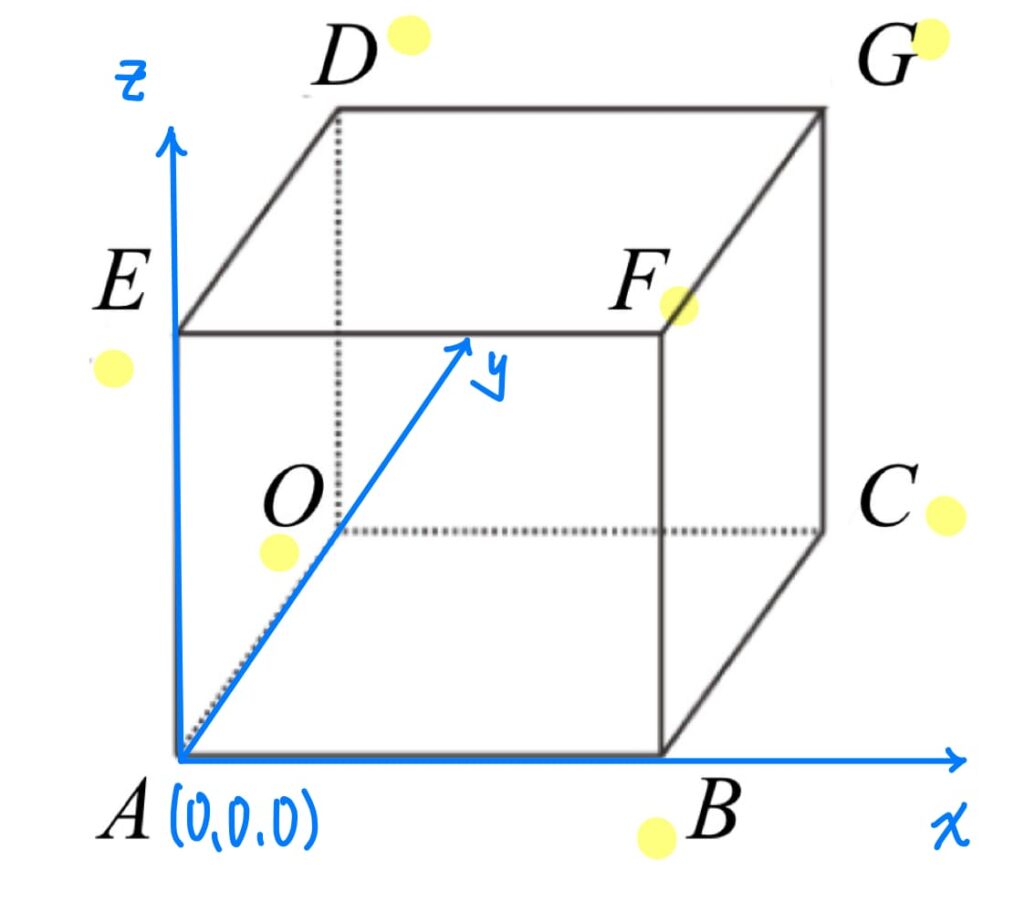
接著，不妨假設此正方體的邊長為\(1\)，並標上各頂點座標：

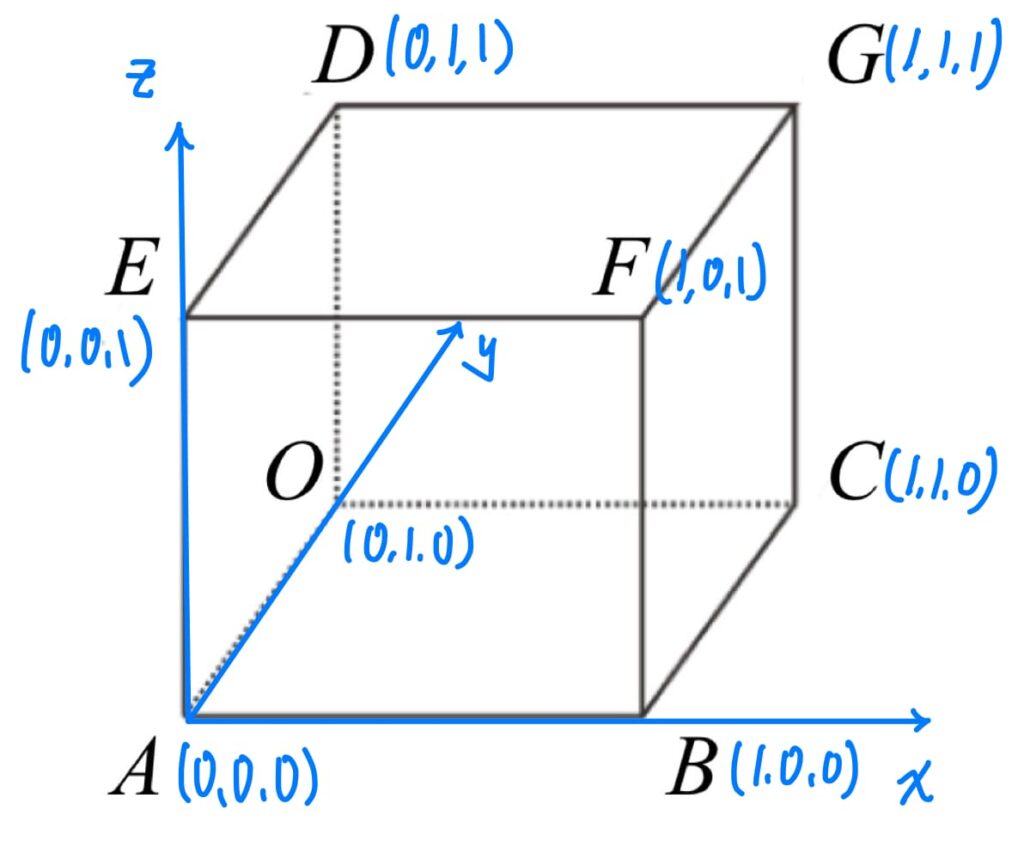
計算 $$\overrightarrow{AD}\times \overrightarrow{AG}=(0,1,1)\times (111) = (0,1,-1)$$
依序寫上各向量座標比較一下：

$$\begin{aligned}
(1) \overrightarrow{AE} &= (0,0,1) \\
(2) \overrightarrow{BE} &= (-1,0,1) \\
(3) \overrightarrow{CE} &= (-1,-1,1) \\
(4) \overrightarrow{DE} &= (0,-1,0) \\
(5) \overrightarrow{OE} &= (0,-1,1) \\
\end{aligned}$$

只有向量\( \overrightarrow{OE}\) 平行向量\( \overrightarrow{AD}\times \overrightarrow{AG}\)，因此答案選(5)

單選第3題：多項式不等式(中等難度)

依題意 $$設 \ f(x) = a (x+7)(x+7-a)(x+7-2a)$$

$$\begin{aligned}
f(0) > 0 & \Rightarrow a\cdot 7 \cdot (7-a) \cdot (7-2a) > 0 \\
& \Rightarrow a\cdot 7 \cdot (a-7) \cdot (2a-7) > 0 \\
& \Rightarrow a>7 \ \ or \ \ 0<a<\frac{7}{2}
\end{aligned}$$

因此，\(a=2\)是唯一可能，答案選(1)。

單選第4題：三角函數的和角公式(中偏難)

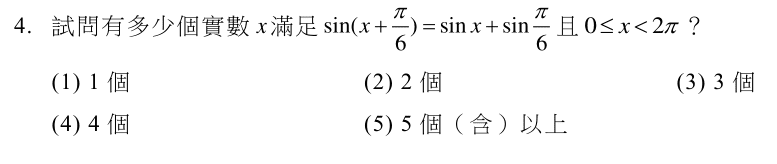
這一題第一步，可以先用正弦的和角公式拆開整理如下：

$$sinx\cdot \frac{\sqrt{3}}{2} + cosx \cdot \frac{1}{2} = sinx + \frac{1}{2} $$

移項整理，並且將等式全部乘以2，可將式子改寫為
$$(\sqrt{3}-2)sinx+cosx=1$$
接著將三角函數疊合，並且有理化分母，再整理可得
$$(\sqrt{6}-\sqrt{2})(\frac{\sqrt{2}-\sqrt{6}}{4}sinx+\frac{\sqrt{6}+\sqrt{2}}{4}cosx)=1 \tag{1}$$
其中，$$cos\frac{7}{12}\pi = \frac{\sqrt{2}-\sqrt{6}}{4}, \ sin\frac{7}{12}\pi=\frac{\sqrt{6}+\sqrt{2}}{4}$$
再回到第(1)式 $$(\sqrt{6}-\sqrt{2})(sinxcos\frac{7}{12}\pi +cosxsin\frac{7}{12}\pi)=1$$ 利用和角公式合併：
$$sin(x+\frac{7}{12}\pi)=\frac{1}{\sqrt{6}-\sqrt{2}}=\frac{\sqrt{6}+\sqrt{2}}{4}=sin\frac{5}{12}\pi$$
在限制 \(0\leq x < 2\pi\) 的情況下 $$x+\frac{7}{12}\pi = \frac{7}{12}\pi, 2\pi+\frac{5}{12}\pi $$
滿足原題意的 \(x=0, \ \frac{11}{6}\pi\)，因此答案選(2)

以上的寫法計算量有些龐大，可善用「變數變換」及「對稱性」，簡化計算過程：

先找出 \(x+\frac{\pi}{6}\) 及 \(sinx\) 的中點：
$$\frac{(x+\frac{\pi}{6})+x}{2} = x+\frac{\pi}{12}$$ 接著令 \(y= x+\frac{\pi}{12}\)，其中 \(\frac{\pi}{12}\leq y < 2\pi+\frac{\pi}{12}\)。此時方程式可改寫 $$sin(y+\frac{\pi}{12})=sin(y-\frac{\pi}{12})+\frac{1}{2}$$
利用和角公式展開
$$
sinycos\frac{\pi}{12}+cosysin\frac{\pi}{12} = sinycos\frac{\pi}{12}-cosysin\frac{\pi}{12}+\frac{1}{2}
$$
移項整理，並且將 \(sin\frac{\pi}{12}\) 換成 \(\frac{\sqrt{6}-\sqrt{2}}{4}\)
$$cosy\cdot \frac{\sqrt{6}-\sqrt{2}}{4} = \frac{1}{4}\ \Longrightarrow \ cosy = \frac{\sqrt{6}+\sqrt{2}}{4}=cos\frac{\pi}{12}$$ 最後在限制範圍內解得 $$y=\frac{\pi}{12}, \ 2\pi-\frac{\pi}{12} \ \ 兩解 $$ 因此答案選(2)

單選第5題：組合與中位數(中偏難)

這一題結合了中位數與組合的觀念，我將題意以下圖呈現可能會清楚一些：

設甲組的中位數為 \(a\)，乙組的中位數為 \(a+1\)，在 \(a\) 之前有12個數字，\(a+1\) 之前除了 \(a\) 之外也有12個數字。
另外，在 \(a\) 之後除了 \(a+1\) 之外有12個數字，在 \(a+1\) 之後也有12個數字。

也就是說，前面24個數字中(1~24)，必須被分成兩組各12個數，方法數為 \(C^{24}_{12}\)；
同樣道理，後面24個數字中(27~50)，必須被分成兩組各12個數，方法數為 \(C^{24}_{12}\)。

由於將數字分組被拆成兩個步驟，因此要用乘法原理，共有分法 \((C^{24}_{12})^2\) ，答案選 (4)。

單選第6題：三角測量(中偏難)

這種三角測量題的第一步就是要先將圖畫出來：

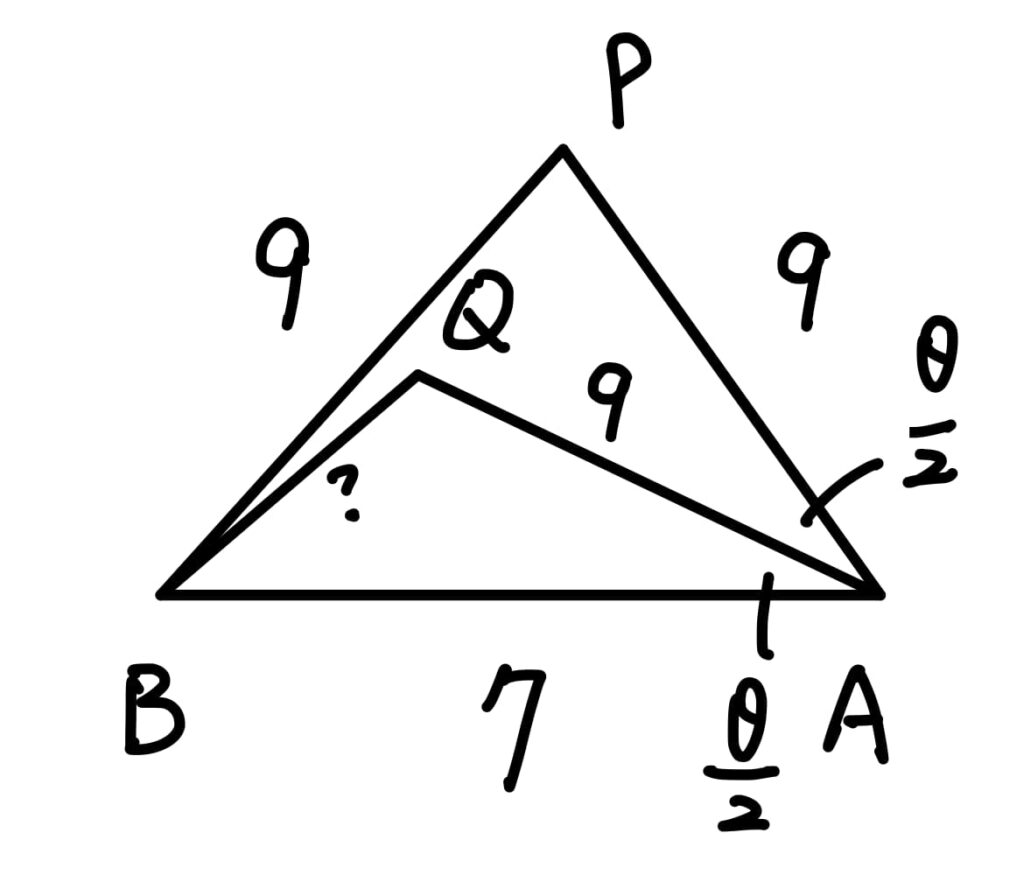
在 \(\Delta ABC\) 中，先以餘弦定理算出 \(\cos\theta\)：$$cos\theta = \frac{7^2+9^2-9^2}{2\times 7 \times 9}= \frac{7}{18}$$

利用餘弦函數的半角公式 $$cos\frac{\theta}{2}=\sqrt{\frac{1+\cos\theta}{2}}=\sqrt{\frac{1+\frac{7}{18}}{2}}=\frac{5}{6}$$

在 \(Delta ABQ\) 中，再針對 \(\angle{BAQ}\) 用一次餘弦定理
$$\overline{BQ}=\sqrt{7^2+9^2-2\times 7\times 9\times \frac{5}{6}}=5$$ 因此答案選(3)

多選第7題：對數函數的圖形(易)

這一題是基礎題，唯一要注意的是選項(2)。

選項(1)：錯誤$$y+\frac{1}{2}=log5+logx$$ 與 圖形 \(\Gamma\) 不同。
備註：這個選項有一些爭議，\(y+\frac{1}{2}\) = log(5x) 只是 \(y=logx\) 平移的結果，那麼我們說這兩個圖形完全相同似乎也沒有問題，待後續大考中心的回覆。

選項(2)：錯誤$$2y=2log|x|$$
要注意的是，真數 \(x\) 上的次方是偶數次，當次方拿到前面時，記得要加上絕對值，避免真數為負的情形。
選項(3)：正確 $$3y=3logx$$
與選項(2)不同的是，真數 \(x\) 上的次方是奇數次。由\(x^3>0\)，必定保證 \(x>0\)，因此真數不須再加絕對值。
選項(4)：正確$$y=logx \Longleftrightarrow x=10^y$$
選項(5)：錯誤 $$x^3=(10^y)^3=10^{3y}$$ 因此答案選(3)(4)

多選第8題：等差數列與三角形的面積綜和題(中等難度)

選項(1)：由 $$n^2+(n+1)^2-(n+2)^2 = n^2-2n-3 = (n-3)(n+1)$$ 可知 \(T_2\) 是鈍角三角形，此選項錯誤。

選項(2)：令 \(T_n\) 的周長為 \(S_n:=3n+3, n\geq 2\)，故 \(S_n\) 形成公差為 \(3\) 的等差數列，此選項正確。

選項(3)：利用海龍公式可知 $$T_n \ 的面積 = \sqrt{\frac{3n+3}{2}\cdot\frac{n+3}{2} \cdot \frac{n+1}{2} \cdot \frac{n-1}{2}}$$ 顯然隨 \(n\) 增大而增大，此選項正確。

選項(4)：設 \(T_5\) 三邊上的高分別為 \(h_5，h_6，h_7\)，則
$$ 5\cdot h_5 = 6\cdot h_6 = 7\cdot h_7 = 2\cdot T_5 \ 的面積:=2\Delta $$ 故
$$h_5=\frac{2\Delta}{5}， \ h_6=\frac{2\Delta}{6}， \ h_7=\frac{2\Delta}{7}$$ 不是等差數列，此選項錯誤。

選項(5)：因為 $$3^2+4^2=5^2 \ \ 且 \ \ 2^2+3^2<4^2$$ 所以 \(T_3\) 的最大角為直角，\(T_2\) 的最大角為鈍角，

因此 \(T_3\) 的最大角應該小於 \(T_2\) 的最大角，此選項錯誤。答案選 (2)(3)。

多選第9題：迴歸直線的基本觀念(中等難度)

迴歸直線的問題很好掌握，主要就兩個重點：
1. 迴歸直線必定過資料的算術平均數 2. 迴歸直線的斜率＝相關係數 × 兩資料標準差的比值。

選項(1)：
$$\begin{aligned}
\overline{y_A} &= 2\overline{x_A} – 0.6 = 2\times 5.2 – 0.6 = 9.8 \\
\overline{y_B} &= 1.5\overline{x_B} + 0.4 = 1.5\times 6 + 0.4 = 9.4
\end{aligned}$$ 即 \(\overline{y_A}>\overline{y_B}\)，此選項錯誤。

選項(2)：分別從兩直線的斜率看出 \(A\) 物種及 \(B\) 物種的標準差。
$$\begin{aligned}
2 &= m_A = 0.6 \times \frac{\sigma_A^y}{0.3} \Rightarrow \sigma_A^y=1 \\
1.5 &= m_B = 0.3 \times \frac{\sigma_B^y}{0.1} \Rightarrow \sigma_B^y=0.5
\end{aligned}$$
即 \(A\) 物種的體重標準差大於 \(B\) 物種的體重標準差。此選項錯誤。

選項(3)：$$|個體P的體重 – \overline{y_A}|=|8.6-9.8|=1.2>1$$ 此選項正確。

選項(4)：設 \(P(5.6, 8.6)\)，則
$$\begin{aligned}
d(P,L_A) &= \frac{|2\times 5.6 – 8.6 -0.6|}{\sqrt{5}} = \frac{2}{\sqrt{5}} \\
d(P,L_B) &= \frac{3\times 5.6 – 2\times 8.6 + 0.8}{\sqrt{13}}= \frac{0.4}{\sqrt{13}}
\end{aligned}$$
因此 $$d(P,L_A)>d(P,L_B)$$ 此選項錯誤。

選項(5)：設 \(P(5.6, 8.6)\)、\(A(\overline{x_A}, \overline{y_A})\)、\(B(\overline{x_B},\overline{y_B})\)
$$\begin{aligned}
\overline{PA}^2 &= 0.4^2 +1.2^2 \\
\overline{PB}^2 &= 0.4^2+ 0.8^2
\end{aligned}$$ 故 $$\overline{PA}^2>\overline{PB}^2$$ 此選項錯誤，答案選(3)。

多選第10題：平面向量(中等難度)

首先，我們先將圖畫出來看一下：

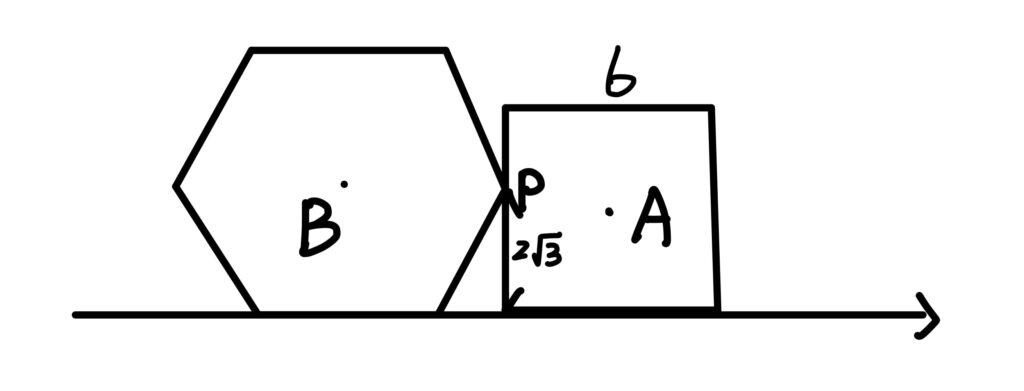
可以看出來，點\(A\)到 \(x\) 軸的距離為\(3\) “小於” 點\(B\)到 \(x\) 軸的距離 \(2\sqrt{3}\)，此選項錯誤。

選項(2)：如下圖所示

直角\(\Delta CDP\) 的內角\(\angle{PCD}=60^{\circ}\)，且\(\overline{PD}=2\sqrt{3}\)，故\(\overline{PC}=4\)，
此選項錯誤。

選項(3)：我們將圖形座標化如下：

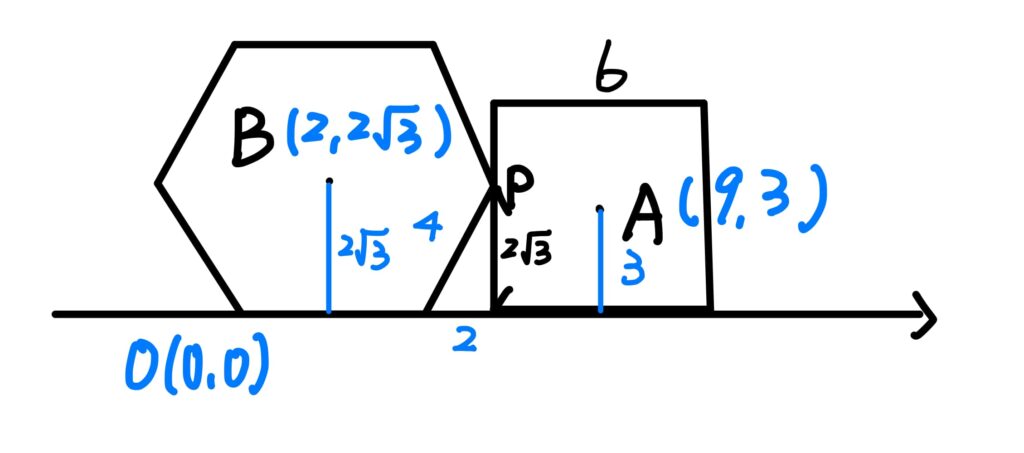
因此向量 $$\overrightarrow{BA}=(7,3-2\sqrt{3})$$ 此選項正確。

選項(4)：先寫出點\(P\)的座標 \(P(6,2\sqrt{3})\)

$$\overline{AP}^2=3^2+(3-2\sqrt{3})^2=30-12\sqrt{3}\approx 9.24 < 10$$ 此選項錯誤。

選項(5)：$$m_{AP}=\frac{3-2\sqrt{3}}{9-6}=\frac{3-2\sqrt{3}}{3}=\frac{\sqrt{3}-2}{\sqrt{3}}>-\frac{1}{\sqrt{3}}$$ 此選項正確。因此答案選 (3)(5)

多選第11題：機率與二元一次聯立方程式綜合題(中偏難)

這一題是「二元一次聯立方程式」與「機率」的混合題，可以使用克拉瑪公式輔助解題。

按題意，$$a=1、2、3、4、5、6，b=1、2$$

選項(1)：$$p(a=b)=\frac{2}{C^6_2\cdot C^2_1}=\frac{1}{6}$$ 此選項錯誤。

選項(2)：此方程組無解的充要條件為 $$\frac{a}{1}=\frac{6}{b}\neq \frac{6}{1}$$ 即
$$ab=6，b\neq 1$$ 僅有 \(a=3, b=2\) 唯一一種情形，因此機率 $$p=\frac{1}{12}$$ 此選項正確。

選項(3)：此方程組有唯一組的充要條件為 $$\frac{a}{1}\neq \frac{6}{b}$$ 即 $$ab\neq 6$$ 故
$$p(ab\neq 6) = 1-p(ab=6) = 1-\frac{2}{12}=\frac{5}{6}$$ 此選項正確。

選項(4)：硬幣出現反面，則 \(b=2\)；此方程組無解，則 \(a\neq 3\)，故
$$p(a\neq 3, b=2)=\frac{5}{12}$$

選項(5)：$$x=\frac{\Delta_x}{\Delta}>0$$ 其中
$$\Delta = \left|\begin{matrix}
a & 6 \\
1 & b
\end{matrix}\right|\ ,
\Delta_x=\left|\begin{matrix}
6 & b \\
1 & b
\end{matrix}\right|
$$ 即 $$\frac{6b-6}{ab-6}>0$$ 將 \(b=2\) 代入可得 $$\frac{6}{2a-6}>0$$ 即 $$a>0$$
因此 $$p(x>0\ | \ b=2, a\neq 3)=p(a>3|b=2\ ,\ a\neq 3)=\frac{3/12}{5/12}=\frac{3}{5}$$ 此選項錯誤。
最後答案選(2)(3)

多選第12題：平面上的線性變換(中等難度)

選項(1)：
$$TA = \left[\begin{matrix}
3 \\
0
\end{matrix}\right] ,
TB = \left[\begin{matrix}
0 \\
1
\end{matrix}\right] ,
TC = \left[\begin{matrix}
-3 \\
0
\end{matrix}\right]
$$ 將這個圖形畫出來

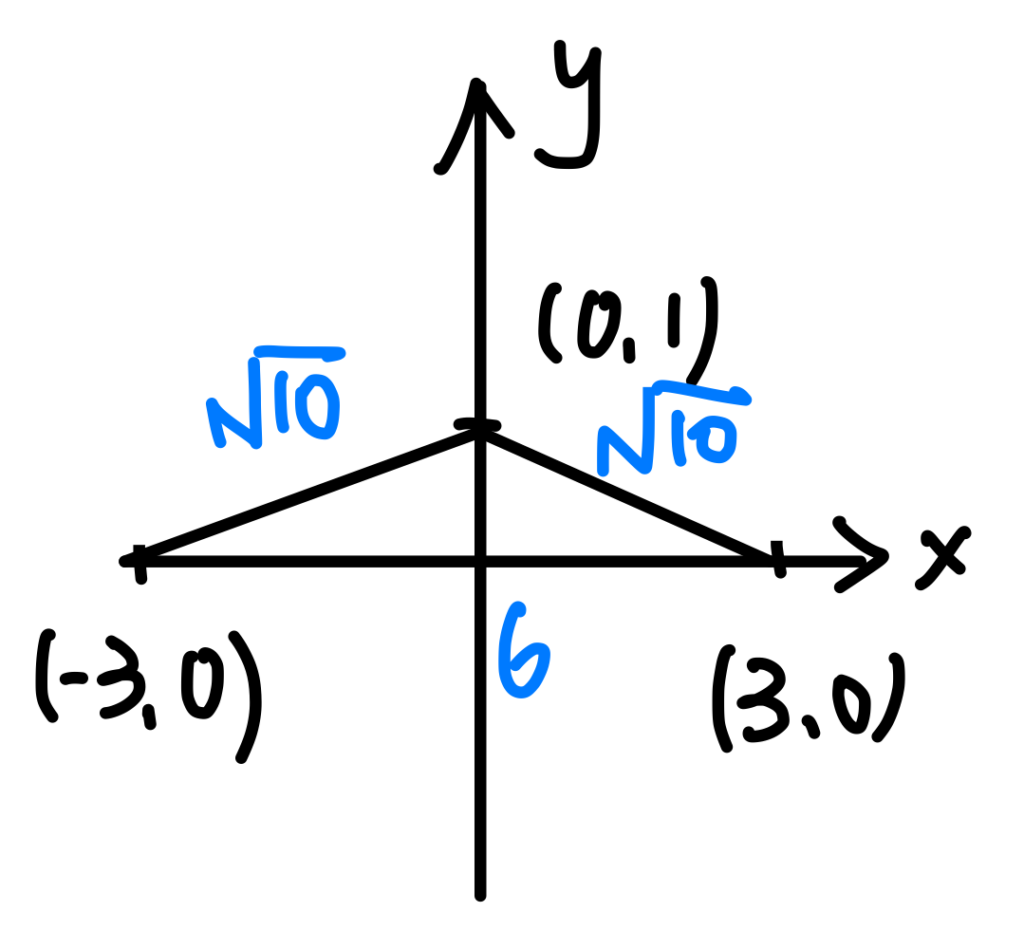
因為 $$\sqrt{10}^2 + \sqrt{10}^2 – 6^2 <0 $$ 所以 \(\Gamma\) 是等腰鈍角三角形才對，此選項錯誤。

選項(2)：要判斷是否有點 \((x,y)\) 滿足
$$\begin{bmatrix}
3 & 0 \\
a & 1
\end{bmatrix}\cdot\begin{bmatrix}
x \\
y
\end{bmatrix}=
\begin{bmatrix}
x \\
y
\end{bmatrix}$$ 整理可得
\begin{cases}
3x = x \\
ax+y=y
\end{cases} 可解得 $$x=0$$ 因此在 \(\Delta ABC\) 的邊上，只有兩點 \((0,0)、(0,1)\) 經 \(T\) 變換後坐標不變。此選項正確。

選項(3)：先寫下經由轉換後三點的坐標如下：
$$TA = \left[\begin{matrix}
3 \\
0
\end{matrix}\right] ,
TB = \left[\begin{matrix}
0 \\
1
\end{matrix}\right] ,
TC = \left[\begin{matrix}
-3 \\
-a
\end{matrix}\right]
$$

當 \(a=0\) 時，\(\Gamma\) 不會有部分落在第四象限。

選項(4)：按題意可知
$$T^{-1}\cdot\begin{bmatrix}
1 & 0 & -1 \\
0 & 1 & 0
\end{bmatrix}=
\frac{1}{3}\begin{bmatrix}
1 & 0 & -1 \\
a & 1 & a
\end{bmatrix}
$$ 將等號兩邊同乘以 \(T\) 可得
$$\begin{bmatrix}
1 & 0 & -1 \\
0 & 1 & 0
\end{bmatrix}=
T\cdot\begin{bmatrix}
\frac{1}{3} & 0 & -\frac{1}{3} \\
\frac{a}{3} & \frac{1}{3} & \frac{a}{3}
\end{bmatrix}
$$ 也就是說，可以找到一個三角形，三頂點分別為 \((\frac{1}{3},\frac{a}{3}),\ (0, \frac{1}{3}),\ (-\frac{1}{3}, \frac{a}{3}) \) 經 \(T\) 變換後為 \(\Delta ABC\)，此選項正確。

選項(5)：$$|\Gamma| = |T|\cdot \Delta ABC 的面積 = 3\times \Delta ABC 的面積 $$ 即 \(\Gamma\) 的面積為定值。

多選第13題：三元一次聯立方程式(易)

這一題非常簡單，依題意，可列出以下三元一次聯立方程式：
$$\begin{cases}
100A+400B+240C = 260(A+B+C) \\
100A+400B = 280(A+B)
\end{cases}$$

將以上方程式化簡可得
\begin{cases}
8A-7B+C=0 \tag{13.1} \\
3A = 2B
\end{cases}

設 \(A=2r, B=3r\) 代入方程式 \((3.1)\) 可得 $$16r-21r+C=0$$ 解得 $$C=5r$$ 因此 $$A:B:C=2:3:5$$

選填第14題：多項式的除法(中等難度)

依除法原理列式如下：

$$
設\begin{cases}
f(x)=(x^2-2x+3)Q_1(x) + x+1 \\
g(x)=(x^2-2x+3)Q_2(x) + x-3 \\
h(x)=(x^2-2x+3)Q_3(x)-2
\end{cases}
$$
接著計算
$$
xf(x)+ag(x)+bh(x) \\
= (x^2-2x+3)(xQ_1(x)+aQ_2(x)+bQ_3(x))+x(x+1)+a(x-3)-2b
$$
其中 $$x(x+1)+a(x-3)-2b = x^+(a+1)x-3a-2b$$ 可以被 \(x^2-2x+3\) 整除。
因此
$$\begin{cases}
a+1 = -2 \\
-3a-2b=3
\end{cases}$$
解得
$$\begin{cases}
a=-3 \\
b=3
\end{cases}$$

選填第15題：期望值(中等難度)

首先，先確定有幾顆摸彩球：設共有 \(n\) 顆摸彩球，則
$$\frac{10}{n}=\frac{0.4}{100} \Longrightarrow n=2500$$

接著，依題意及期望值的定義直接計算：
$$E=\frac{C^4_1}{2400}\times 5000 + \frac{C^5_1}{2400}\times 8000 = \frac{300}{12} = 25$$

選填第16題：平面向量的正射影長(中偏難)

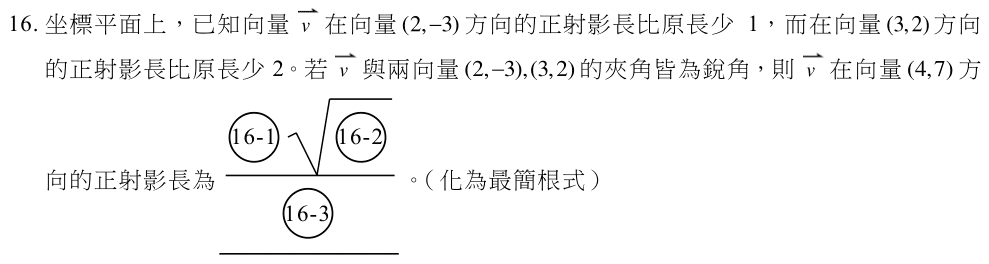
這一題非常精彩，是這份考題中，兩道難題中的其中一題。不妨依題意先畫個簡圖如下：

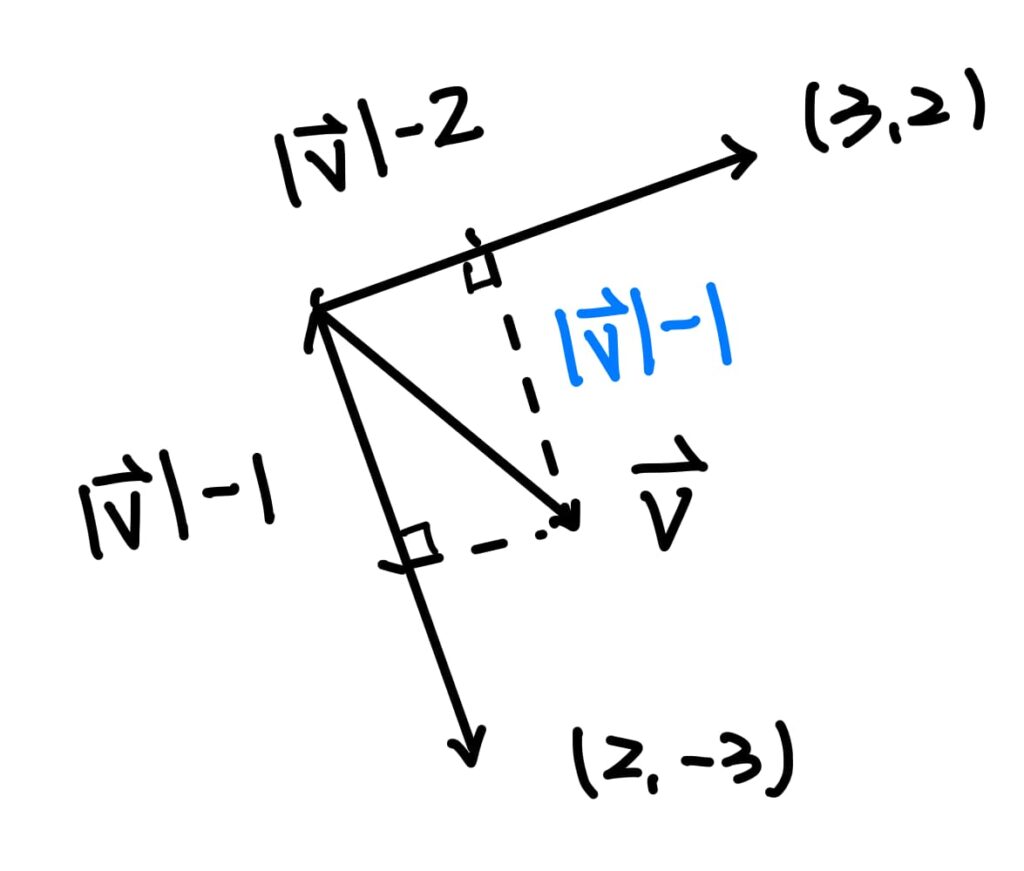
這一題的關鍵在於，題目給的那兩個向量 \((2, -3)、(3,2)\) 互相垂直。
因此可以使用畢氏定理先求出向量\(\overrightarrow{v}\) 的長度：
$$
|\overrightarrow{v}|^2 = (|\overrightarrow{v}|-1)^2+(|\overrightarrow{v}-2|)^2 \tag{16.1}
$$將方程式 (16.1) 展開整理後可得 $$|\overrightarrow{v}|^2-6|\overrightarrow{v}|+5=0$$
接著因式分解 $$(|\overrightarrow{v}|-1)(|\overrightarrow{v}|-5)=0$$
可解得 $$|\overrightarrow{v}|=5 \ 或\ 1 (不合) $$

接下來，將向量 \((4,7)\)寫成向量 \((2,-3)\) 及 \((3,2)\) 的線性組合如下：
$$(4,7) = -(2,-3) + 2(3,2)$$
計算向量\(\overrightarrow{v}\)與向量\((4,7)\) 的內積
$$\begin{aligned}
\overrightarrow{v}\cdot (4,7) &= -\overrightarrow{v} \cdot (2,-3) + 2\overrightarrow{v}\cdot (3,2) \\
&= -\sqrt{13}\cdot 4 +2\sqrt{13}\cdot 3 = 2\sqrt{13}
\end{aligned}$$ 最後，我們就可以計算向量\(\overrightarrow{v}\)在向量\((4,7)\) 的正射影長了：
$$\frac{|\overrightarrow{v}\cdot (4,7)|}{\sqrt{65}}=\frac{2\sqrt{13}}{\sqrt{65}}=\frac{2\sqrt{5}}{5}$$

選填第17題：二元一次不等式經典試題(難)

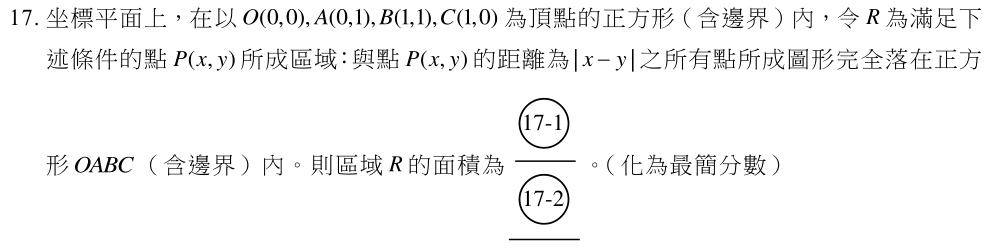
這一題應該是整份試卷最難的一題了，連題目都不容易看懂，先畫個圖來觀察一下：

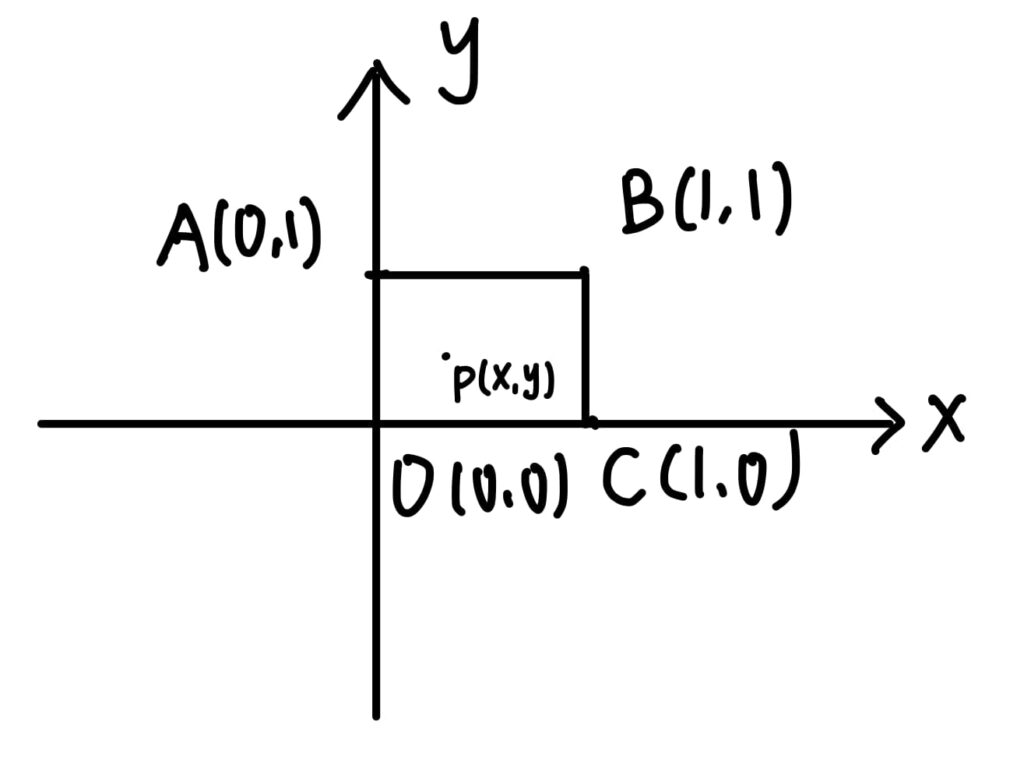
換個說法應該比較好理解一點：以 \(P\) 點為圓心，\(|x-y|\) 為半徑畫圓，
而這個圓必須落在正方形 \(OABC\) (含邊界) 內：那麼這個半徑不能超過 \(P\) 點至四條邊界的距離，

可列式如下：
$$\begin{cases}
|x-y|\leq y \\
|x-y|\leq x \\
|x-y|\leq 1-y \\
|x-y|\leq 1-x
\end{cases}$$
接著分情況討論如下：

情況1. \(x=y\)
\begin{cases}
y \geq 0 \\
x \geq 0 \\
y \leq 1 \\
x \leq 1
\end{cases}圖形就是此正方程的對角線

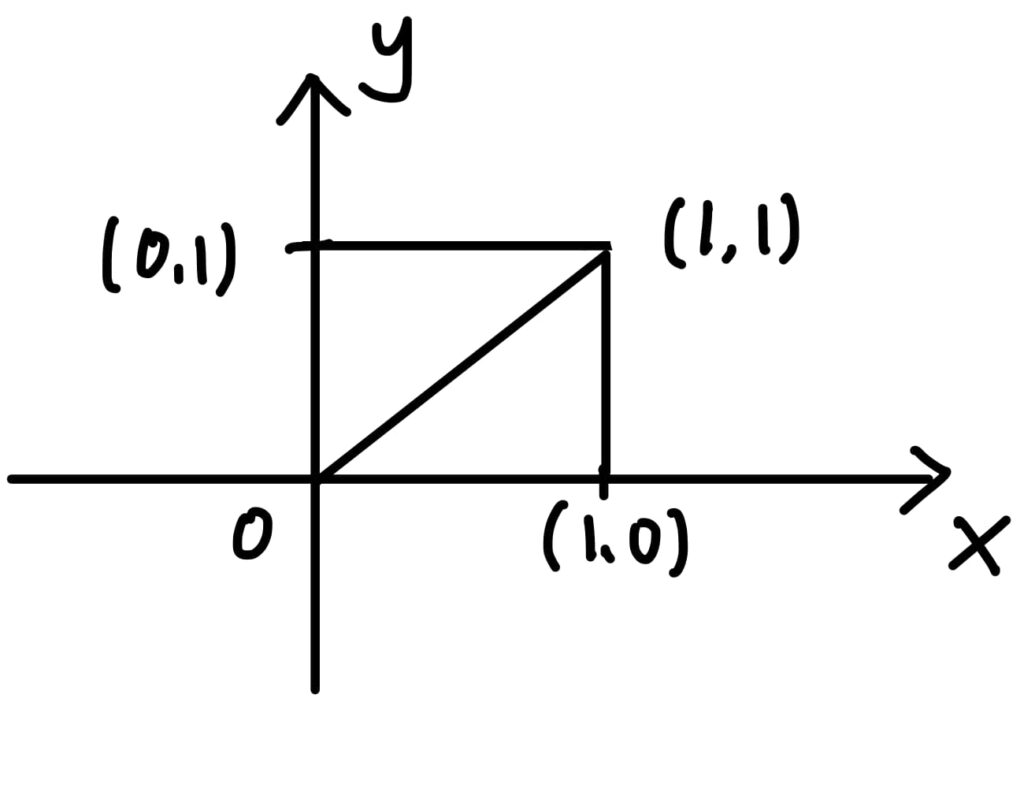
情況2. \(x-y>0\)，將聯立方程式改寫如下
\begin{cases}
x \leq 2y \\
y \geq 0 \\
x \leq 1\\
y \geq 2x-1
\end{cases} 再將此圖形畫上去

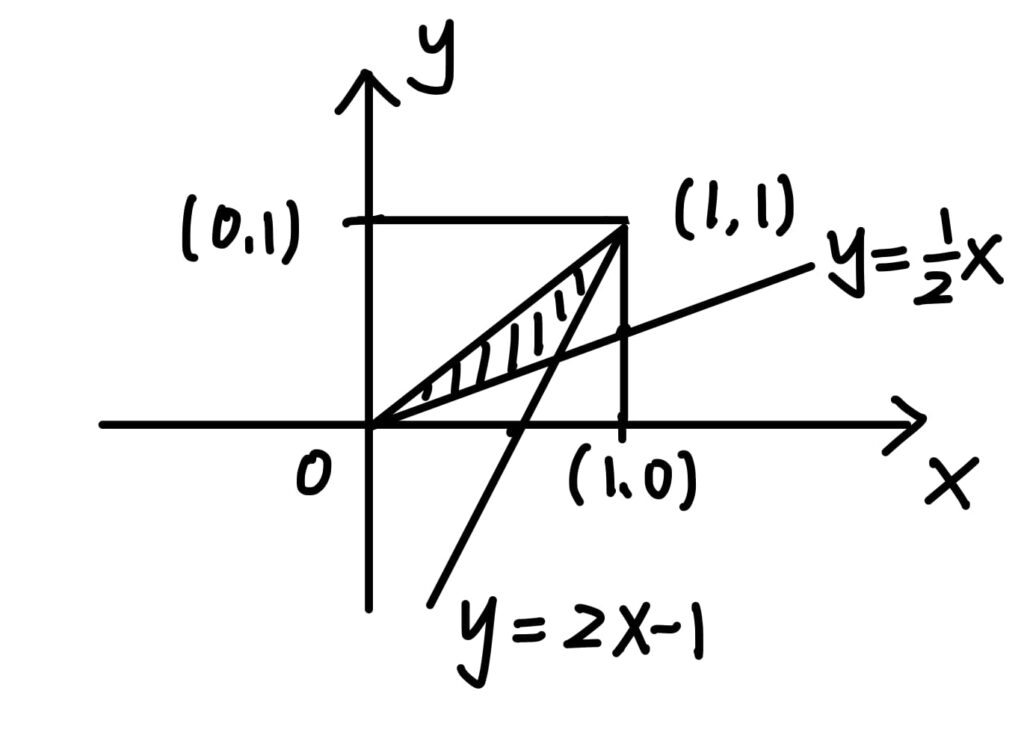
情況3. \(x-y<0\)，再將聯立方程式改寫如下：
$$\begin{cases}
x\geq 0 \\
2x-y \geq 0 \\
x-2y \geq -1 \\
y \leq 1
\end{cases}$$
再畫圖

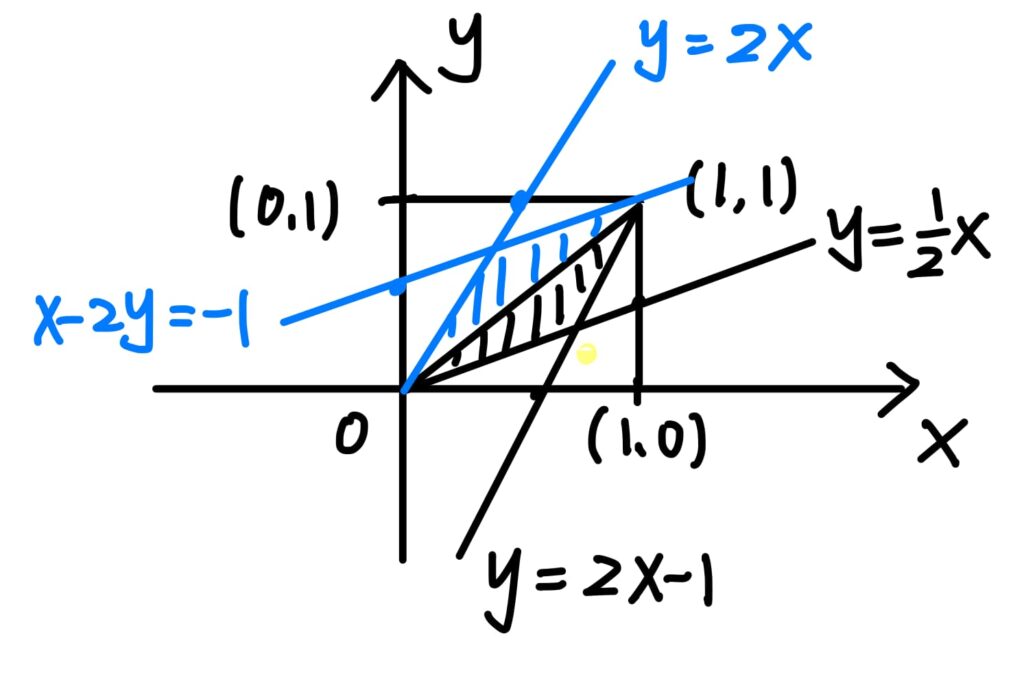
斜線部份是一個平行四邊形
$$面積 =
\begin{Vmatrix}
\frac{2}{3} &1 \\
\frac{1}{3} & 1
\end{Vmatrix}=\frac{1}{3}$$

題組第18題：兩向量的夾角(易)

題組題不難，可以輕鬆解決。

先畫個圖來看一下：

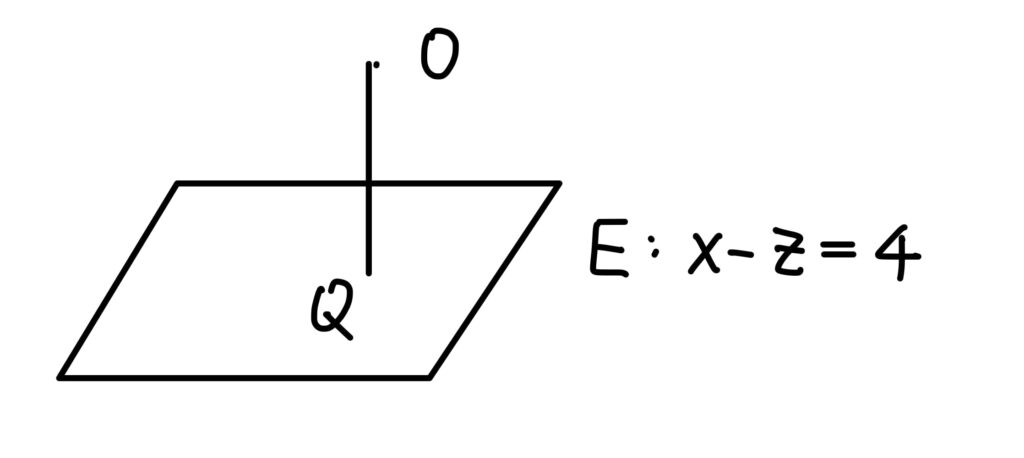
向量 \(\overrightarrow{OQ}\) 平行平面 \(E\) 的法向量 \((1,0,-1)\)，因此 $$cos\alpha = \frac{(1,0,-1)\cdot(1,0,0)}{\sqrt{2}\cdot 1}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$$ 答案選(4)

題組第19題：向量的內積(中等難度)

直接用內積的定義處理：
$$cos\theta = \frac{(a,b,c)\cdot (1,0,0)}{|\overrightarrow{OP}\cdot 1|}= \frac{a}{\sqrt{a^2+b^2+c^2}} \tag{19.1}$$

因為 \(\theta \leq \frac{\pi}{6}\) 且 餘弦函數在區間 \([0,\pi]\) 為遞減函數，所以
$$cos\theta \geq cos\frac{\pi}{6}=\frac{\sqrt{3}}{2}$$

因此式子 (19.1) 中，$$\frac{a}{\sqrt{a^2+b^2+c^2}}\geq \frac{\sqrt{3}}{2}$$
將不等式兩邊平方可得
$$\frac{a^2}{a^2+b^2+c^2}\geq \frac{3}{4}$$ 移項整理可得
$$a^2\geq 3(b^2+c^2)$$ 得證。

題組第20題：二次函數求極值(中等難度)

因為 \(P\in E:x-z=4\)，則 $$a-c=4$$
承19題，將\(b=0\) 代入不等式 \(a^2 \geq 3(b^2+c^2)\) 中，並且將 \(c\) 代換成 \(a-4\) 可得，
$$a^2\geq 3c^2 \geq 3(a-4)^2 \tag{20.1}$$

將方程式(20.1)展開整理：
$$a^2-12a+24\leq 0 \tag{20.1}$$ 解不等式(20.1) 可得
$$6-2\sqrt{3}\leq a \leq 6+2\sqrt{3}$$

最後計算 \(\overline{OP}^2\)：
$$\overline{OP}^2=a^2+c^2=a^2+(a-4)^2=2a^2-8a+16=2(a-2)^2+8$$

將此二次函數的圖形畫出來看一下：

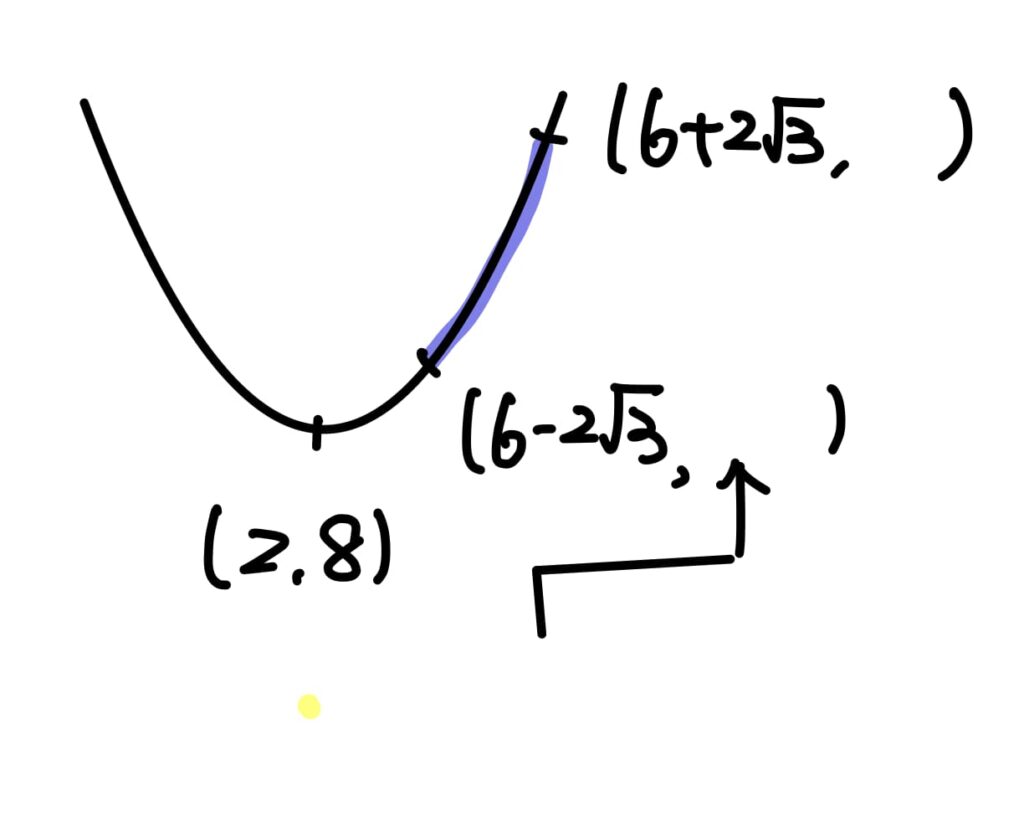
要注意討論範圍並沒有包含頂點，最小值發生在 \(x=6-2\sqrt{3}\) 的地方，代入計算
$$\overline{OP}^2=2(4-2\sqrt{3})^2+8=64-32\sqrt{3}=64-2\sqrt{768}=(4\sqrt{3}-4)^2$$
因此，$$\overline{OP}\geq 4\sqrt{3}-4$$

這份詳解就寫到這邊，提供給有需要的人參考。
如果你對於高中數學學習相關主題有興趣，歡迎留下姓名與e-mail接收相關主題的訊息。

筆者簡介