課程回顧

高中數學第一冊介紹了「數系」，將數的家族做了簡單的分類，到了高三介紹了「複數」，擴充了我們對於數的認知。國中時，我們所遇到的所有數，都是「實數」。但是，一旦遇到某些特定的方程式，我們便找不到相對應的數表示其解。例如：$$x^2=-1$$

國中時，我們都稱這樣的方程式為無解。更一般地說，如果二次方程式$$ax^2+bx+c=0$$的判別式 $$D=b^2-4ac<0$$ 則這個方程式，便稱為無解。

在十六世紀時，義大利數學家卡丹諾(Girolamo Cardano, 1501~1576)研究三次方程式的公式解時，曾提出了一道問題：

將10分成兩個數，使其乘積為40

雖然卡丹諾對於這樣的數有所疑慮，但仍試著對其進行運算：

假設其中一個數為 \(x\)，則另一個數為 \(10-x\)，依題意可知 $$x(10-x)=40$$ 整理後可得
$$x^2-10x+40=0$$ 可以配方法解得 $$x=5+\sqrt{-15} \ \ or \ \ 5-\sqrt{-15}$$

後來經過許多數學家的努力，設法賦予 \(\sqrt{-1}\) 的意義，直到數學家歐拉(1707~1783) 引入了虛數單位 $$i=\sqrt{-1}$$實數系因而可以擴展到了複數系，這一思想的演進，耗費了200年左右的時間，這可不是一件容易的事。

後來數學家高斯(Carl Friedrich Gauss, 1777~1855)更進一步證明了多項式方程式在複數系中都可以找到解。

有了複數的概念後，我們就可以將任何數表示成 $$a+bi$$ 的形式，其中 \(a,b\) 都是實數，而且\(a\) 稱為「實部」、\(b\) 稱為「虛部」。這便是我們在課堂上，較多著墨的代數形式。

然而，在十九世紀末，有關複數的研究，大多走向了幾何解釋的道路。

其幾何表徵，就是將複數 \(a+bi\) 對應到直角坐標平面上的一個點 \((a,b)\)，而這個點與原點連線，
就可以用來表示平面上的有向線段(向量)。

$$a+bi \longleftrightarrow \ 點P(a,b) \ \longleftrightarrow \ 向量\overrightarrow{OP}=(a,b)$$

也就是說，複數 \(z=a+bi\) 可以看成是坐標平面上的向量 \(\overrightarrow{OP}=(a,b)\)

那麼，兩複數的運算所代表的幾何意義是什麼呢？

複數運算的幾何意義

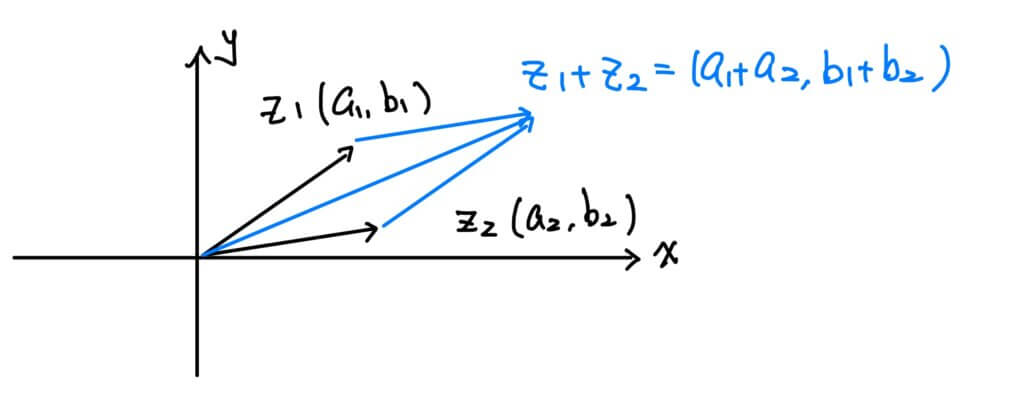
首先，我們設兩複數為 \(z_1=a_1+b_1i\) 及 \(z_2=a_2+b_2i\) 在直角坐標平面上分別對應到向量 \((a_1,b_1)\) 及 向量 \((a_2,b_2)\)，則
$$z_1+z_2 = (a_1+a_2) + (b_1+b_2)i$$ 可對應到向量$$(a_1+a_2, b_1+b_2)$$ 這就是我們所熟悉的向量的加法，其相加的方式稱為「平行四邊形法則」，在幾何上就是「平移」的意思。

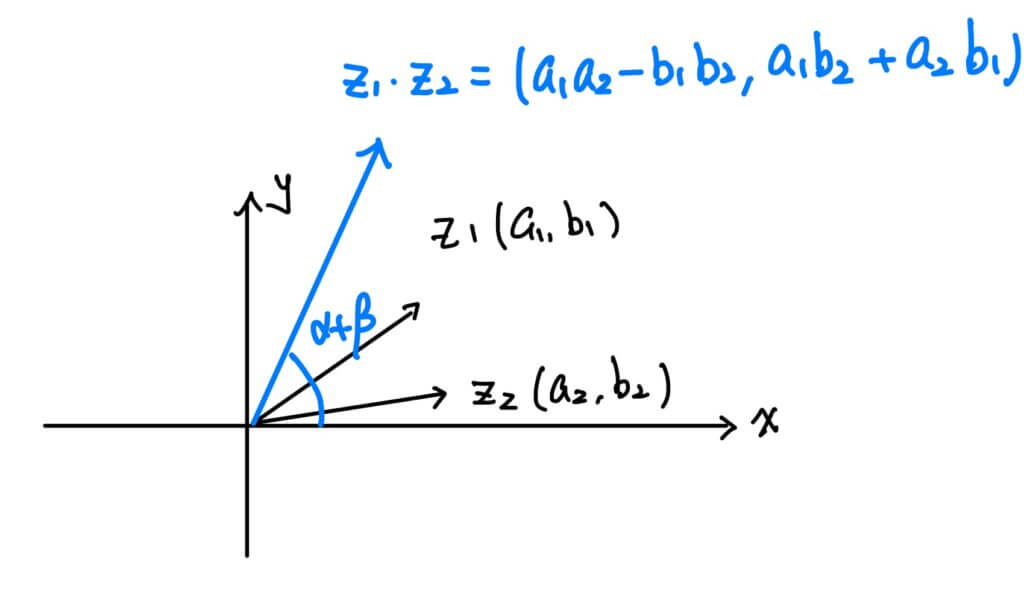
另外，兩複數相乘呢？$$z_1\cdot z_2 = (a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i$$ 可對應到向量 $$(a_1a_2-b_1b_2, a_1b_2+a_2b_1)$$ 我們可以將直角坐標改寫為極坐標的形式方便觀察

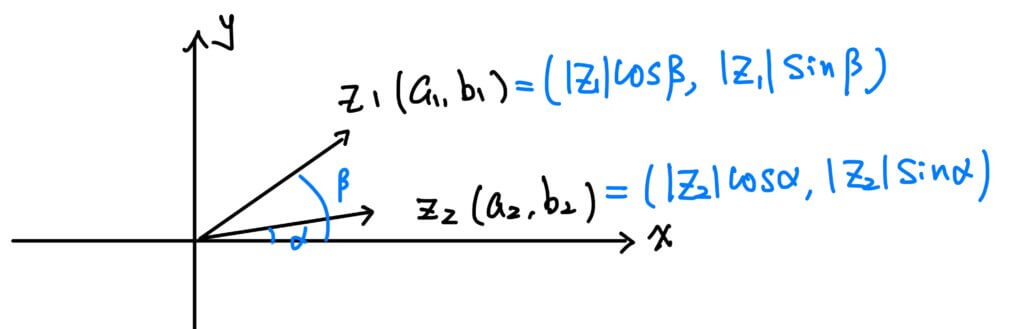
設
$$(a_1, b_1) = (|z_1|cos\beta, |z_1|sin\beta), \ (a_2, b_2) = (|z_2|cos\alpha, |z_2|sin\alpha)$$ 則
$$\begin{cases}
a_1a_2-b_1b_2 = |z_1||z_2|cos\alpha cos\beta-|z_1||z_2|sin\alpha sin\beta = |z_1||z_2|cos(\alpha+\beta) \\
a_1b_2+a_2b_1=|z_1||z_2|sin\alpha cos\beta + |z_1||z_2|sin\alpha sin\beta = |z_1||z_2|sin(\alpha+\beta)
\end{cases}$$ 也就是說，兩複數相乘，表示向量 \((a_2, b_2)\) 的長度變為 \(|z_1||z_2|\)，並且逆時針旋轉 \(\beta\) 角度。

以上的操作方式，可以用來推導隸美弗定理，以及解出任何複數的 \(n\) 次方根，這在教科書中都有詳細的介紹。

接下來要問的是，如果是空間向量，是否可以用複數來表示呢？

四元數(Quaternion)的誕生

我們前面已經知道，給定某向量的坐標，如何用另一組坐標來表示此向量「伸縮及旋轉」後的結果。

但是這樣的想法，到了空間向量卻發生了困難。平面向量有2個分量，空間向量有3個分量。

愛爾蘭數學家漢彌爾頓(Sir William Wowan Hamilton, 1805-1865) 提出了解決方法：3個分量行不通，要有4個分量，
但必須犧牲乘法交換律才行。要將空間中的一個向量作旋轉，必須繞一個固定的軸，
而表示此固定軸的方向要有2個量(例如經緯度)，向量繞軸旋轉的角度是1個量，長度的伸縮是1個量，
因此這樣的新數要有4個分量而非3個。

漢彌爾頓稱這樣的數為四元數(quarternions)。

任何四元素皆可表示成 $$d+ai+bj+ck$$ 其中 \(a,b,c,d\) 為實數，\(d\) 稱為「純量」部分，其餘部分稱為「向量」部分。向量部分 \((a,b,c)\) 為空間直角坐標系中某一點的坐標。而 \(i,j,k\) 稱為定性單位(qualitative unit)，在幾何上即是直角坐標系的三個坐標軸的方向。也就是說， $$i=(1,0,0),\ j=(0,1,0), \ k=(0,0,1)$$ 滿足
$$i^2 = j^2 = k^2 = -1$$ 且 $$ij=k, ji=-k, jk=i, kj=-i, ki=j, ik=-j$$ 這裡用的其實就是我們高中學到的外積的運算規則。外積與內積其中一個差異就是，外積沒有交換律。

接下來以平面向量的做法，可以寫出兩空間向量的加減法，並且得知此運算所代表的幾何意義為平移。

那麼四元數的乘法又會如何呢？

設兩個四元數 $$u=d+ai+bj+ck, v=w+xi+yj+zk$$ 可得
$$\begin{aligned}
uv &= (d+ai+bj+ck)(w+xi+yj+zk) \\
&= (dw-ax-by-cz) +i(aw+dx+bz-cy) + j(bw+dy+cx-az) + k(cw+dz+ay-bx)
\end{aligned}$$

可以看出兩個四元數相乘後依然是四元數。如果令純量 \(d=0\)，就是我們所熟知的空間向量。
再由四元數的乘法可得 $$uv = -(ax+by+cz) +i(bz-cy) + j(cx-az) + k(ay-bx) $$

觀察「純量」與「向量」的部分，可以定義出向量的兩種乘積，分別是「內積」
$$\overrightarrow{u}\cdot\overrightarrow{v} = ax+by+cz$$ 可用來解釋兩向量的夾角與正射影。

與「外積」
$$\overrightarrow{u}\times \overrightarrow{v}=(bz-cy)i+(cx-az)j+(ay-bx)k$$ 代表的意義就是與兩向量垂直的向量。

這一篇文章預設是給高中生作為課內知識的延伸學習，不宜過度論述及太多技術操作的細節，就先寫到這邊。
如果對這樣的主題有興趣想要更進一步了解，可參考另一篇文章：旋轉矩陣，當中就有提及三維空間的旋轉矩陣、歐拉角等相關主題。

---

歡迎訂閱 高中數學數位學習電子報

---