前言

八年級時，我們第一次學到了「畢氏定理」，這個定理告訴我們，一個直角三角形的兩股平方和等於斜邊的平方。文獻上記載，畢氏定理有超過三百多種的證明方式。其中，歐幾里德的風車證法堪稱經典。到了高一下學期，我們學到了三角比的應用之一：「餘弦定理」。這一篇文章，我們要從風車證法中，觀察餘弦定理修正項出現的原因。雖然證明過程相較課本教我們的方式複雜一些，也沒有這麼直觀，但卻更可以看出餘弦定理修正項與幾何的連結。

畢氏定理的證明方法：歐幾里德的風車證法

首先，我們考慮以下這個圖形：

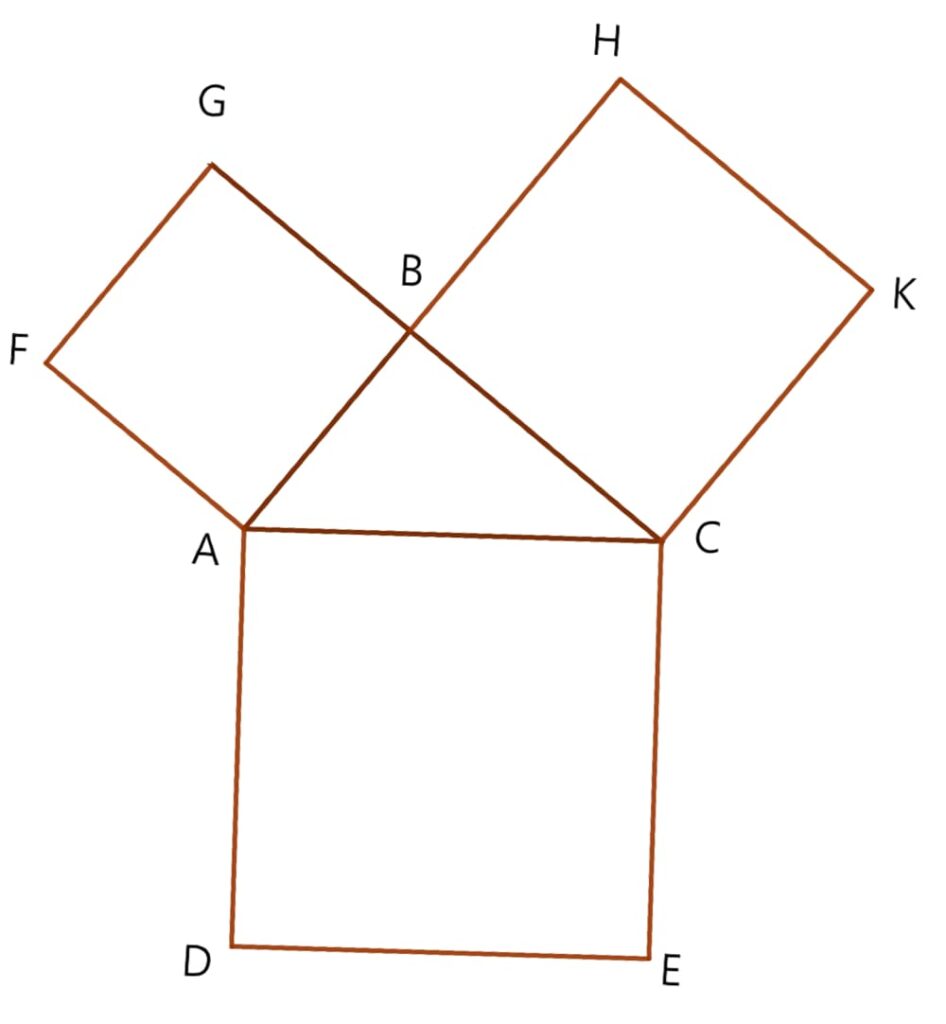
其中$\Delta ABC$為直角三角形，且 $\angle{ABC}=90^{\circ}$，以其三邊長往外延展出三個正方形 $ABGF$、$ACED$、$BCKH$。

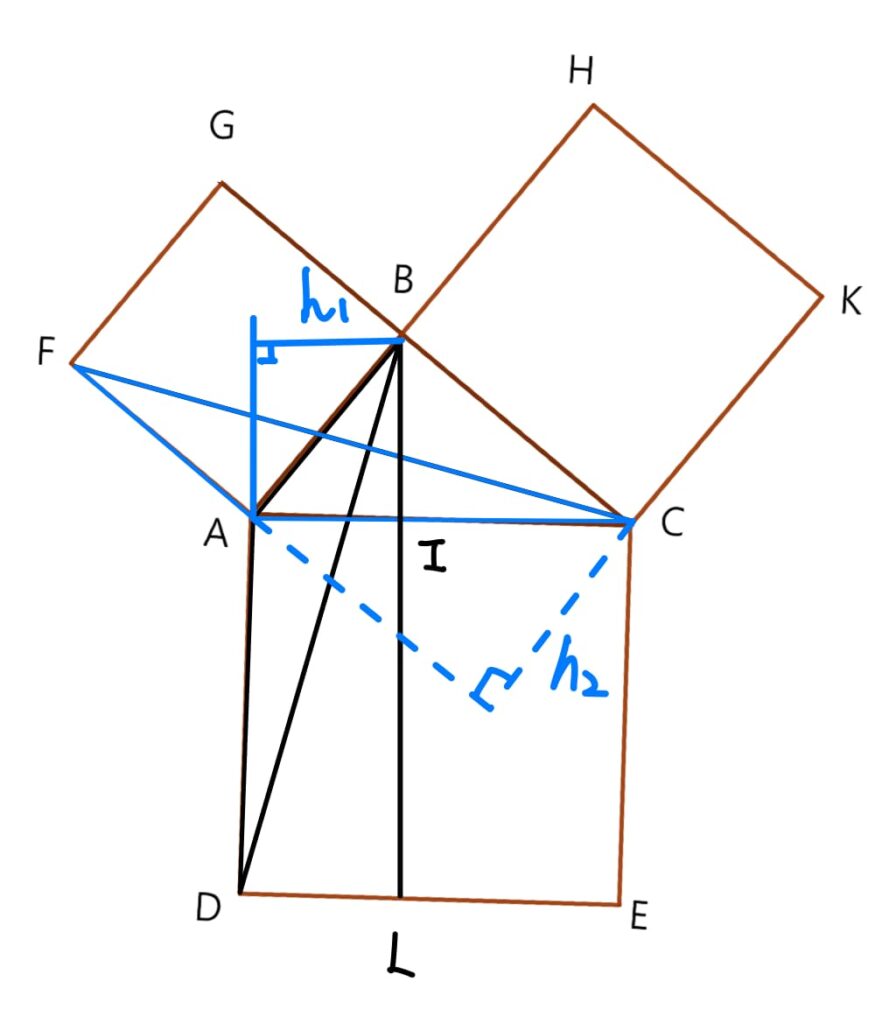
連接$CF$、$BD$，並且過$B$點做鉛直線，分別交$\overline{AC}$與$\overline{DE}$於$I$、$L$兩點(如下圖)。

稍微觀察一下，不難發現 $\Delta ACF \cong \Delta ADB (SAS)$，先來計算 $\Delta ABD的面積$

$$\begin{aligned} \Delta ABD面積 &= \overline{AD}\times h_1 \times \frac{1}{2} \\ &= 矩形ADLI的面積 \times \frac{1}{2} \end {aligned}$$

另一方面，計算 $\Delta ACF的面積$

$$\begin{aligned} \Delta ACF的面積 &= \overline{AF}\times h_2 \times \frac{1}{2} \\ &= 正方形ABGF的面積 \times \frac{1}{2} \end {aligned}$$ 因為 $\Delta ABD面積\cong \Delta ACF的面積$，所以 $$矩形ADLI的面積 = 正方形ABGF的面積$$

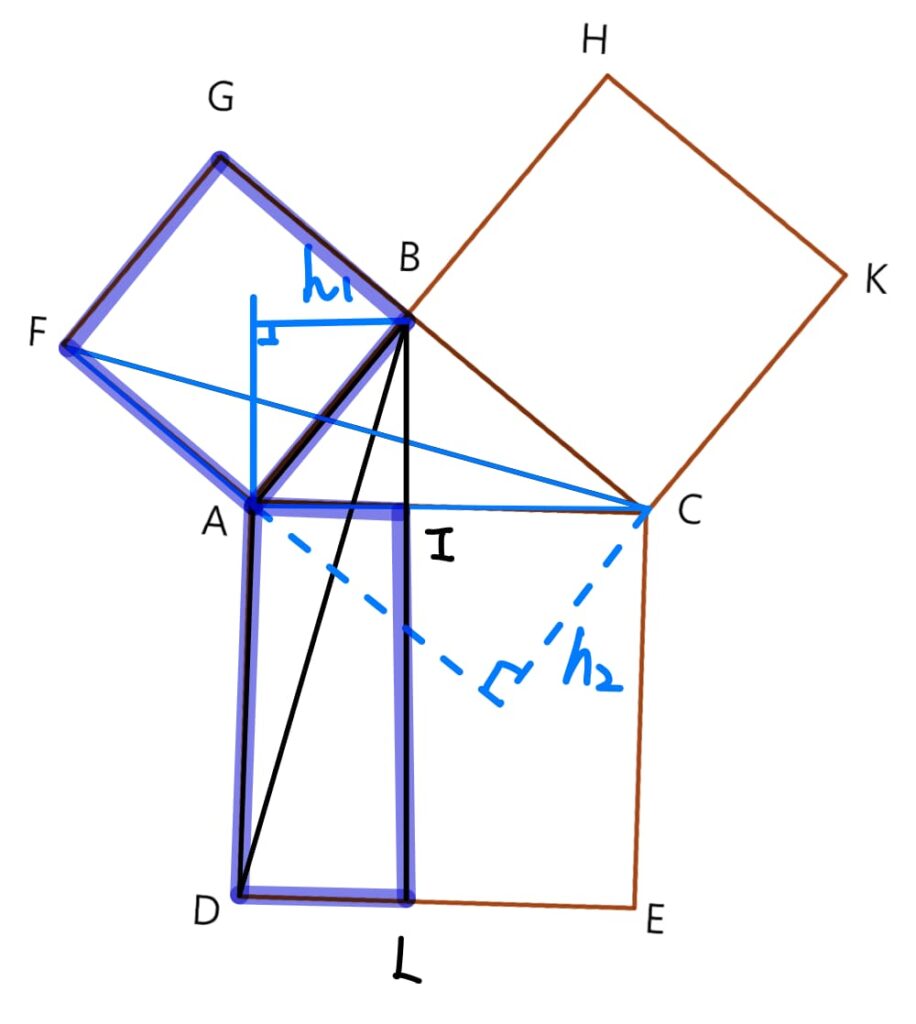
同理，

$$矩形ILEC的面積=正方形BCKH的面積$$

因此，

$$\begin{aligned} 正方形ADEC的面積 &= 矩形 ADLI的面積 + 矩形ILEC的面積 \\ &= 正方形ABGF的面積 ＋ 正方形BCKH的面積 \end{aligned}$$ 亦即 $$\overline{AC}^2=\overline{AB}^2+\overline{BC}^2$$ 得證。

回顧課程：餘弦定理

什麼是餘弦定理？敘述如下：在 $\Delta ABC$ 中，$\angle A, \angle B,\angle C$ 的對邊長分別為 $a,b,c$，則

$$\begin{aligned} a^2 &= b^2+c^2 -2bccosA \\ b^2 &= a^2+c^2 -2accosB \\ c^2 &= a^2+b^2 -2abcosC \\ \end{aligned}$$

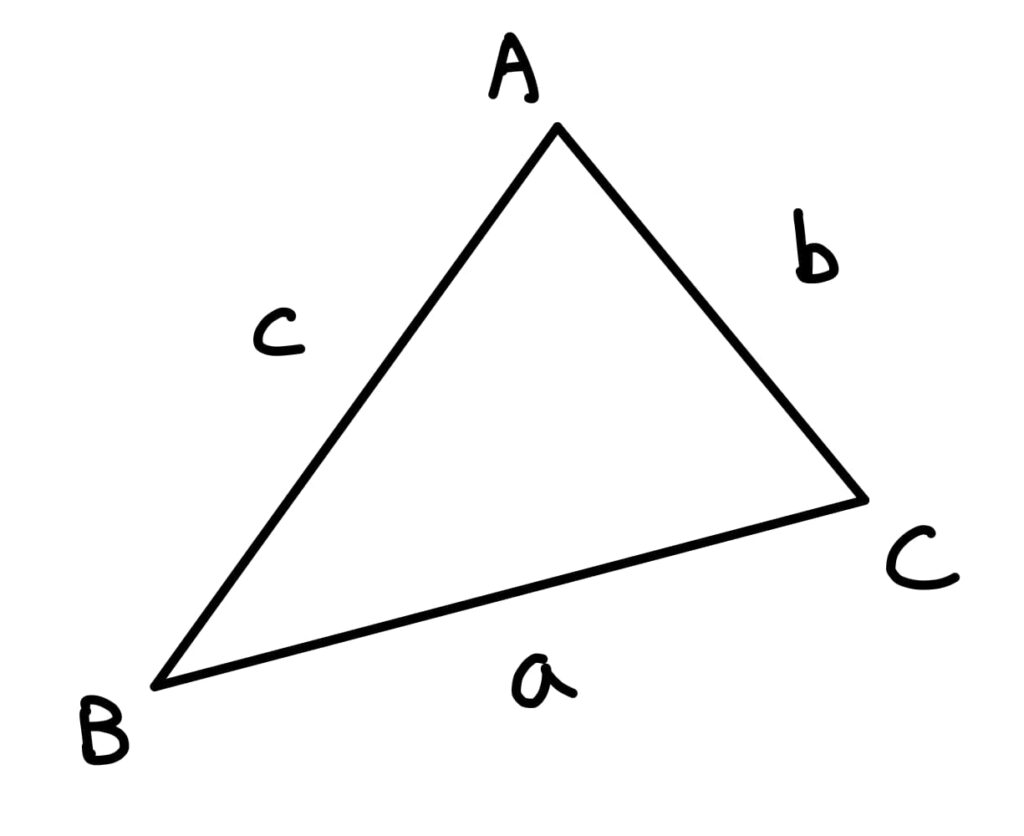
目前教科書提供的證明，主要為代數操作，快速地來複習一下：

第一個方法，作$BC$ 邊上的高 $\overline{AD}$。

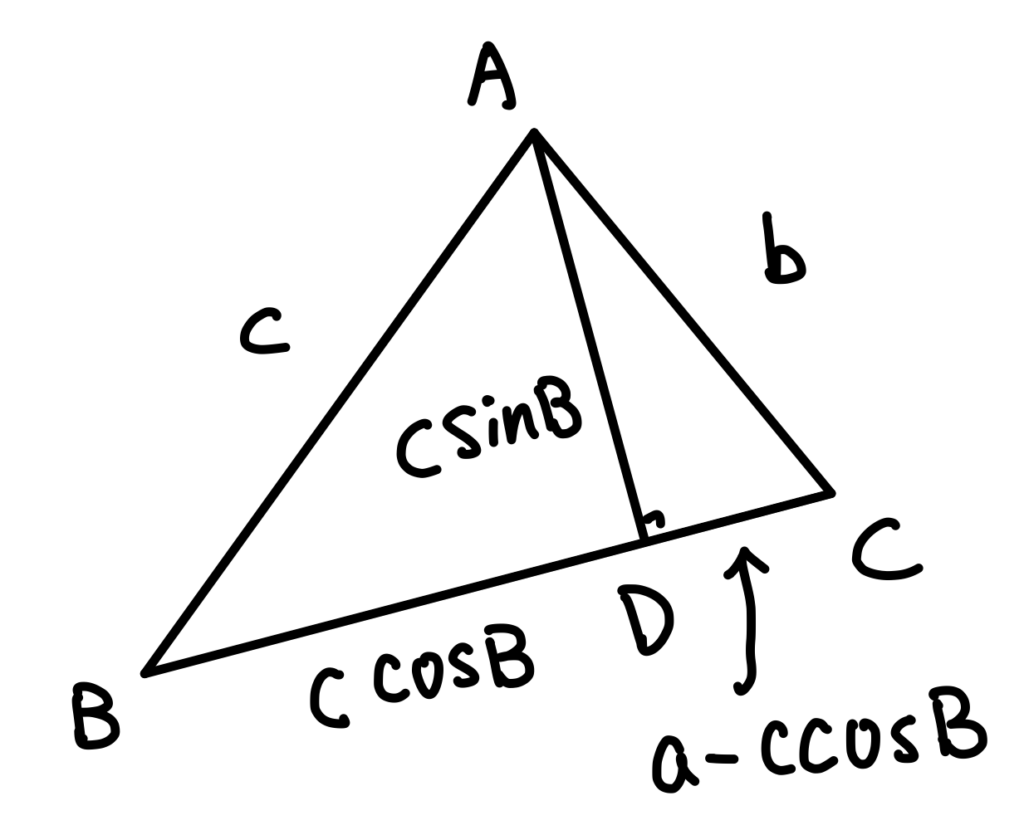
在 $\Delta ABD$中，$\overline{BD}=ccosB, \overline{AD}=csinB$，

因此，在$\Delta ACD$中，$\overline{CD}=a-ccosB$，根據畢氏定理

$$\begin{aligned} b^2 &= (a-ccosB)^2+(csinB)^2 \\ &= a^2+c^2-2accosB \end{aligned}$$ 這是很簡單的代數證明。

另一個方式則是使用解析幾何，建立坐標系：以 $B$ 為原點，$\overleftrightarrow{BC}$ 為 $x$ 軸。

標上3個頂點坐標後，寫出 $A$、$C$兩點的距離

$$\begin{aligned} b^2&=\overline{AC}^2 \\ &=(a-ccosB)^2+(csinB)^2 \\ &= a^2+c^2(cos^2B+sin^2B)-2accosB \\ &= a^2+c^2-2accosB \end{aligned}$$

從以上兩個證明，我們可以看出，餘弦定理的本質其實還是畢氏定理，修正項在代數運算的過程中自然出現了。接下來我們來看看歐幾里德的風車證法中，修正項的幾何意義。

餘弦定理的證明方法：歐幾里德的風車證法

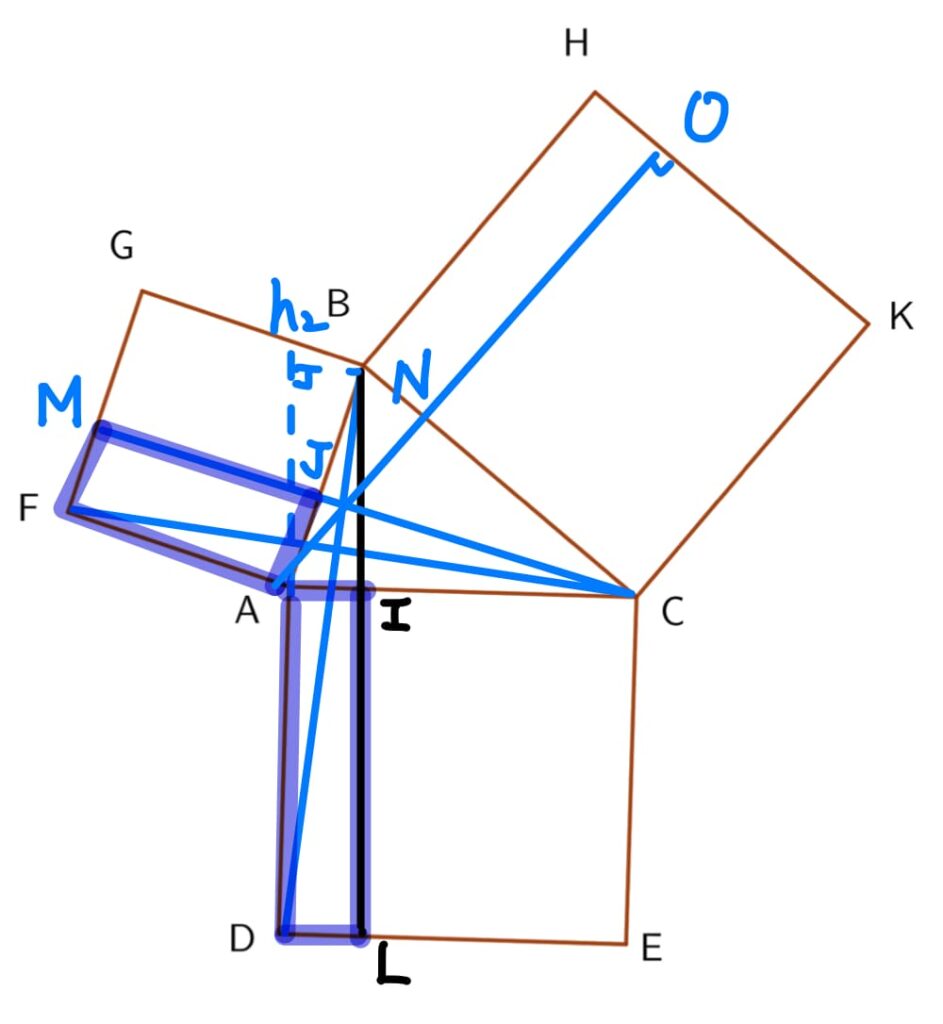
考慮 $0^{\circ}<\angle{B}<90^{\circ}$ ($\angle{ABC}>90^{\circ}$的情形留給讀者練習)，如下圖所示：

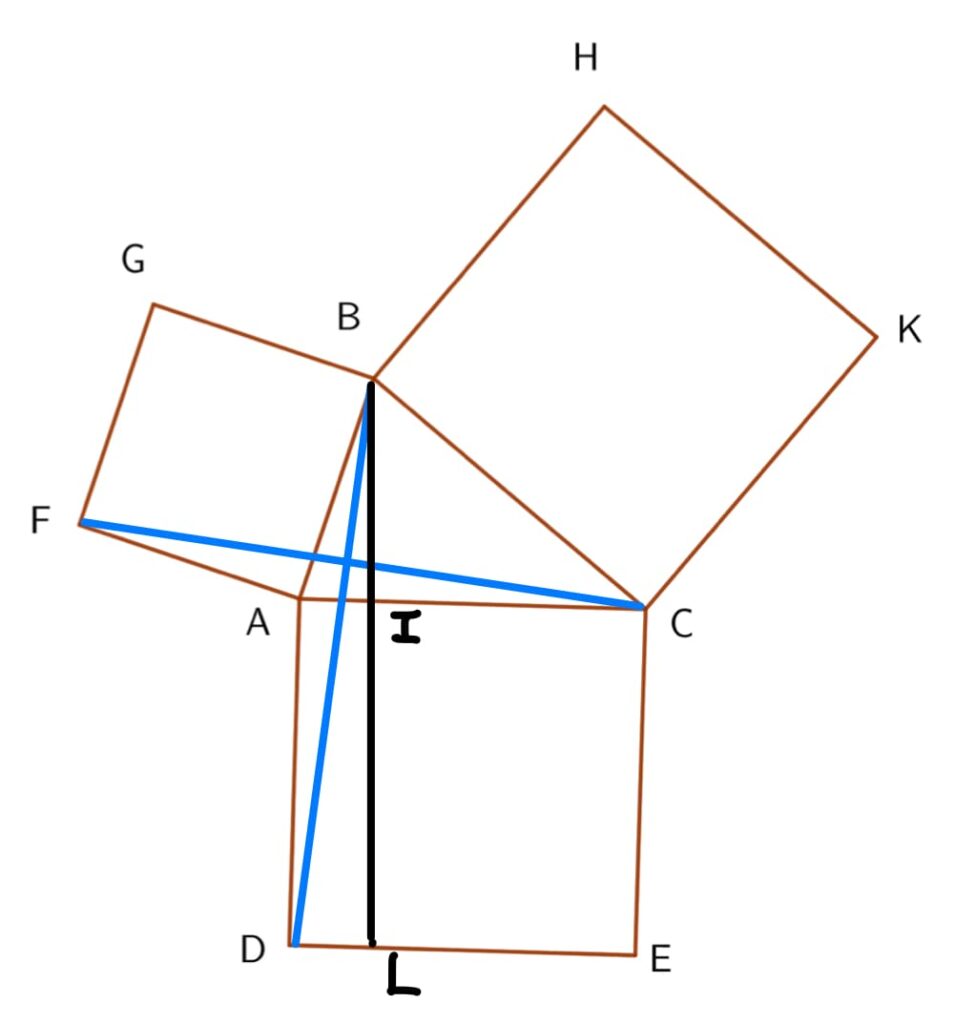
顯然，$\Delta AFC \cong \Delta ABD (SAS)$。

接著，分別計算 $\Delta AFC$ 及 $\Delta ABD$ 的面積

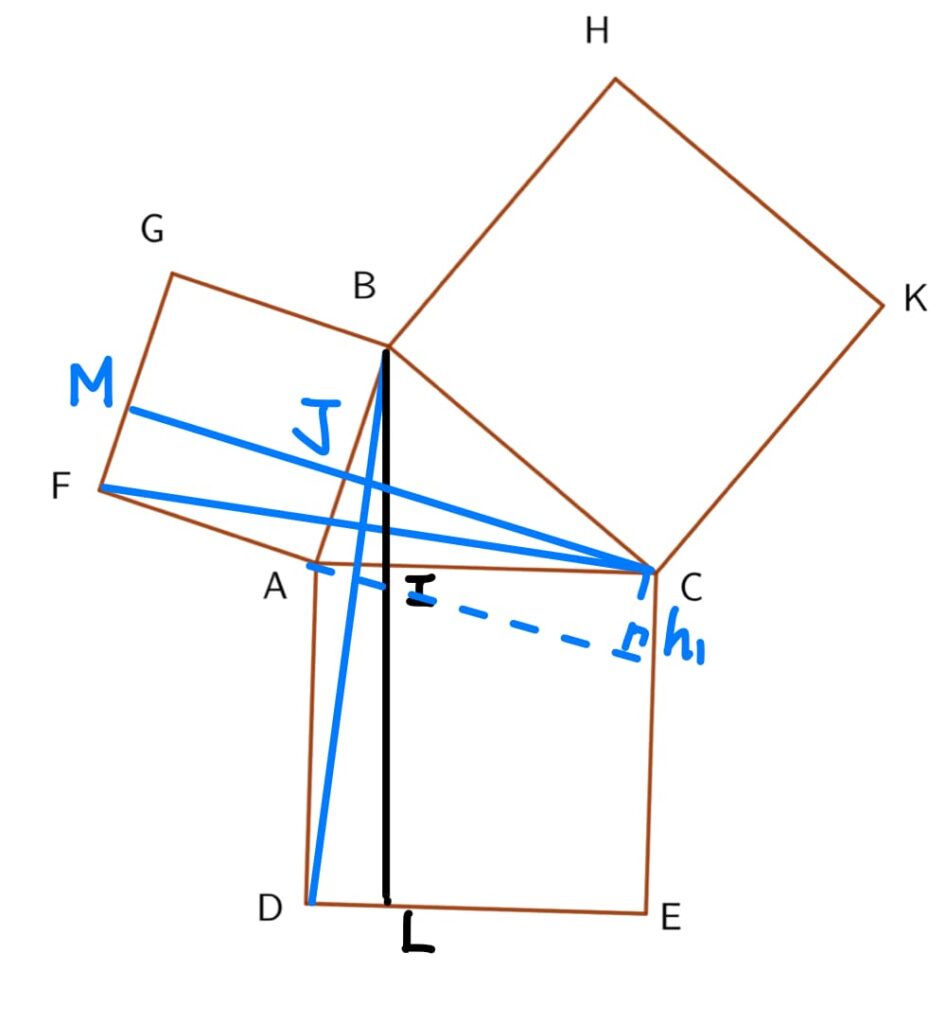
$$\begin{aligned} \Delta AFC的面積 &= \overline{AF}\times h_1 \times \frac{1}{2}\\ &= 矩形 AFMJ的面積 \times \frac{1}{2} \end{aligned} \tag{1}$$

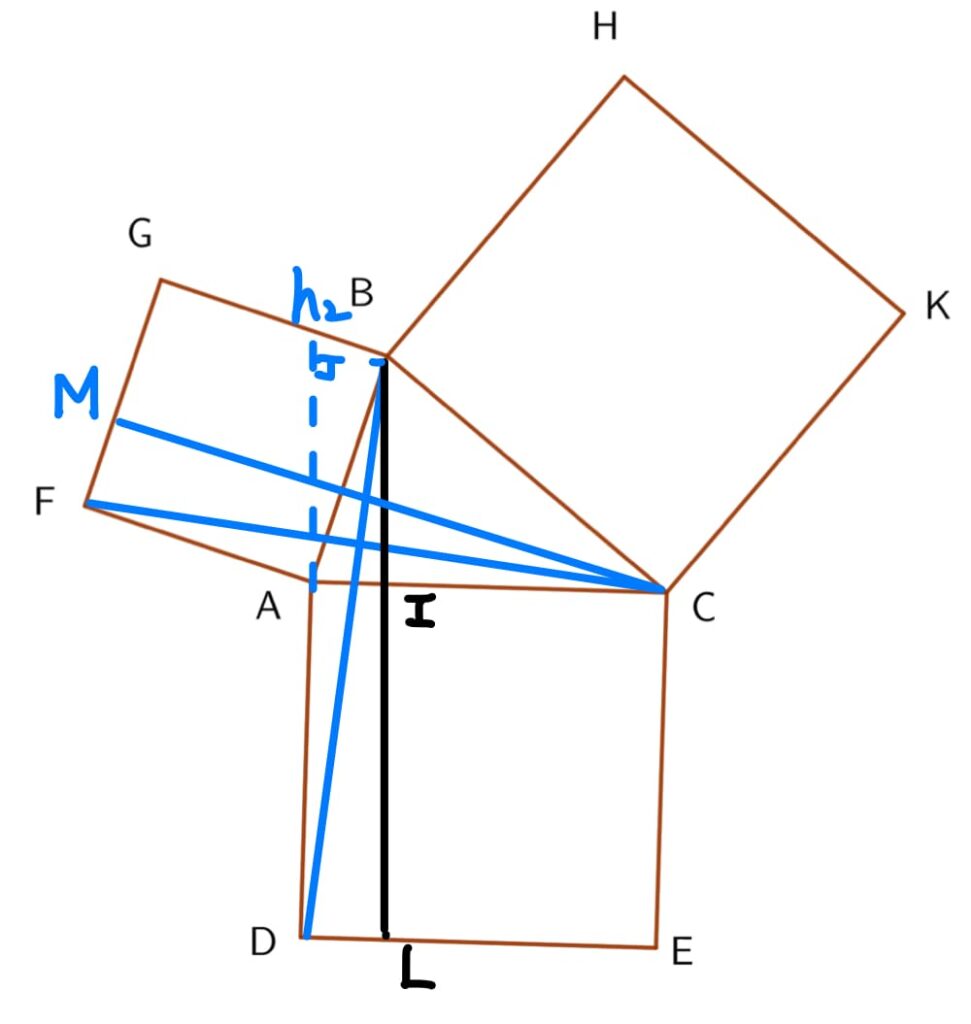
$$\begin{aligned} \Delta BAD 的面積 &= \overline{AD} \times h_2 \times \frac{1}{2} \\ &= 矩形ADLI的面積 \times \frac{1}{2} \end{aligned} \tag{2}$$
因為 $\Delta AFC \cong \Delta ABD (SAS)$，所以由第(1)式及第(2)式可知，$矩形AFMJ的面積 = 矩形 ADLI的面積$

同理，

$$矩形CNOK的面積 = 矩形 ILEC的面積$$

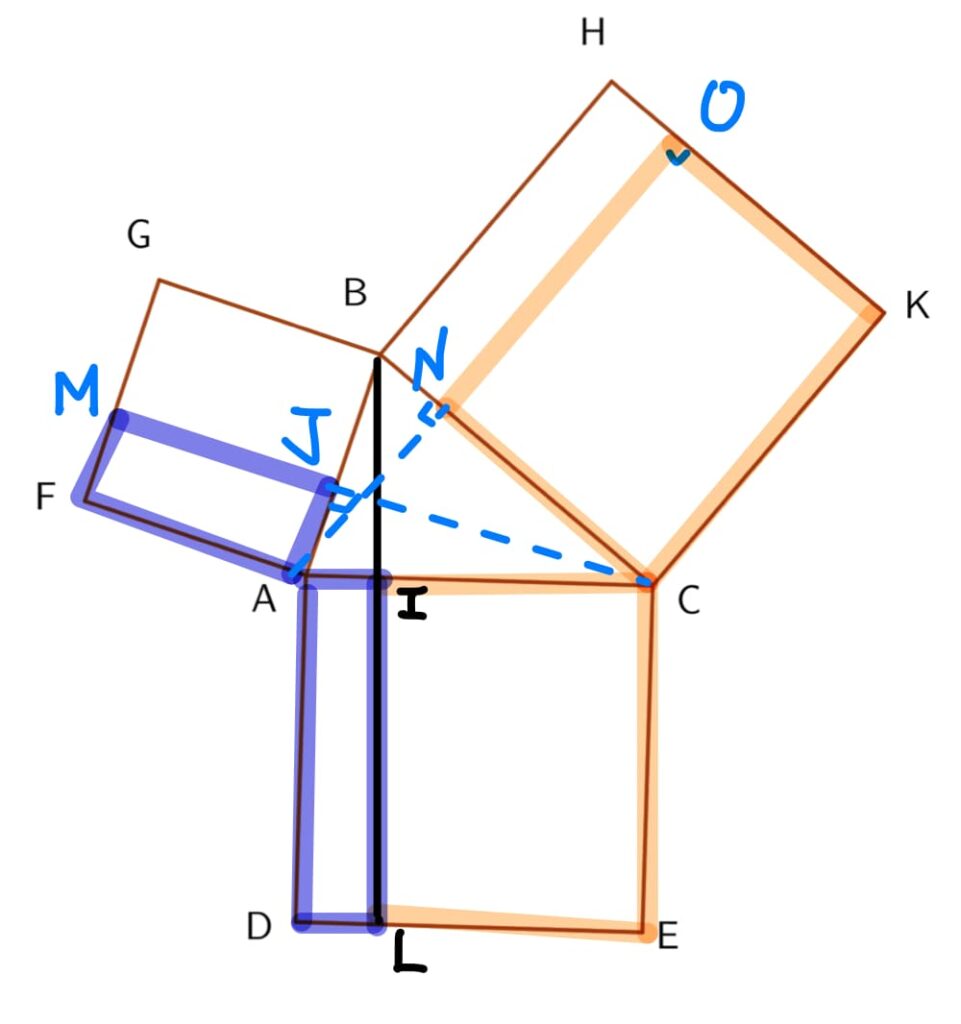
從這裡可以看出，修正項就是指矩形$BJMG$及矩形$BNOH$的面積，其中

$$矩形BJMG=\overline{BG}\times\overline{BJ}=c\times acosB (如下圖，在\Delta BCJ中，\overline{BJ}=acosB)$$ $$矩形BNOH=\overline{BH}\times\overline{BN}=a\times ccosB (如下圖，在\Delta ABN中，\overline{BN}=ccosB)$$

$$\begin{aligned} \overline{AC}^2=正方形ADEC的面積 &= 矩形ADLI的面積+矩形ILEC的面積 \\ &= 矩形AFMJ的面積+矩形CNOK的面積 \\ &= (正方形ABGF的面積-矩形BJMG的面積)\\ &+ (正方形BCKH的面積-矩形BNOH的面積)\\ &= (\overline{AB}^2-\overline{BC}\times\overline{AB}\times ccosB) + (\overline{BC}^2-\overline{BC}\times\overline{AB}\times cosB) \\ &=\overline{AB}^2+\overline{BC}^2 -2\overline{BC}\times \overline{AB}\times cosB \end{aligned}$$ 證畢。

餘弦定理我已經教了數十次，第一次看到這個證明，覺得很新鮮也很有趣。教科書的編排，往往是以學生容易學習與理解為主，不一定按照歷史脈絡與呈現當初數學家的原始思想，因此我時常鼓勵學生多閱讀課外書籍，不僅是為了考試，而是學習到知識的本質與內涵。

然而，在繁重的課業之下，大多數學生很難有時間閱讀整本書籍，因此採用單篇文章的形式，盡量以淺顯白話的方式書寫，方便學生們閱讀。

---

歡迎訂閱 高中數學數位學習電子報

---