歡迎訂閱，高中數學數位學習電子報

---

前言

我們於高一第1冊的課程中，已介紹了「正弦定理」及「餘弦定理」。顧名思義，正餘弦定理就是分別以正餘弦值來呈現三角形的邊角關係。這一篇文章，將進一步探討，正弦定理、餘弦定理及課本沒有介紹的「投影定理」三者的關係。事實上，它們本質上是一樣的。

接著，再引入複數平面的觀點，給出餘弦定理的另一個證明方式。

正弦定理

若 \(a、b、c\) 分別表示\(\Delta ABC\) 三內角 \(\angle{A}, \angle{B}, \angle{C}\) 的對邊長，且\(R\) 為其外接圓半徑。則 $$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$$

這個定理的證明在課堂上已介紹過，在此就不再贅述。

由正弦定理可知，$$sinA=\frac{a}{2R},\ sinB=\frac{b}{2R},\ sinC=\frac{c}{2R}$$

因此，\(a:b:c=sinA:sinB:sinC\)

投影定理(第一餘弦定理)

108課綱已刪除了投影定理，這就很像拼圖少了一角，我們再將它找回來。

投影定理的道理很簡單，我們分兩個情況來看。

如果 \(\angle{C}\) 是銳角，如下圖所示：

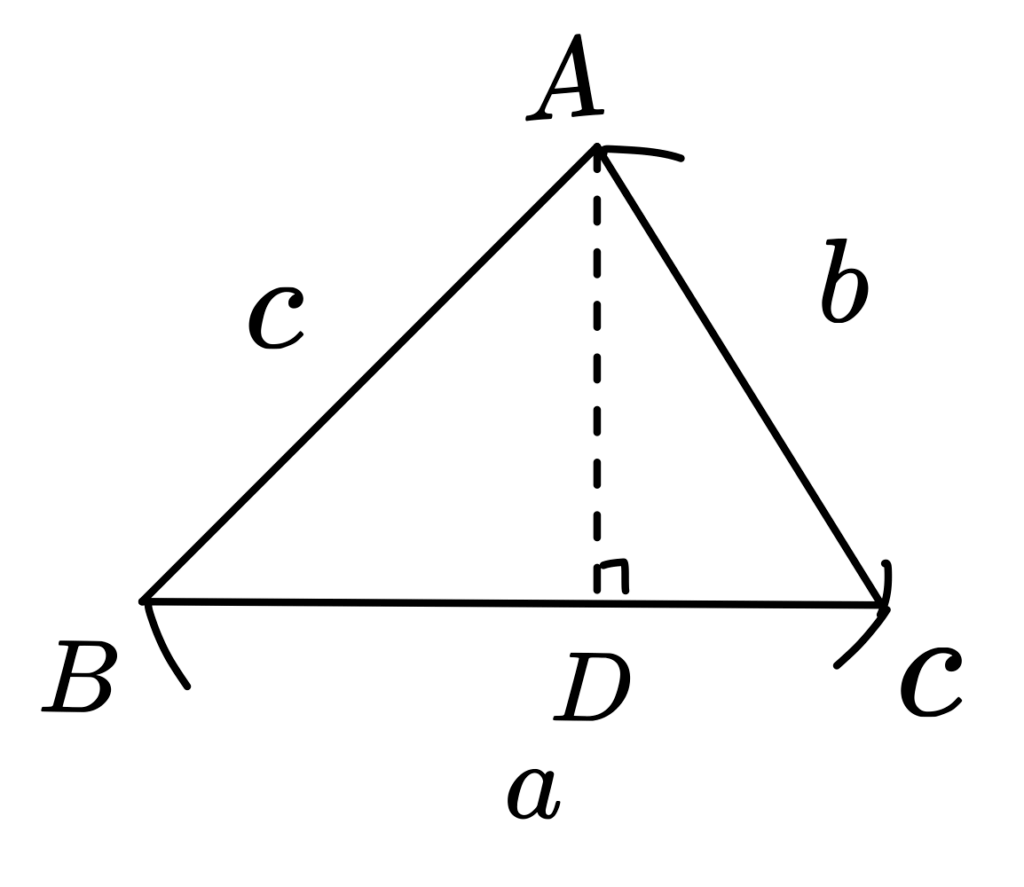
顯然 $$\overline{BC}=\overline{BD}+\overline{CD}$$ 即 $$a=ccosB+bcosC$$

如果 \(\angle{C}\) 為鈍角，如下圖所示

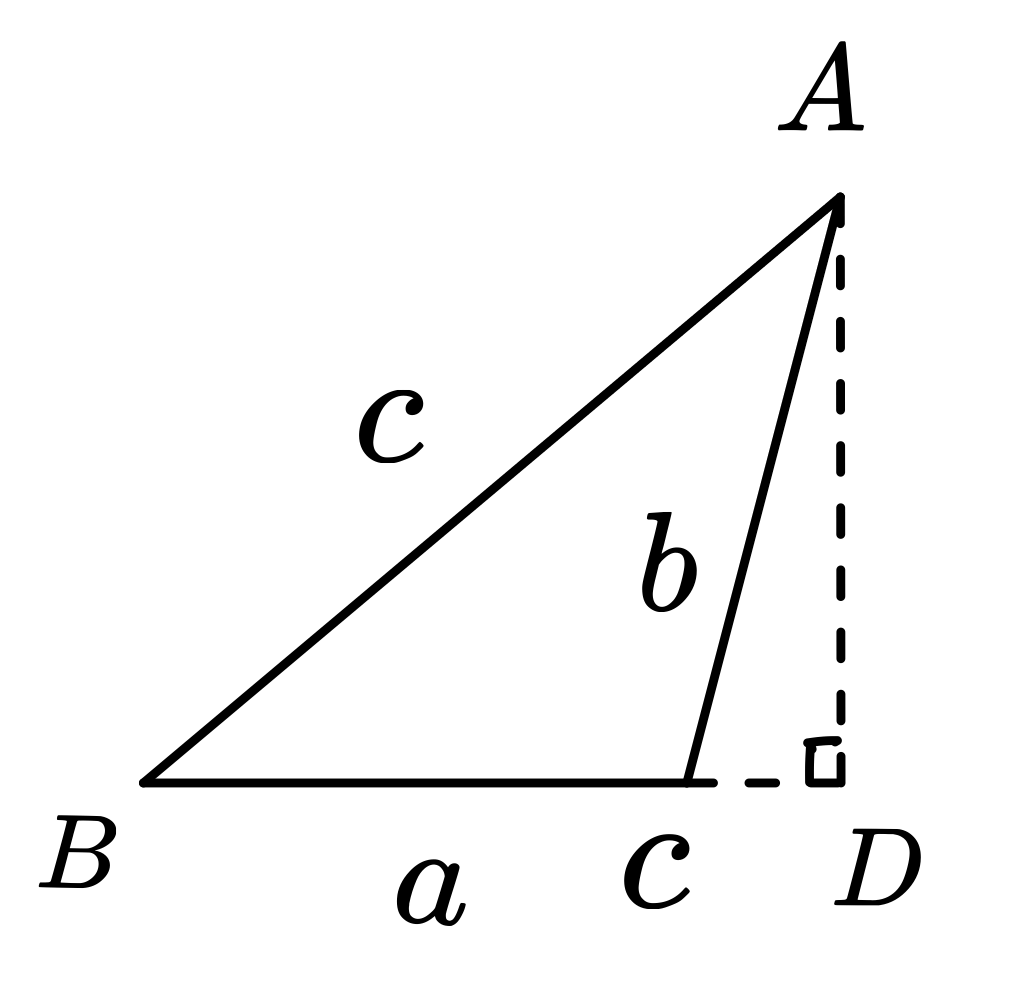
此時，$$\overline{BC}=\overline{BD}-\overline{CD}$$
即$$\begin{aligned}
a &= ccosB-bcos(\pi-\angle{ACB}) \\
&= ccosB+bcos\angle{ACB} \\
&= ccosB+bcosC
\end{aligned}$$

同理可得
$$\begin{aligned}
b &= acosC+ccosA \\
c &= acosB+bcosA
\end{aligned}$$

接著解聯立

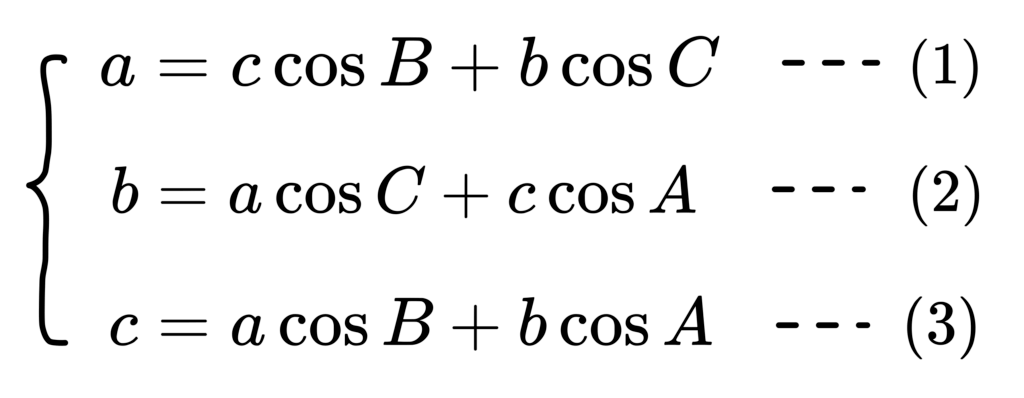
解 \(cosA、cosB、cosC\)

\((2)\times b + (3)\times c\)：
$$ b^2+c^2=a(bcosC+ccosB)+2bccosA = a^2+2bccosA$$ 移項整理可得
$$cosA = \frac{b^2+c^2-a^2}{2bc}$$ 同理可得
$$\begin{aligned}
cosB=\frac{a^2+c^2-b^2}{2ac} \\
cosC=\frac{a^2+b^2-c^2}{2ab}
\end{aligned}$$

這就是我們所熟知的餘弦定理，與課本切入的方式不同，提供給同學們參考。

由投影定理證明出餘弦定理之後，接著我們由餘弦定理證明正弦定理：

$$\frac{a^2}{sin^2A}=\frac{a^2}{1-cos^2A}$$

由餘弦定理可知，
$$\begin{aligned}
\frac{a^2}{1-cos^2A} &= \frac{a^2}{(1+cosA)(1-cosA)} \\
&= \frac{a^2}{(1+\frac{b^2+c^2-a^2}{2bc})(1-\frac{b^2+c^2-a^2}{2bc})} \\
&= \frac{a^2}{\frac{(b+c)^2-a^2}{2bc}\times\frac{a^2-(b-c)^2}{2bc}}\\
&= \frac{(2abc)^2}{(a+b+c)(b+c-a)(a+b-c)(a-b+c)}
\end{aligned}$$

由以上式子的對稱性可知，
$$\frac{a^2}{1-cos^2A}=\frac{b^2}{1-cos^2B}=\frac{c^2}{1-cos^2C}$$
因此正弦定理得證。

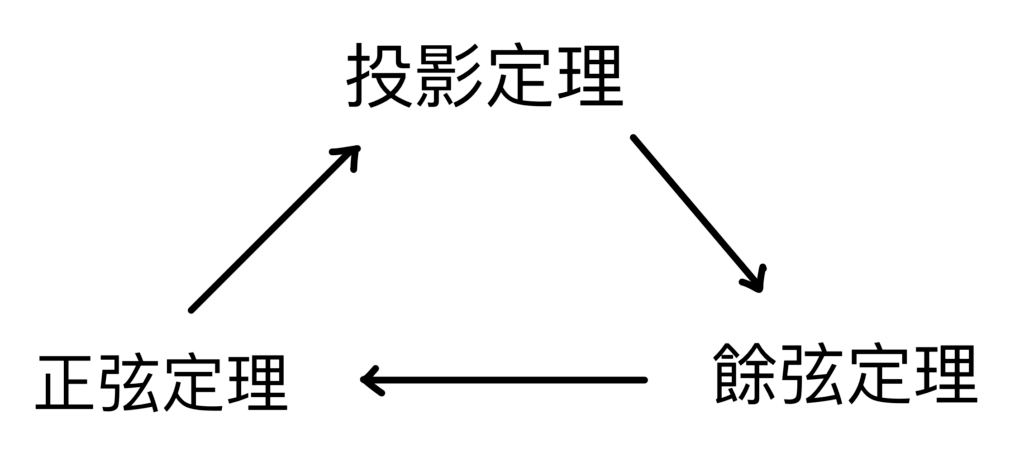
接著，只要能以正弦定理證明投影定理，那麼就可以說明「投影定理」、「正弦定理」、「餘弦定理」三者為等價關係。

由正弦定理可知，$$a=2RsinA, b=2RsinB, c=2RsinC$$

則
$$\begin{aligned}
ccosB+bcosC &= 2RsinCcosB+2RsinBcosC \\
&= 2Rsin(B+C) \\
&= 2Rsin(\pi-A) \\
&= 2RsinA = a
\end{aligned}$$

同理 $$bcosA+acosB =c , acosC+ccosA = b$$ 因此投影定理得證。

以上證明的順序如下圖所示：

餘弦定理的複數證法

來總結一下到目前為止，我們所知餘弦定理的證明方式：
方法一：坐標幾何證法 (課本提供)
方法二：直接使用畢氏定理
方法三：歐幾里德的風車證法
方法四：使用投影定理(第一餘弦定理)

接下來介紹第五個方法：複數證法

已知任何一個複數，都可以對應到坐標平面上的一個位置。

為了方便討論，不妨假設 \(\Delta ABC\) 的其中一個頂點 \(C\) 為原點。
那麼另外兩點 \(A\)、\(B\) 分別對應到複數 \(z_1\)、\(z_2\) 來表示，其中
$$z_1=b(cos\theta_1+isin\theta_1), z_2=a(cos\theta_2+isin\theta_2) $$

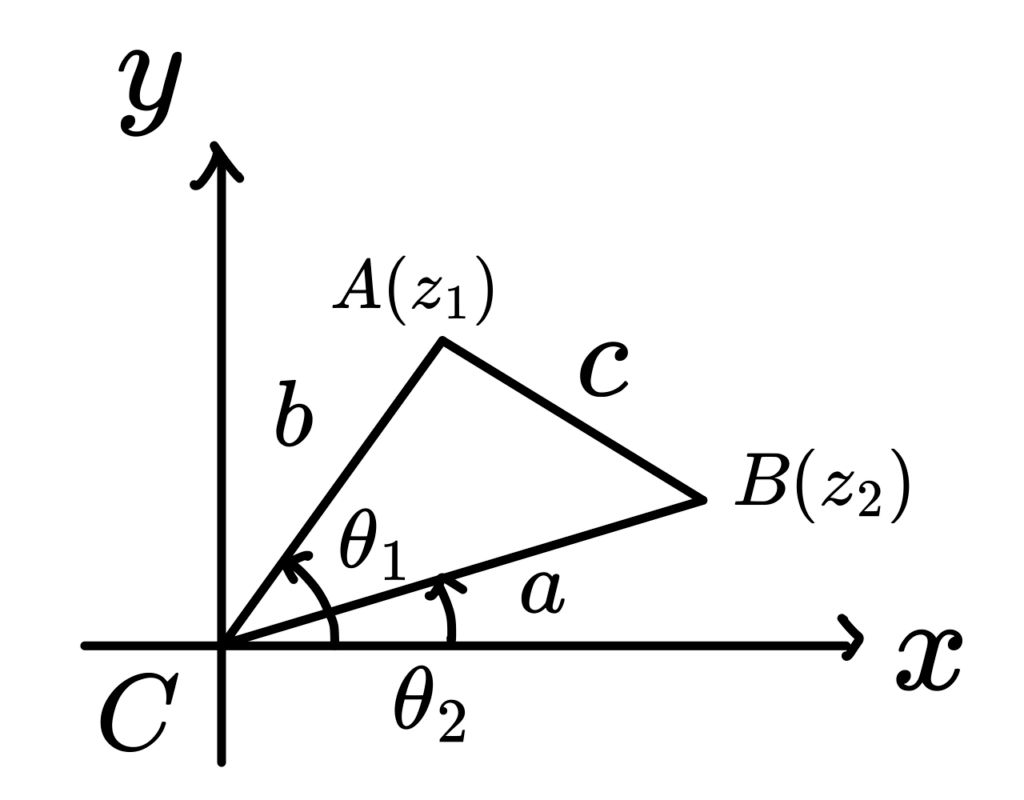
如上圖，
$$\begin{aligned}
c^2 &= |z_1-z_2|^2 \\
&=(z_1-z_2)(\overline{z_1}-\overline{z_2}) \\
&=|z_1|^2+|z_2|^2-z_1\overline{z_2}-z_2\overline{z_1}\\
&=|z_1|^2+|z_2|^2-2Re(z_1\overline{z_2})
\end{aligned} \tag{4}$$

其中要留意的是，$$z_1\overline{z_2}=ab(cos({\theta_1-\theta_2)}+isin{(\theta_1-\theta_2}))$$

因此 $$2Re(z_1\overline{z_2})=2abcos(\theta_1-\theta_2)=2abcosC \tag{5}$$

由式子(4)、(5)可得
$$c^2=a^2+b^2-2abcosC$$ 得證

在課堂上真的很難有機會對餘弦定理做這麼多的討論，其實我們學的很多公式或定理，
只是形式不同，但本質卻是一樣的。

這就像，剛開始出發時的起點與最終抵達的終點一致，只是過程中，
繞不同的路，所以沿路會看到不同的風景。

學習數學的過程中，多做題目固然重要，但是決定能力的高低，
往往在於思考是否深入。所以，與其做了一大堆題目但卻淺嚐輒止，
倒不如做幾道好題目，靜下心反覆思考，試著從不同的方式切入，
一題多解，相信對於數學成熟度的提升會更有幫助。