數學，是一門精確的學科。在學習數學的過程中，粗心錯誤常常造成學生不少的困擾。
這些看似無害的小錯誤，卻可能耗費大量時間卻仍導致答案出現偏差，進而影響考試成績與學習信心。
在這篇文章中，我將分享一些我多年來在教學和學習中累積的經驗，幫助同學降低在數學學習中粗心錯誤的頻率。

一、注意題目細節

首先，要仔細讀題，確保對題目的要求和限制有充分的理解。這包括理解問題在問什麼、需要我們求解什麼，
以及是否有附加條件。這些信息能夠幫助我們選擇適當的策略，從而避免走入錯誤的方向。

其次，請特別留意數字、符號和單位等細節。一個錯誤的數字或符號，就會導致整個計算過程功虧一潰。
例如，在代數運算中，替換數字，或者在單位換算中混淆不同的單位，去括號時變號，這些都是常見的錯誤。

此外，注意題目中的隱含條件也是至關重要的。有時題目並不會明確列出所有條件，而是間接地提供了一些資訊。
我們需要能夠捕捉這些隱含的條件，這有賴於我們學習過程中觀念的建立是否紮實，以及是否能夠抽絲剝繭，逐步推出關鍵條件。

例如：

我們知道 \(X\) 與 \(Y\) 的迴歸直線不表示此兩變數的關係式。如果對於迴歸直線的認識只停留在表面的形式，
是無法做出準確的判斷。此時就會有同學很牽強地選出答案，如果有錯還好，可以即時發現並修正，
萬一不小心猜對了可能連修正的機會也沒有了。這也就是為什麼有些學生寫了一堆題目但數學學不好的原因了。

這一題必須再進一步了解，迴歸直線的兩個重點：

1. 迴歸直線必過兩變數 \(X\) 與 \(Y\) 的算術平均數

2. 迴歸直線的斜率 $$m=r\cdot\frac{\sigma_y}{\sigma_x}$$ 依據題目給出的數據，推出 \(r=1\)，因此數據 \(X\) 與 \(Y\) 會完全落在迴歸直線上，
換句話說，\(X\) 與 \(Y\) 的關係式為 $$y=\frac{7}{8}x+5$$ 接著這題的判斷就容易許多。最後答案為 (C)，你寫對了嗎？

我們再來看一道國中的問題

算式左側是學生原本的算式，他答案選(C)，因為過程中只看到 \(21\times 6\)，卻忽略了其他分解方式。

為了讓問題更容易觀察，我們應該以符號取代數字，才能精確呈現出分解方式，如算式右側所示。
這是在解題中，我們必須去做轉換的部份，才可以避免太多情況而無法確定正確答案為何。

二、建立良好的解題習慣

養成良好的解題習慣，對於降低錯誤頻率至關重要。然而什麼是良好的解題習慣呢？
以下是一些我多年來在教學和學習中摸索出的心得，希望能夠對大家建立良好的解題習慣有所幫助。

首先，當遇到一道新的數學問題時，不要急於求解。建議先花些時間讀題，理解題目的要求和條件。
將題目中給定的資訊、限制和所求結果以表格或圖示清晰地列出，這有助於我們更好地掌握問題的全貌。
舉例來說

這個題目一般學生看了就暈了，此時不妨畫個表格呈現：

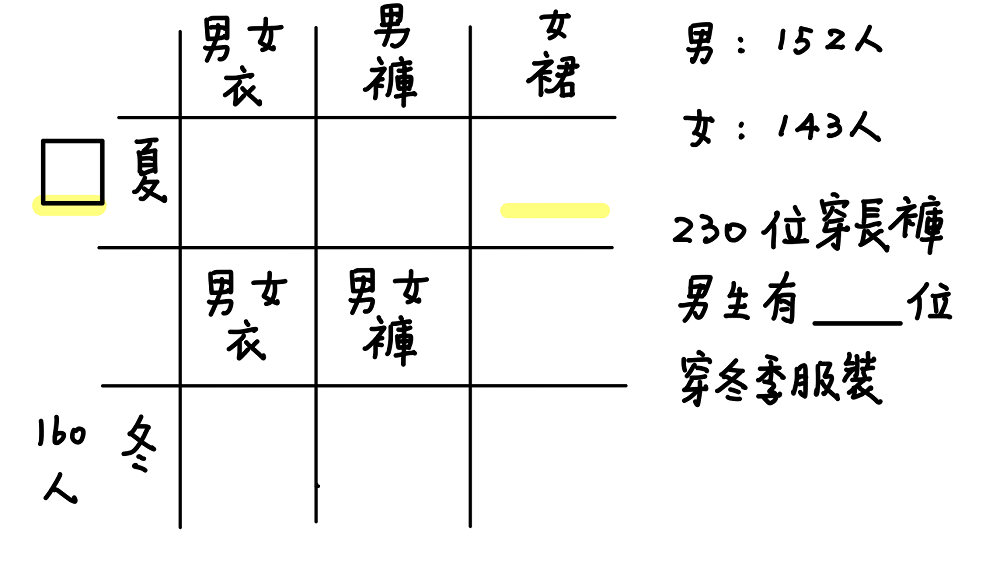
接著再經由推理依序將表格中的空格填入，解出此題。最後答案為82，你算對了嗎？

三、整理筆記與計算過程

接著，我們來談談整理筆記對於數學學習的重要性。

筆記是將思緒整理出來的工具，有助於建構觀念，捕捉細節、追蹤解題的邏輯。你可以通過回顧筆記，
發現可能的錯誤或疏漏。有時，解題過程可能變得複雜，容易迷失在細節中。有了清楚的筆記，
你可以隨時回顧和校對，確保解題的方向正確。

另一方面，計算過程的整理同樣至關重要。將每一步的計算清楚地呈現出來，確保數字和符號的運用正確無誤。當你進行複雜的計算時，
可能會在中途出現細微的錯誤，這些錯誤可能會影響最終答案的正確性。通過整理計算過程，你可以更容易地發現這些錯誤，及時進行修正。

總之，整理筆記並確實寫下計算過程是確保解題精確性的關鍵一步。它不僅可以幫助你更有條理地解決問題，還可以幫助你追蹤解題的邏輯，避免粗心錯誤。
無論是在學業還是日常生活中，建立這一良好習慣都將對你帶來巨大的益處。記住，整理筆記和計算過程，可以讓你的解題思路更加清晰，降低失誤的頻率。

四、交叉檢查與反思

在解決數學問題的過程中，交叉檢查是確保答案準確性的關鍵步驟，有助於找出潛在的錯誤。

當我們在解題過程中投入大量時間和精力後，可能會因為疲勞或專注力下降而遺漏某些細節。這時，進行交叉檢查就至關重要。
交叉檢查的重點是將不同的解題方法應用於同一問題，或者反向驗證答案的合理性。這種方法可以幫助我們意識到可能的錯誤，
將解答過程與不同的角度對比，找出其中的不一致之處。

以下這道題目的算式學生已經修正過，錯誤的原因是忽略了題目關鍵條件：\(a\) 為正整數，將答案寫 \(0\)。

五、反覆練習

建立了正確觀念後，必須通過反覆的練習，才能真正鞏固所學。

反覆練習可以強化神經通路，不僅能夠幫助我們提高解題的速度和準確度，還能夠減少犯錯的機會，從而在考試中取得好的成績。

其次，反覆練習能夠幫助我們深化對數學概念的理解。透過反覆的操作和應用，我們能夠從不同的角度理解一個概念，從而建立起更全面和深入的知識體系。
這種深刻的理解使我們能夠在面對更複雜的問題時，更靈活地運用所學知識。

另外，反覆練習還能夠幫助我們發現並改進自己的薄弱環節。透過不斷地解題和練習，我們可以識別出我們在哪些方面容易出錯，
然後有針對性地進行強化學習。這種持續的修正和改進過程，能夠讓我們不斷進步，提高解題的準確性和效率。

最後，反覆練習在應對考試壓力中扮演著重要角色。透過多次練習，我們能夠建立自信，熟悉考試的題型和範圍。
這種自信可以幫助我們在考試中保持冷靜，減少因緊張而導致的粗心錯誤。

六、放鬆與專注：實現數學學習的最佳狀態

在數學學習的過程中，放鬆與專注是兩個看似矛盾但卻密切相關的要素。
這兩者的結合，能夠幫助我們進入最佳的學習狀態，提高解題的效率和準確性，同時減少粗心錯誤的發生。

首先，讓我們談談放鬆的重要性。放鬆不僅有助於釋放壓力，還能夠緩解焦慮和緊張感，讓我們更好地應對數學學習中的挑戰。
當我們處於放鬆的狀態時，大腦更容易保持清楚，思緒更易流暢，這對於解題是非常有利的。放鬆還可以幫助我們保持積極的學習態度，
不會因困難而灰心喪志，從而能夠堅持下去，克服困難。

然而，單純的放鬆可能會使我們陷入過於懈怠的狀態，這時專注就變得尤其重要。專注意味著全神貫注地投入到解題過程中，
忽略干擾，專心解決問題。在解題時，保持專注能夠幫助我們更好地理解問題，避免遺漏重要細節，從而減少粗心錯誤的可能性。
專注也能夠幫助我們更快地找到解題思路，更有效地應用所學知識。

在實際操作中，如何在放鬆與專注之間找到平衡是一個值得思考的問題。一種方法是在學習過程中適時地進行休息，放鬆身心，避免過度疲勞。
在解題時，可以通過深呼吸和冥想等方式，幫助自己保持冷靜和專注。同時，培養對數學學習的興趣和熱情，也能夠讓我們更自然地進入放鬆和專注的狀態。

總之，放鬆與專注是實現數學學習成功的關鍵。通過在學習過程中合理運用這兩種要素，我們能夠進入最佳的學習狀態，提高解題效率和準確性。
在面對數學的挑戰時，保持平衡的放鬆和專注，將成為我們克服困難，走向成功的堅實支撐。

結語：成為精確的數學高手，鑄就不凡的數學之路

在數學的世界裡，精確無誤是我們始終追求的目標。透過一系列細緻的方法和有效的策略，我們可以成為精確的數學高手，為自己鑄造一條充滿意義和成就的不凡之路。

從「注意題目細節」開始，我們學會了從每一個問題中擷取關鍵資訊，了解問題的要求和限制，這是解題的基石。接著，在「建立良好的解題習慣」中，我們通過整理筆記、練習計算過程等方法，確保解題的有條不紊，減少粗心錯誤。我們也了解到「交叉檢查與反思」的重要性，通過從不同角度檢視解答，發現潛在錯誤，同時深化對解題過程的理解。

「反覆練習」是鞏固技能的不二法門。通過持續的練習，我們不僅提高了解題的速度和準確度，更深化了對數學概唸的理解。這種持之以恆的努力，讓我們在面對考試和實際問題時，能夠自信地掌握數學的精髓。

最後，我們學會了「放鬆與專注」的平衡。通過適時的休息和冥想，我們保持冷靜和專注，進入最佳的學習狀態。這種平衡使我們能夠更好地應對數學學習的挑戰，減少粗心錯誤的可能性。

成為精確的數學高手不僅是我們的目標，更是一個持續的過程。這需要我們的耐心、努力和不斷的學習。透過運用這些關鍵策略，我們將能夠在數學的海洋中航行自如，攀登數學的高峰。讓我們共同努力，成為精確、自信的數學高手，為未來的學習和挑戰做好充分的準備。在這個充滿精彩的數學之旅中，讓我們一起追求卓越，創造卓越！