八年級上學期，學生要進入到根號的世界。
也就是對於數字的概念，將由有理數擴張至無理數。
介紹完根號後，緊接著，畢氏定理登場。
畢氏定理，又稱為「畢達哥拉斯定理」、「勾股定理」、「商高定理」，
是在描述直角三角形三邊長的關係：兩股平方和＝斜邊長的平方。
如下圖所示，假設此直角三角形的兩股長分別為 \(x\) 與 \(y\)，斜邊長為 \(z\)，則$$x^2+y^2=z^2$$
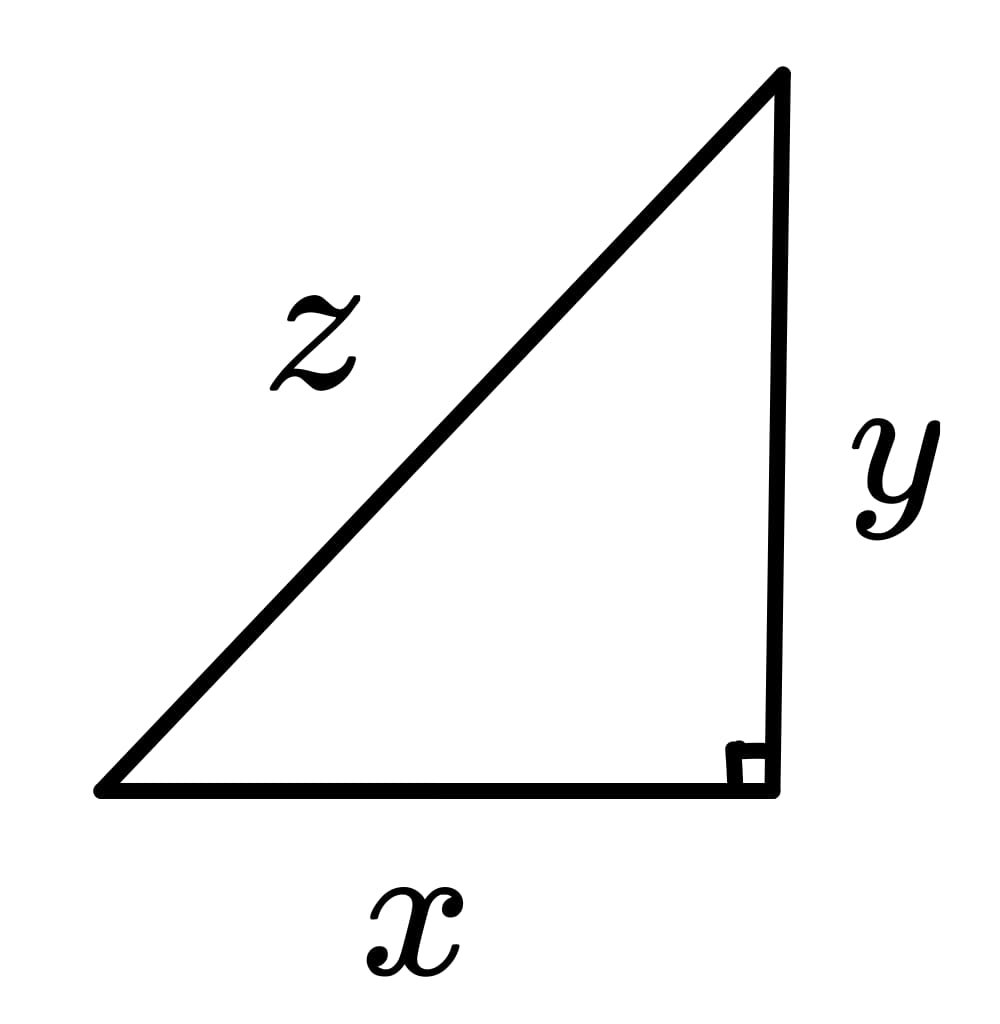
這個定理清晰易懂，神奇的是，文獻記載，竟然有三百多種證明方式。
不急著證明，先想想，有哪些直角三角形，其三邊長為正整數呢？
最常見的有：(3，4，5)；(5，12，13)；(7，24，25)；(8，15，17)；(9，40，41)、…還有很多。
此稱為畢氏數。
但是有一些成比例的就先不考慮了，例如：(6，8，10)；(9，12，15)；(10，24，26)、…這類的。
以倍數產生的畢氏數很無聊對吧！
因此，我們要專注在三數互質的畢氏數。也就是說，\((x,y,z)=1\) 且滿足 $$x^2+y^2=z^2$$
我們將這樣的畢氏數稱為原始的畢氏數(Primitive Pythagorean triples)。
但是優秀的你一定不滿足於此，必定想知道到底有沒有一個原始畢氏數的通解？
然後我們可以用這個通解找到千千萬萬的原始畢氏數！
跟你說答案之前，我們先來觀察一下，對於原始的畢氏數 \(x,y,z\) 滿足$$x^2+y^2=z^2$$ \(x\)、\(y\) 必定一個為奇數、另一個為偶數對吧！
為什麼呢？不妨簡單論證一下：如果 \(x,y\) 皆為偶數，則 \(z\) 必定為偶數，因此 \(x,y,z\) 不可能互質。
如果 \(x,y\) 皆為奇數，那麼 \(z\) 必定是偶數。這會造成 \(x^2+y^2\) 被 \(4\) 除餘 \(2\)，\(z^2\) 被 \(4\) 整除。
以同餘的符號來寫會更清楚 $$x^2+y^2 \equiv 2 \ mod \ 4, z^2 \equiv 0 \ mod \ 4$$
因此造成矛盾。
既然如此，不失一般性，可以假設 \(y\) 為偶數。
直接公佈答案：此原始畢氏數的通解可表示為
$$\begin{aligned}
x &= m^2-n^2 \\
y &= 2mn \\
z &= m^2+n^2
\end{aligned}$$其中 \(m, n\) 為正整數，且 \(m>n\)，\((m,n)=1\)，且必定為一奇一偶。
證明這個通解之前，先帶幾組數字試試：
(a) \(m=2\)、\(n=1\)：\((x,y,z)=(3,4,5)\)
(b) \(m=3\)、\(n=2\)：\((x,y,z)=(5,12,13)\)
來點不一樣的吧：
(c) \(m=57\)、\(n=34\)：\((x,y,z)=(2093,3876,4405)\)
我保證你一定從來沒看過這組畢氏數。
是不是有慢慢感受到數學的威力了呢？
接著進行這篇文章的重點：這個通解是怎麼寫出來的？
我們朝兩個方向論證：
首先，如果有一組正整數 \(x,y,z\) 滿足 $$x^2+y^2=z^2, \ (x,y,z)=1 \tag{1}$$ 其中 \(y\) 是偶數、\(x, z\) 是奇數。
那麼很容易看出來 \((x,y)=(y,z)=(z,x)=1\)。(如果你看不出來，可以用反證法試試)
可以將第 (1) 式移項一下：$$y^2=z^2-x^2=(z+x)(z-x)$$ 等號兩邊同除以 \(4\) 可得：$$(\frac{y}{2})^2 = (\frac{z+x}{2})\times (\frac{z-x}{2}) \tag{2}$$
要留意，\(\frac{z+x}{2}\) 與 \(\frac{z-x}{2}\) 兩數互質。為什麼？
同學可以自己練習證明看看，再繼續往下閱讀。
公佈答案，令 \(\frac{z+x}{2}\) 與 \(\frac{z-x}{2}\) 的最大公因數為 \(d\)，
那麼 $$d \mid \frac{z+x}{2}, \ d \mid \frac{z-x}{2}$$ 故 $$d \mid \frac{z+x}{2}+\frac{z-x}{2} \ 且 \ \ d \mid \frac{z+x}{2} – \frac{z-x}{2}$$ 整理可得 $$d \mid z \ \ 且 d \mid x$$ 因為 \(x, z\) 互質，所以 \(d=1\)
既然如此，重回第 (2) 式可看出，\(\frac{z+x}{2}\) 及 \(\frac{z-x}{2}\) 是完全平方數！
也就是說，存在兩個正整數 \(m, n\) 滿足 $$\frac{z+x}{2}=m^2, \ \frac{z-x}{2}=n^2$$
因此 \(m>n>0, (m,n)=1\) $$m^2-n^2=x,\ 2mn=y, \ m^2+n^2=z$$
前面已經證明過 \(m, n\) 兩數互質，所以此兩數必定1偶1奇或2奇。
如果 \(m, n\) 皆為奇數，則 \(x, y, z\) 皆為偶數，此與上述 \(x, z\) 互質矛盾。
所以沒有其他選擇了，\(m, n\) 必定為1奇1偶。
至此，我們已經證明了畢氏數的通解必定呈現出來的形式。
還沒結束
另一方面，如果給定了兩個正整數 \(m, n\)，令 $$x=m^2-n^2, \ y=2mn, \ z=m^2+n^2$$ 且 \(m, n\) 為 \(1\) 奇 \(1\) 偶且互質的兩數。 那麼要驗證 \((x,y,z)\) 是原始的畢氏數。我們分兩步驟進行：
步驟1：\((x,y,z)\) 是畢氏數
$$\begin{aligned}
x^2+y^2 &= (m^2-n^2)^2+(2mn)^2 \\
&= m^4-2m^2n^2+n^4+4m^2n^2 \\
&= m^4+2m^2n^2+n^4 = (m^2+n^2)^2 = z^2
\end{aligned}$$
步驟2：\((x,y,z)=1\)
令 \((x,y,z)=d\)，則 $$d\mid m^2-n^2\ , d \mid 2mn\ , d \mid m^2+n^2$$
因為 \(m, n\) 為 \(1\) 奇 \(1\) 偶，所以 \(x, z\) 皆為奇數。
那麼，\(d\) 必定是一個奇數。
我們來排除 \(d>1\) 的情況：
對於任何大於 \(1\) 的奇數 \(d\)，存在一個奇質數 \(p\) 將其整除。
用符號表示就是 \(p \mid d\)，因此 \(p \mid x\)、\(p \mid z\) 進而可知 \(p | z+x\)、\(p | z-x\)
因為 \(z+x=2m^2\) 且 \(z-x=2n^2\)，所以 \(p\mid 2m^2, \ p\mid 2n^2\)。
既然 \(p\) 是奇數，那麼 \(p \mid m^2\) 且 \(p \mid n^2\)，
此將導致 \(p \mid m\) 且 \(p \mid n\)，也就是 \(m, n\) 兩數不互質，造成矛盾。
因此 \(d=1\)
看到這裡，希望你的腦袋還沒打結…。
畢氏定理還有很多故事可以說，但為了讓同學好吸收，
這篇文章就先寫到這邊，我們下篇文章見囉！
如果文章有繆誤，歡迎私訊告訴我，感謝！
免費訂閱 數學數位學習電子報
訂閱電子報，加入數學科普書籍閱讀計畫
No comments! Be the first commenter?