台大電資申請入學 二階筆試 第四講 三角函數

在學習三角函數這個單元時，以下四道類似題，提供了很好的練習機會：

第一題：在 $\Delta ABC$ 中，求

$$cosA + cosB + cosC \ 之最大值$$
第二題：在 $\Delta ABC$ 中，求 $$sinA + sinB + sinC \ 之最大值$$
第三題：銳角 $\Delta ABC$ 中，求 $$tanA + tanB + tanC \ 之最小值$$
第四題：銳角 $\Delta ABC$ 中，求 $$cotA + cotB + cotC \ 之最小值$$

因為每個三角函數的特性不同，因此每一題的解題策略也都不同。

是什麼樣的三角形，會使得三角函數的和發生極值呢？

有些學生做題之前，會先猜正三角形！答案也確實如此。

因此，作為一道練習題，這會是不錯的練習。但作為一道考題，
會比較適合出現在計算題，依過程計分。

首先，我們要先思考一件事，由於 $\angle{A}$、 $\angle{B}$、 $\angle{C}$ 是三角形的三個內角，
必定滿足

$$\angle{A}+\angle{B}+\angle{C}=\pi$$
這是這一題唯一的條件，接下來就是考驗我們對於三角恆等式及其圖形能否靈活運用了。

先來看第一題：首先利用和差化積公式，將 $cosA+cosB$ 合併，並且將$\angle{A}+\angle{B}$ 以 $\pi-\angle{C}$ 取代：

$$\begin{aligned} 原式 & = 2cos\frac{A+B}{2}cos\frac{A-B}{2}+cosC \\ & = 2cos\frac{\pi-C}{2}cos\frac{A-B}{2}+cosC \\ &\leq 2sin\frac{C}{2}+cosC \ \ \ (餘角關係) \\ &= 2sin\frac{C}{2}+1-2sin^2\frac{C}{2} \ \ \ (餘弦函數的二倍角公式) \\ &= -2(sin\frac{C}{2}-\frac{1}{2})^2+\frac{3}{2} \ \ \ (配方) \\ &\leq \frac{3}{2} \end{aligned}$$

使用不等式時，都要確認等號成立的條件。以這題來說，當

$$cos\frac{A-B}{2}=1 \ \ 以及 \ \ sin\frac{C}{2}=\frac{1}{2}\ \ 時，等號成立$$
即 $$\angle{A}=\angle{B}=\angle{C}=60^{\circ} \ 時，等號成立$$

以上方法用在第二題似乎行不通了，必須換個想法。利用正弦函數凹口向下的特性：

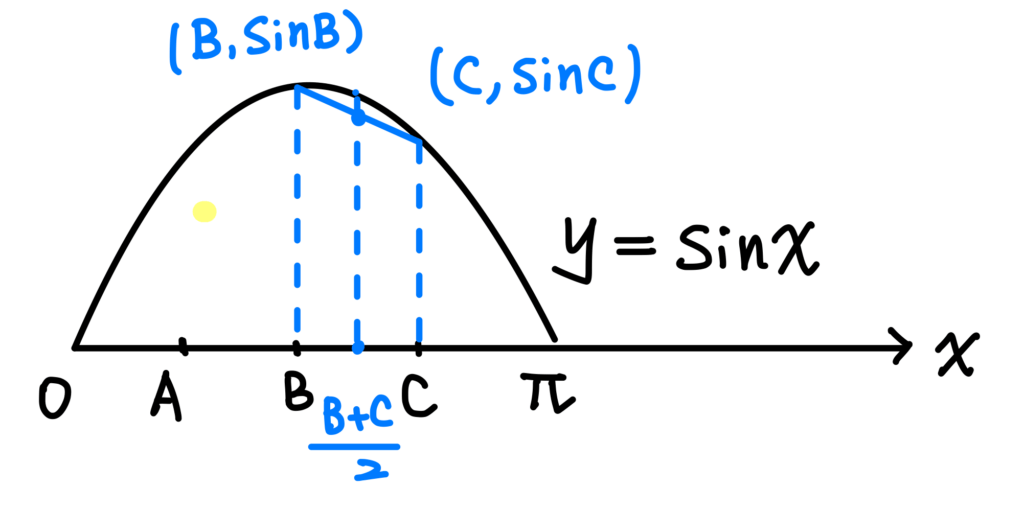
在線段 $\overline{BC}$ 上來看，線段上的點，其高度低於曲線上的點，因此可得

$$\frac{sinB+sinC}{2}\leq sin\frac{B+C}{2}\tag{1}$$

同樣道理，考慮點 $(A,sinA)$ 以及 點$(\frac{B+C}{2}, sin\frac{B+C}{2})$ 的連線段：

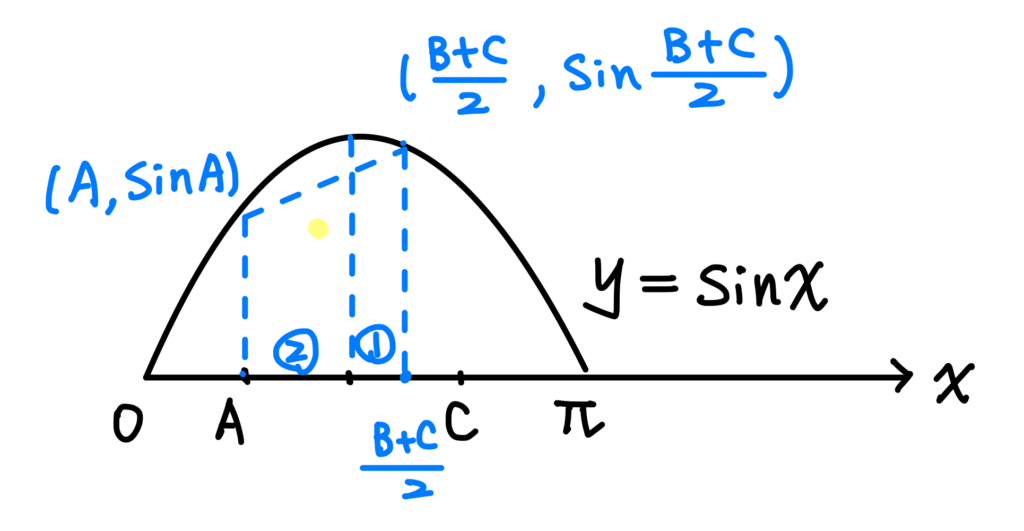
並且依比例 $2:1$ ，考慮 $x=\frac{A+B+C}{3}$ 在線段及正弦函數圖形上的點的 $y$ 坐標：

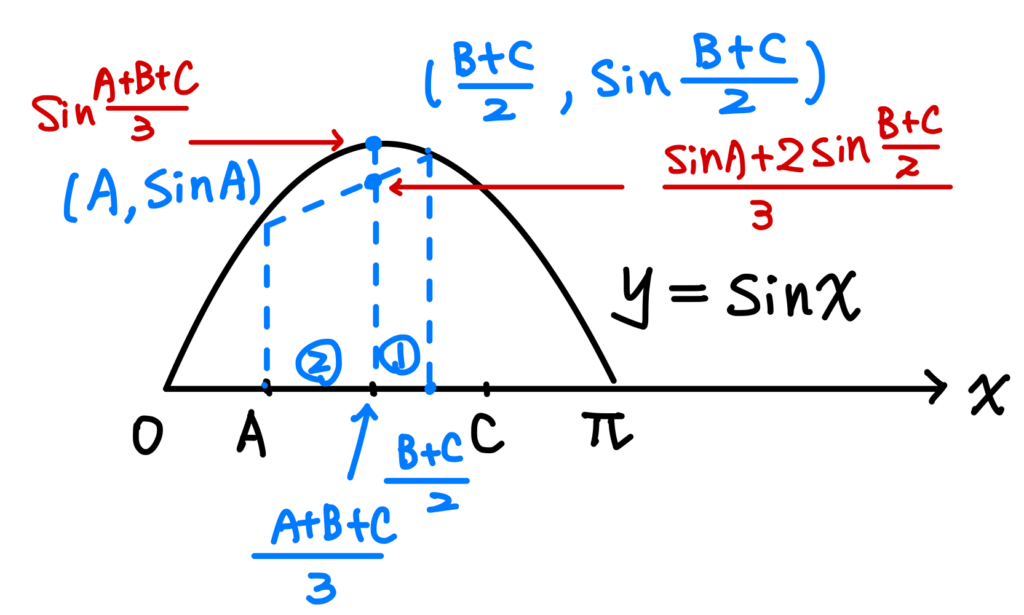
由於線段上的點，其高度不高於曲線上的點，因此

$$\frac{sinA+2sin\frac{B+C}{2}}{3}\leq sin\frac{A+B+C}{3} \tag{2}$$
再利用第 (1) 式可得 $$\frac{sinA+sinB+sinC}{3}\leq \frac{sinA+2sin\frac{B+c}{2}}{3}\tag{3}$$
合併第(2)式及第(3)式可得： $$\frac{sinA+sinB+sinC}{3}\leq sin\frac{A+B+C}{3}=sin\frac{\pi}{3}=\frac{\sqrt{3}}{2}$$
因此 $sinA+sinB+sinC$ 的最大值為 $\frac{3}{2}\sqrt{3}$

要留意以上過程中，等號成立的條件為

$$\angle{A}=\angle{B} = \angle{C} = \frac{\pi}{3}$$

第三題，關於在於以下恆等式

$$tanA+tanB+tanC=tanA\cdot tanB \cdot tanC$$ 推導方式只要用到正切函數的和角公式即可

$$\begin{aligned} tanC &= tan(\pi-(A+B)) \\ &= -tan(A+B) \\ &= -\frac{tanA+tanB}{1-tanAtanB} \end{aligned}$$ 等號兩邊同乘以 $1-tanAtanB$ 並且移項即可得出 $$tanA+tanB+tanC=tanA\cdot tanB \cdot tanC$$
為了方便計算，不妨先令 $tanA+tanB+tanC=x$

因為 $\Delta ABC$ 為銳角三角形，所以三個角度的正切值均為正數，直接應用算幾不等式：

$$\frac{tanA+tanB+tanC}{3} \geq \sqrt[3]{tanA\cdot tanB\cdot tanC}$$ 兩邊三次方可得 $$\frac{x^3}{27}\geq x$$
稍微解一下這個不等式：
$$\begin{aligned} \frac{x^3}{27}\geq x \Longleftrightarrow x^2-27 \geq 0 \Longleftrightarrow x\geq 3\sqrt{3} \end{aligned}$$

第四題，同樣地，我們要先推導出餘切函數的恆等式：

$$cotAcotB+cotBcotC+cotCcotA=1$$
$$\begin{aligned} cotC &= cot(\pi-(A+B)) \\ &= -cot(A+B) \\ &= -\frac{cotAcotB-1}{cotA+cotB} \end{aligned}$$ 移項整理可得 $$cotAcotC+cotBcotC+cotAcotB=1$$
推導過程中，要用到餘切函數的和角公式，課本沒有提到這部份，同學們可試著自己推導看看。

回到這一題，先考慮 $cotA+cotB+cotC$ 的平方，為什麼呢？

因為我們看到上述推導的恆等式中，出現了 $cotAcotB+cotBcotC+cotCcotA$ 這一項，
所以很自然地想到，三數之和的平方。

$$\begin{aligned} (cotA+cotB+cotC)^2 &= cot^2A+cot^2B+cot^2C +2cotAcotB + 2cotBcotC +2 cotCcotA \\ &= cot^2A+cot^2B+cot^2C +2 \end{aligned}$$
為了方便書寫，令 $cotA+cotB+cotC=x$，因此 $cot^2A+cot^2B+cot^2C=x^2-2$

接著，應用柯西不等式：

$$(cot^2A+cot^2B+cot^2C)(1^2+1^2+1^2)\geq (cotA+cotB+cotC)^2$$
$$(x^2-2)\cdot 3 \geq x^2 \Longleftrightarrow x^2 \geq 3 \Longleftrightarrow x\geq \sqrt{3}$$

總結：四個看起來差不多的問題，處理方法有相似之處，卻也截然不同。

正如英國數學家 James Joseph Sylvester(1814-1897) 說的：

數學關注在理解事物的「異中之同」與「同中之異」。

這篇文章就先分享到這邊，如果你對這樣的主題有興趣，歡迎訂閱高中數學數位學習電子報，
接收高中數學學習的相關資訊。

---