
免費訂閱 數學數位學習電子報
訂閱電子報,加入數學學習及科普書籍閱讀計畫
判斷一個題目的優劣有一個重要指標,就是這一道題目是否具備多個思考面向。
一個經典例子是,畢氏定理:文獻中記載,有三百多種證明方式。
從這些證明方法,可以體現出古人思考的智慧。
還有很多這樣的例子,
例如:算幾不等式的證明、平方級數和的公式推導、…。
另外,我發現有些版本的課本後面,也有一題多解專區,
演示一道題目如何用多種方法切入解題。容易被忽略,建議同學一定要閱讀。
這一篇文章,我要介紹一道最近給學生寫的小考題,
讓讀者也可以一同參與一題多解的趣味。
你只需要具備國中與高中數學的基本知識就可以理解。
問題:考慮一個平行四邊形 \(ABCD\),\(E\)、\(F\) 分別是 \(\overline{BC}\) 與 \(\overline{CD}\) 的中點,
求 \(\Delta AEF\) 與平行四邊形 \(ABCD\) 的面積之比值。(如下圖所示)
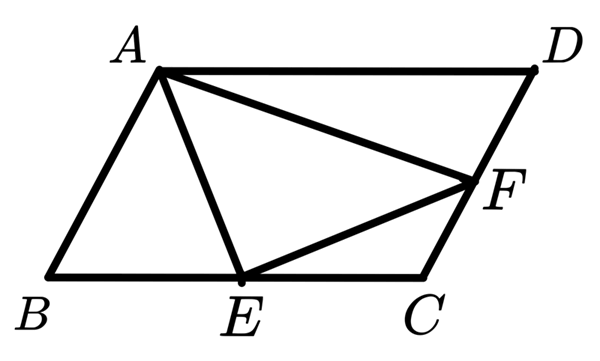
有很多方法可以處理,先從簡單的開始吧。
方法1:考慮一個特例
考慮此平行四邊形為長方形的情形,如下圖所示:
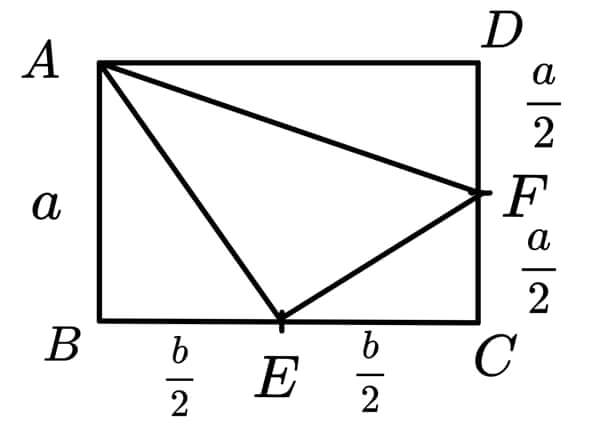
那麼,\(\Delta AEF 的面積 = 矩形ABCD的面積-\Delta ABE的面積 – \Delta CEF的面積 – \Delta ADF的面積 \),故
$$ \Delta AEF的面積 = ab – \frac{1}{2}\cdot a\cdot \frac{b}{2} – \frac{1}{2}\cdot \frac{a}{2}\cdot \frac{b}{2} – \frac{1}{2}\cdot b\cdot \frac{a}{2} = \frac{3}{8}\cdot ab
$$ 即 $$\frac{\Delta AEF的面積}{平行四邊形ABCD的面積}=\frac{3}{8}$$
這個方法很簡單,但是不夠嚴謹。
我們要如何說明對於任何一個平行四邊形,這個比值會是固定不變的呢?
這時候我們就必須有更一般的做法。
方法2:同樣用扣除的方式處理
因為題目只是問比值,所以不用真的將面積算出來。
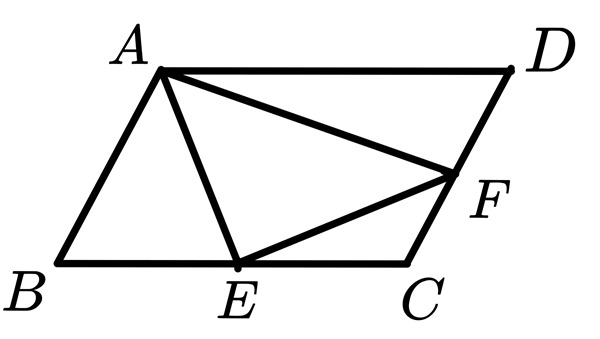
設平行四邊形 \(ABCD\) 的面積為 \(x\)
顯然,$$\Delta ABE\ 的面積 = \Delta ADF\ 的面積 = \frac{1}{4}x$$ $$\Delta CEF的面積=\frac{1}{8}x$$
因此,
$$\begin{aligned}
\Delta AEF 的面積 &= 平行四邊形 ABCD的面積-\Delta ABE 的面積 – \Delta CEF 的面積 – \Delta ADF 的面積 \\
&= x – \frac{x}{4} – \frac{x}{8} – \frac{x}{4}= \frac{3}{8}x
\end{aligned}$$
同樣可求出比值 \(\frac{3}{8}\)
方法3:使用三角函數
同方法2,但是使用三角函數表達
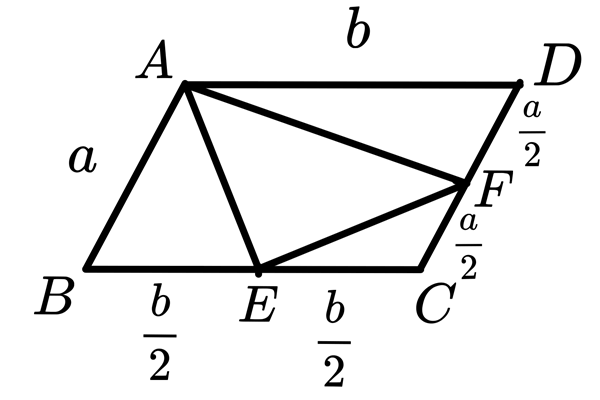
$$\begin{aligned}
\Delta AEF\ 的面積 &= 平行四邊形 ABCD的面積-\Delta ABE 的面積 – \Delta CEF 的面積 – \Delta ADF 的面積 \\
&= ab\cdot sinB – \frac{1}{2}a\cdot\frac{b}{2}\cdot sinB – \frac{1}{2}\cdot\frac{a}{2}\cdot\frac{b}{2}\cdot sinC – \frac{1}
{2}\cdot\frac{a}{2}\cdot b\cdot sinD \\
&= ab\cdot sinB – \frac{1}{4}absinB – \frac{1}{8}absinC – \frac{1}{4}absinD \\
&= (1-\frac{1}{4}-\frac{1}{8}-\frac{1}{4}) \cdot absinB \\
&= \frac{3}{8}\cdot 平行四邊形\ ABCD\ 的面積
\end{aligned}$$
其中要注意的是,\(sinC = sin(\pi-B)=sinB\),且 \(sinD = sin B\)
雖然寫法上比方法2複雜了一些,但卻是熟悉三角函數不錯的練習。
因為我對於高中數學的熟悉度高過於國中數學,
所以當時看到這一道題目時,第一時間想到的是這個方法。
方法4:拼接
到目前為止,我們都是用扣的,那能不能改用加的呢?
當然可以,看看下面這個圖:
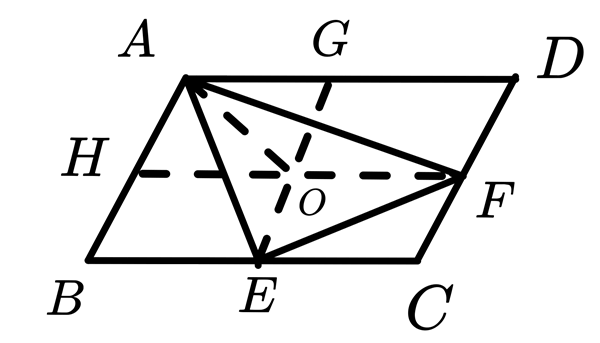
將兩組對邊的中點連接形成兩條線段 \(\overline{GE}\)、\(\overline{HF}\),設交點為 \(O\),
此兩線段可以將此平行四邊形的面積四等份。
接著連接 \(\overline{AO}\)。
此時
$$
\Delta AEF\ 的面積 = \Delta AOE\ 的面積 + \Delta AOF\ 的面積 + \Delta OEF\ 的面積 \tag{1}
$$ 其中
$$\begin{aligned}
\Delta AOE\ 的面積 = \frac{1}{2}\cdot 平行四邊形BHOE\ 的面積 = \frac{1}{8}\cdot 平行四邊形ABCD\ 的面積 \\
\Delta AOF\ 的面積 = \frac{1}{2}\cdot 平行四邊形DGOF\ 的面積 = \frac{1}{8}\cdot 平行四邊形ABCD\ 的面積 \\
\Delta EOF\ 的面積 = \frac{1}{2}\cdot 平行四邊形ECFO\ 的面積 = \frac{1}{8}\cdot 平行四邊形ABCD\ 的面積
\end{aligned}$$ 回到第 (1) 式可得 $$\Delta AEF\ 的面積=\frac{3}{8}\cdot 平行四邊形ABCD\ 的面積$$
這個方法直接易懂。
方法5:先加再扣
結合前面四種方法,也可以先加再扣。
如下圖,連接對角線 \(\overline{AC}\),並且設平行四邊形 \(ABCD\) 的面積為 \(x\)
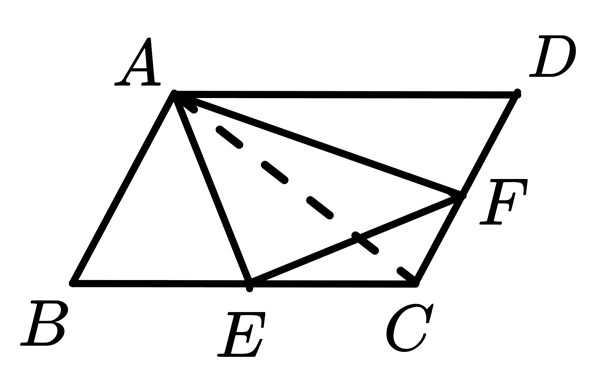
$$\begin{aligned}
\Delta AEF \ 的面積 &= \Delta ACE \ 的面積 + \Delta ACF \ 的面積 – \Delta CEF \ 的面積 \\
&= \frac{1}{4}x+\frac{1}{4}x-\frac{1}{8}x = \frac{3}{8}x
\end{aligned}$$
再動動腦筋,還有什麼解法?
遊戲才剛開始
笛卡兒教我們的,架直角座標系,可以將幾何問題轉為代數問題。
以 \(A\) 點為原點,並且將 \(\overline{OB}\) 置於 \(x\) 軸,然後標上各頂點及線段中點的座標。
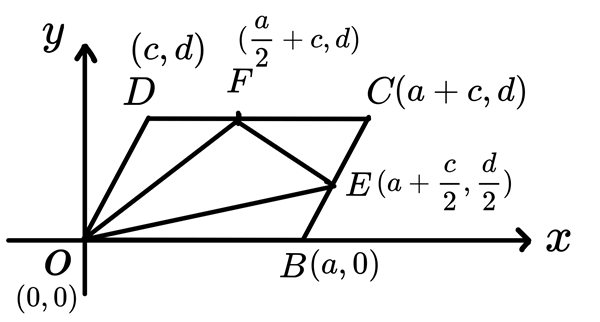
則 \(\Delta OEF 的面積\) 就是由向量 \(\overrightarrow{OE}\) 及 向量 \(\overrightarrow{OF}\) 張出來的三角形面積。
$$\Delta OEF \ 的面積 =\frac{1}{2}\times |
\begin{vmatrix}
a+\frac{c}{2} & \frac{a}{2}+c \\
\frac{d}{2} & d
\end{vmatrix}
| = \frac{3}{8}ad = \frac{3}{8}\ 平行四邊形\ ABCD\ 的面積$$
沿續方法5,既然已經有了座標,我們就可以寫出直線 \(OF\) 的方程式,
進而計算出點 \(E\) 與直線 \(OF\) 的距離。
方法6:直接計算三角形OEF的面積
如圖:

直線 \(OF\) 的方程式為 $$\overleftrightarrow{OF}:dx-(\frac{a}{2}+c)y=0$$ 則
$$d(E, \overleftrightarrow{OF}) = \frac{|d\cdot(a+\frac{c}{2})-(\frac{a}{2}+c)\cdot\frac{d}{2}|}{\sqrt{d^2+(\frac{a}{2}+c)^2}}=\frac{\frac{3}{4}ad}{\overline{OF}}$$ 則 $$\Delta OEF\ 的面積 = \frac{1}{2}\cdot \overline{OF}\cdot \frac{\frac{3}{4}ad}{\overline{OF}}=\frac{3}{8}ad$$ 故
$$\frac{\Delta OEF\ 的面積}{平行四邊形OBCD\ 的面積}=\frac{3}{8}$$
方法7:使用外積的寫法亦可
如圖所示:
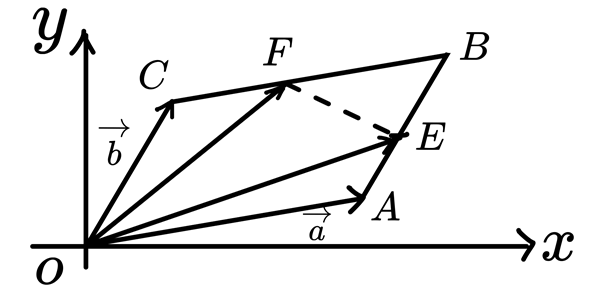
設 $$\overrightarrow{a}=\overrightarrow{OA}\ 且 \ \overrightarrow{b}=\overrightarrow{OC}$$ 則
$$\overrightarrow{OE}=\overrightarrow{a}+\frac{1}{2}\overrightarrow{b},\ \ \overrightarrow{OF}=\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}$$
$$\begin{aligned}
\Delta OEF\ 的面積 &= \frac{1}{2}|\overrightarrow{OE}\times\overrightarrow{OF}| \\
&=\frac{1}{2}|(\overrightarrow{a}+\frac{1}{2}\overrightarrow{b})\times(\frac{1}{2}\overrightarrow{a}+\overrightarrow{b})|\\
&=\frac{1}{2}|\overrightarrow{a}\times \overrightarrow{b}+\frac{1}{4}\overrightarrow{b}\times\overrightarrow{a}|\\
&=\frac{1}{2}\cdot\frac{3}{4}|\overrightarrow{a}\times\overrightarrow{b}|\\
&=\frac{3}{8}|\overrightarrow{a}\times\overrightarrow{b}| = \frac{3}{8}平行四邊形\ OABC\ 的面積
\end{aligned}$$
方法8:線性轉換的觀點
回到方法1,我們考慮了特例:長方形的情況。
處理長方形的面積問題肯定會比一般的平行四邊形簡單。
因此,可以考慮一個線性變換 \(T\),將長方形映射至原問題的平行四邊形,如下圖所示:
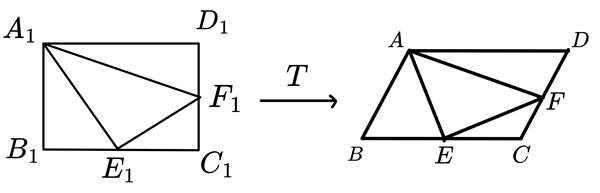
那麼,
$$\begin{aligned}
\frac{\Delta AEF\ 面積}{平行四邊形ABCD\ 面積}&= \frac{|detT|\Delta A_1E_1F_1\ 面積}{|detT|\ 平行四邊形A_1B_1C_1D_1\ 面積}\\
&= \frac{3}{8}
\end{aligned}$$
是否還有其他方法,一定還有,就看你的創意與智慧了。
這篇文章就先寫到這邊,祝學習愉快。





