初學者在學習一個新的單元時,須要做一些基礎題,讓自己熟悉課程內容。
這類題目,只需要很基本的運算,沒有太大的變化。甚至只要簡單的一個步驟就能完成。
通常老師在課堂上,會先帶一些這類的例題,讓同學能掌握住基本概念。
下課後,一定要盡快複習,熟練這些基礎題且保證不會出錯。
往後的學習,就是建立在這些基礎練習上面。
為什麼有些學生,在學了幾堂課之後,突然覺得很困難,跟不太上了?
原因可能就是出在銜接出了問題。
因為沒有盡快複習,遺忘,然後題目層次提高,便開始感到吃力。
在這個階段,基礎題必須練到像呼吸一樣自然,沒別招了。
例如在學習常用對數時,我們要能夠很快判斷以下這些數的值:

或者再稍微變化

這類題目考試通常不考,或考得很少,我們就不再贅述了。
接著進入到下個階段:標準題型演練
這類題目,相較於基礎題計算多一些,解題步驟較多,但不會太困難。
只要將課本或是參考書的題目逐題演練,就會自然而然接觸到很多這個層次的題目。
例如以下這道題目,

這個式子本身就是一個很明顯的提示:要用到立方和公式!
$$\begin{aligned}
原式&=(log2+log5)^3-3log2\cdot log5\cdot(log2+log5)+3log5\cdot log2 \\
&=1-3log2\cdot log5 +3log5\cdot log2 \\
&=1
\end{aligned}$$ 當然,如果同學忘了立方和公式,這一題就會不知如何處理了。
再來看幾題這個階段的題目

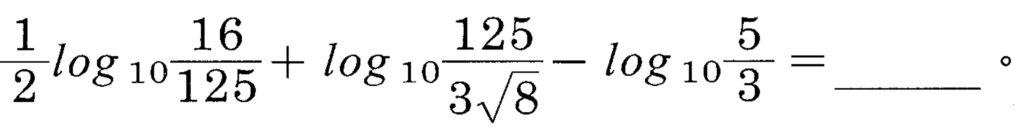

通常這類型的題目可以掌握好,考試及格是沒有太大的問題了。
第三種是進階思考題,就是那些我們比較少看過的題目。
尤其大考題,很多題目是命題教師的原創,
我們平常不可能看過。我們拿到考卷的第一眼感覺必定是很陌生。
舉個例子來看看吧:

所以對於偏重記憶型學習法的學生,可能會不知所措,怎麼跟平常看到的題目不太一樣?
其實這只是將數字換個寫法而已,例如 $$235864 = 2\times 10^5 + 3\times 10^4 + 5\times 10^3 + 8\times 10^2 + 6\times 10 + 4$$
也就是說,題目只是要我們這個數字的「位數」,而 \(n = 位數 -1\)
這類題目不一定是困難的,只是平常要多思考,構築出自己的解題策略。
然後抽絲剝繭,慢慢找出答案。
即使沒解出來,也可以累積經驗,強化自己的解題策略。
如何判斷自己是不是真的理解?
一個重要指標就是,能不能解出那些沒見過的題目。
這類題目,也是在考試時分出勝負的關鍵。
所以學習數學時,在每一道題演練的過程中,
一定要牢記,目標是要建立出自己的解題策略,
而不是反射性動作般地重複演算,看到須要思考的題目,
卻反而輕易看詳解,失去了磨練自己的機會。
當然,對於每個階段,何謂基礎題?何謂標準題?何謂思考題?會有所不同。
我們前面看的那一題思考題,一旦有了經驗,是不是就變成標準題甚至是基礎題了呢?
但是還有一種很慘的情況,就是課後沒有盡快複習,觀念遺忘。
然後看基礎題也彷彿是進階題,事倍功半。這時候還一直在逐題看詳解,
陷入一種無效的學習模式,浪費寶貴的時間。