花了一些時間，將整份試題寫了一遍。今年這份考題難度適中，以下附上試題與解答連結。

內容目錄

歡迎訂閱高中數學數位學習電子報

高中數學數位學習電子報

數學數位學習教室入口

試題解析

第1題：三角函數基礎題

這一題只要用三角函數的定義即可解出。

如下圖所示：

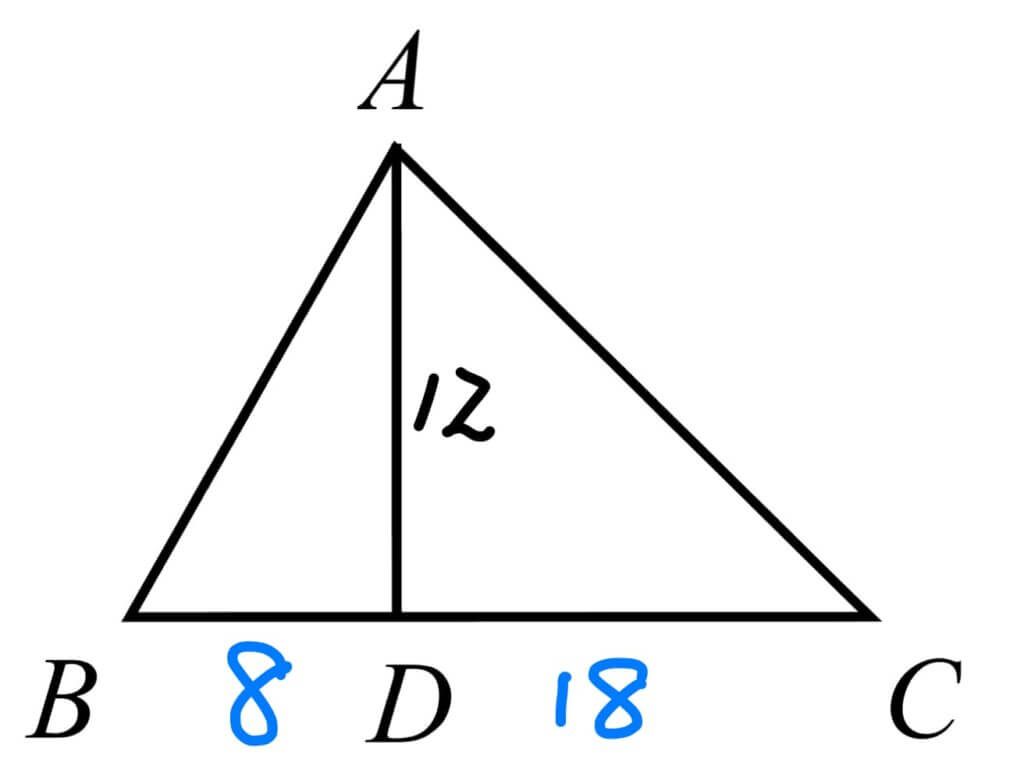
在 $\Delta ABD$ 中，因為 $\overline{AD}=12$ ，且 $tan\angle{B}=\frac{3}{2}$ ，則 $\overline{BD}=12\cdot \frac{2}{3}=8$

同樣地，在 $\Delta ACD$ 中， $\overline{CD}=12\cdot \frac{3}{2}=18$ 因此 $\overline{BC}=8+18=26$

第2題：橢圓的伸縮對方程式的影響

設經過伸縮後，新圖形的座標為 $(x’, y’)$

因此
$\begin{bmatrix} x’ \\ y’ \end{bmatrix}= \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} 2x \\ 3y \end{bmatrix}$ 將 $x=\frac{1}{2}x’, y=\frac{1}{3}y’$ 代回 $\Gamma$ 方程式： $\frac{1}{a^2}\cdot\frac{1}{4}x’^2+\frac{1}{6^2}\cdot\frac{1}{9}y’^2=1$
接著將點 $(18,0)$ 代入可得 $\frac{1}{4a^2}\cdot 18^2=1 \ \ \Longrightarrow \ \ a^2=9^2$

這是一個「躺著」的橢圓，並且 $c^2=9^2-6^2=45$

因此可得其焦點座標為 $(\pm 3\sqrt{5}, 0)$ 。

建議可以自己畫個圖會看得更清楚。

第3題：排列組合

我們可以分成兩種情況處理：

情況一：畫X列不擺 (也就是第一列不擺)

那麼這四個棋子必須在2~5列各放1個，每一列有5行。5行中選出4行放這4個棋子，例如：

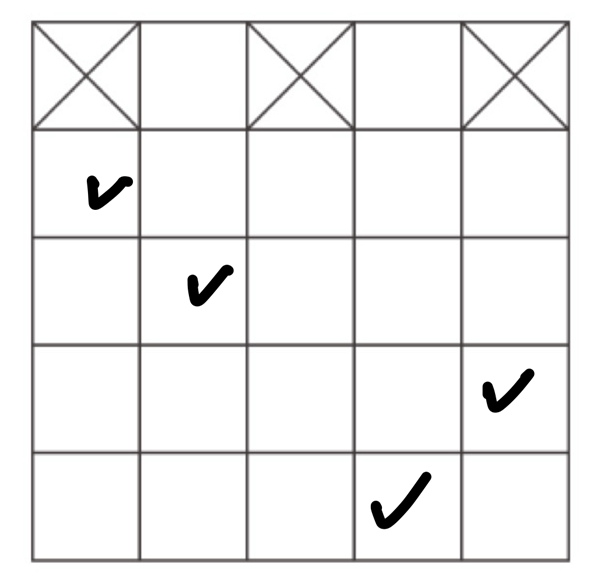
擺放方式有 $P^5_4=120$ 種。

情況二：畫X列有擺。也就是說，第一列必須擺1個棋子。

第一列擺了1個棋子後，還有3個棋子，放在其中3列( $C^4_3$ )，然後再從4行中選3行放入棋子( $P^4_3$ )，例如：

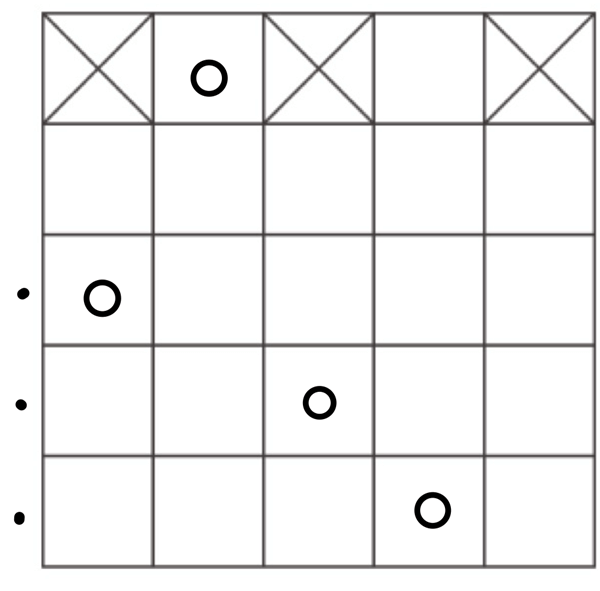
擺放方式有 $C^4_3\cdot P^4_3\cdot 2=192$

合計＝ $120+192=312$ ，答案選(4)

第4題：求期望值

選項(1)：中獎一次，但是要抽幾次呢？可能1次、2次、3次、…都要考慮，所以會寫出一個無窮級數如下：
$E=1\cdot \frac{1}{10}+2\cdot(\frac{9}{10})\cdot(\frac{1}{10})+3\cdot(\frac{9}{10})^2\cdot(\frac{1}{10})+…\tag{1}$

這是一個”差比”級數，也就是當中有等差及等比的部份，這種級數的求和方式就是同乘以”公比的部份”
$\frac{9}{10}\cdot E=(\frac{9}{10})\cdot(\frac{1}{10})+2\cdot(\frac{9}{10})^2\cdot(\frac{1}{10})+…\tag{2}$
將第(1)式減去第(2)式可得：
$\begin{aligned} \frac{1}{10}E &= \frac{1}{10}+\frac{9}{10}\cdot\frac{1}{10}+(\frac{9}{10})^2\cdot(\frac{1}{10})+…\\ &= \frac{\frac{1}{10}}{1-\frac{9}{10}}=1 \end{aligned}$

因此 $E=10$ 選項(1)正確。

選項(2)：可理解為，甲抽獎兩次，至少中獎一次的機率，可採用反面做法： $P(至少中一次)=1-P(兩次未中)=1-(\frac{9}{10})^2=\frac{19}{100}$ 此選項錯誤。

選項(3)：10次都沒中的機率為 $(\frac{9}{10})^10$ ，抽獎1次就中獎的機率為 $\frac{1}{10}$ ，兩數可以取log比大小：
$log(\frac{9}{10})^{10}=10\cdot log\frac{9}{10}=10\cdot (log9-1)=10\cdot(-0.0458)=-0.458>log\frac{1}{10}$ 此選項錯誤。

選項(4)：我們來估算一下，假設甲至少要存 $n$ 個代幣才能保證中獎機率大於0.9，即 $1-(\frac{9}{10})^n>\frac{9}{10}$
移項整理：
$\begin{aligned} (\frac{9}{10})^n < \frac{1}{10}\ \ \Longrightarrow \ \ n\cdot (log9-1)<-1 \ \ \Longrightarrow \ \ n>\frac{1}{0.0458}\approx 21.xx \end{aligned}$ 此選項正確。

選項(5)：無論存再多的代幣，還是有限個，那麼保證中獎機率會接近1，但不可能為1。

第5題：三次多項式與方程式

選項(1)：由虛根成對定理可知， $f(-2+3i)=0$ ，此選項錯誤。

選項(2)：顯然正確。我們可以將這個多項式寫出來：
$\begin{aligned} 令 \ f(x) &= (x^2+4x+13)(ax+b) \\ &= (x+2)(x-1)Q(x)+18 \end{aligned}$ 依條件列式
$\begin{cases} 18 = f(-2) = 9\cdot (-2a+b) \\ 18 = f(1) = 18\cdot (a+b) \end{cases}$ 解得
$\begin{cases} a=-\frac{1}{3} \\ b=\frac{4}{3} \end{cases}$ 因此 $f(x)$ 的三次項係數為負，選項(3)正確。

選項(4)： $0=f(x)=(x^2+4x+13)(-\frac{1}{3}x+\frac{4}{3}) \ \ \Longrightarrow \ \ x=-2\pm 3i, 4$ 此選項正確。

選項(5)： $f(x)=(x^2+4x+13)(-\frac{1}{3}x+\frac{4}{3})=-\frac{1}{3}x^3+x+\frac{52}{3}$ 對稱中心為 $(0,\frac{52}{3})$ ，應該是在 $y$ 軸上，此選項錯誤。最後答案選(2)(3)(4)

第6題：空間向量活用題

選項(1)：先根據內積與外積的定義列式：
$\begin{cases} |\overrightarrow{u}||\overrightarrow{v}|cos\theta=\sqrt{15} \tag{3}\\ |\overrightarrow{u}||\overrightarrow{v}|sin\theta=\sqrt{(-1)^2+0^2+3^2}=\sqrt{10} \end{cases}$

為了求出夾角，可將以上兩式相除：
$tan\theta=\frac{|\overrightarrow{u}||\overrightarrow{v}|sin\theta}{|\overrightarrow{u}||\overrightarrow{v}|cos\theta}=\sqrt{\frac{2}{3}}<1$ 因此 $0<\theta<\frac{\pi}{4}$ 此選項錯誤。

選項(2)：因為 $(-1,0,3)\cdot (1,0,-1)\neq 0$ 所以向量 $\overrightarrow{u}$ 不可能為 $(1,0,-1)$ ，此選項錯誤。

選項(3)：將第(3)式的上下兩式平方相加： $|\overrightarrow{u}|^2|\overrightarrow{v}|^2(cos^2\theta+sin^2\theta)=25 \ \ \Longrightarrow \ \ |\overrightarrow{u}||\overrightarrow{v}|=5 \tag{4}$ 接著由算幾不等式可知 $\frac{|\overrightarrow{u}|+|\overrightarrow{v}|}{2}\geq \sqrt{|\overrightarrow{u}||\overrightarrow{v}|}\ \ \Longrightarrow \ \ |\overrightarrow{u}|+|\overrightarrow{v}|\geq 2\sqrt{5}$ 此選項正確。

選項(4)：因為向量 $\overrightarrow{v}$ 以及角度 $\theta$ 已確定，因此向量 $\overrightarrow{u}$ 的方向也被確定了。

另外，由第(4)式可知， $|\overrightarrow{u}|=\frac{5}{|\overrightarrow{v}|} \ \ 已確定$

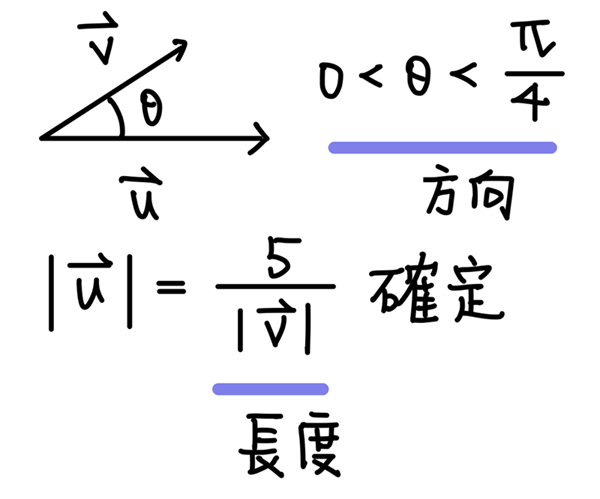
故 $|\overrightarrow{u}|$ 可以被唯一決定，此選項正確。

選項(5)：令 $|\overrightarrow{u}|+|\overrightarrow{v}|=k$ 則 $|\overrightarrow{v}|=k-|\overrightarrow{u}|\tag{5}$

接著將第(5)式同乘以 $|\overrightarrow{v}|$ 可得 $|\overrightarrow{v}|^2-k|\overrightarrow{v}|+5=0$

$|\overrightarrow{v}|$ 是唯一的充要條件為 $k^2-20=0$ ，故此選項不正確。最後答案選(3)(4)。

第7題：多項函數與三角函數的圖形特徵

選項(1)：可以先算函數 $f(x)$ 的導函數： $f'(x)=5x^4-15x^2+10x$ 因此 $f'(1)=0$ 此選項正確。

選項(2)：要看函數的單調性，只要觀察其一次導函數即可
$\begin{aligned} f'(x) &= 5x (x^3-3x+2) \\ &= 5x(x-1)^2(x+2) \end{aligned}$ 畫個表格觀察一下：

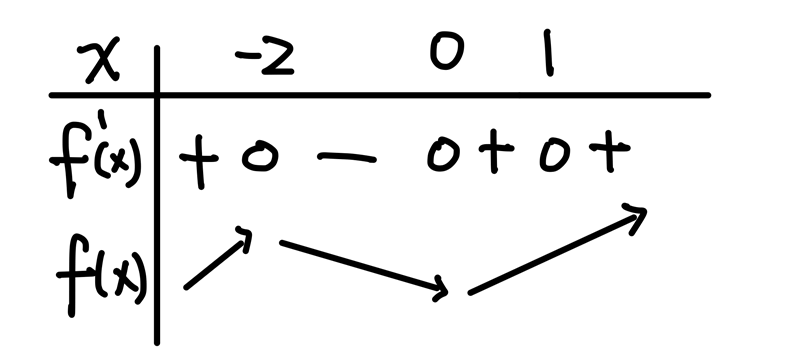
很明顯地，函數 $y=f(x)$ 在區間 $[0,2]$ 遞增，此選項正確。

選項(3)：函數圖形的凹口要看二次導函數
$\begin{aligned} f”(x) &= 20x^3-30x+10 \\ &= 10(2x^3-3x+1) \\ &= 10\cdot (x-1)(2x^2+2x-1) \end{aligned}$ 同樣地，畫個表格觀察：

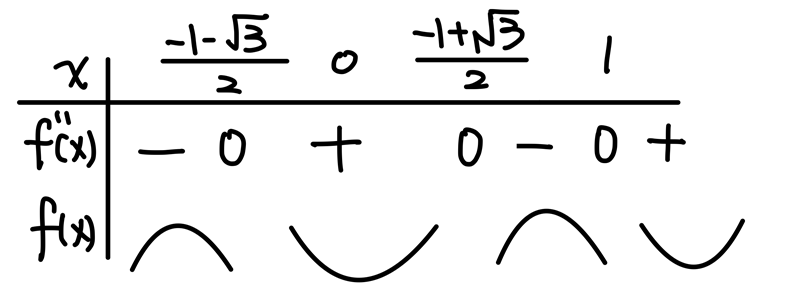
此選項錯誤。

選項(4)：已知 $g(x)=sin(\frac{\pi x}{3}+\frac{\pi}{2})=cos(\frac{\pi x}{3})$ 接著 $g(x+6\pi)=cos(\frac{\pi(x+6\pi)}{3})=cos(\frac{\pi x}{3}+2\pi^2)\neq g(x)$ 此選項錯誤。

選項(5)：同樣地，觀察 $y=f(x)$ 的一次導函數即可判斷其單調性：

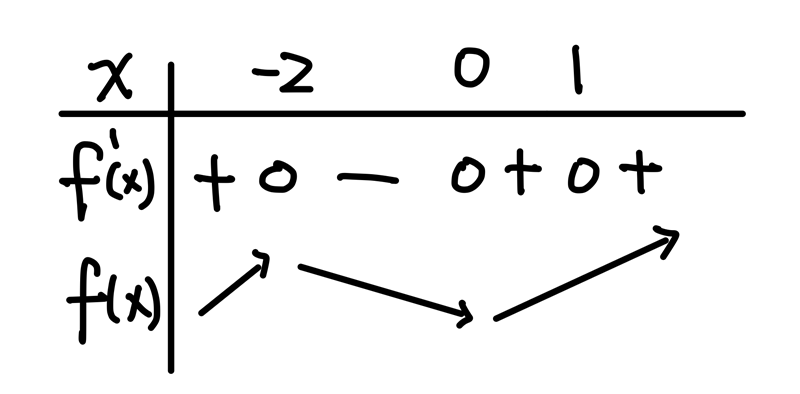
因此函數 $y=f(x)$ 在閉區間 $[3,4]$ 遞增。

另外，函數 $y=g(x)$ 的簡圖如下：

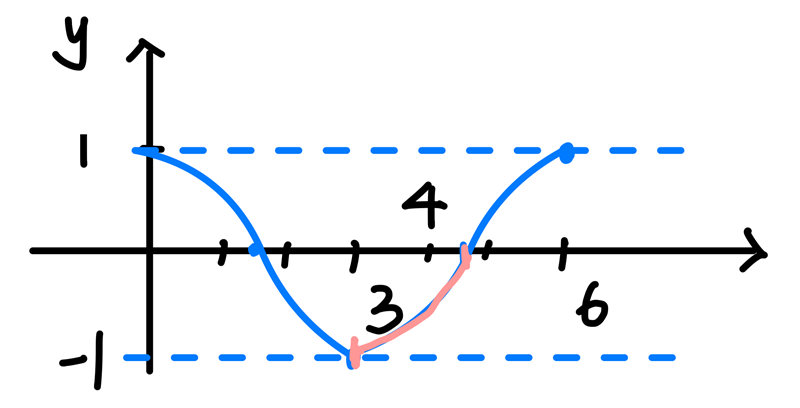
同樣地，函數 $y=g(x)$ 在閉區間 $[3,4]$ 遞增，因此選項(5)正確。最後答案選(1)(2)(5)

請【登入網站】即可觀看完整內容。

若還沒有帳號，請先【註冊】成為網站會員。

第8題：複數的極式與無窮數列混合題

為了方便操作，我們可以先寫下複數的極式 $z=\alpha(cos\beta+isin\beta) \ \ \Longrightarrow \ \ z^n=\alpha^n(cos{n\beta}+isin{n\beta})$

選項(1)：將 $\alpha=1$ ， $\beta=\frac{3\pi}{7}$ 代入可得 $x_{10}=cos{\frac{30}{7}\pi=cos{\frac{2}{7}\pi}}$
$x_3=cos{\frac{9}{7}\pi}=-cos{\frac{2}{7}\pi}$ 故 $x_{10}\neq x_3$ 此選項錯誤。

選項(2)： $0=y_3=\alpha^3sin{3\beta} \Longrightarrow \ \ 3\beta=k\pi,\ k\in Z$
因此 $y_6=\alpha^6sin{6\beta}=\alpha^6sin{2k\pi}=0$ 此選項正確。

選項(3)：可以舉一個反例 $\alpha=\sqrt[3]{2}, \beta=\frac{\pi}{6}$ 得到 $x_3=1, x_6=-4\neq 1$ 此選項錯誤。

選項(4)：同樣地，可以舉一個反例： $\alpha=2, \beta=\pi$ 此選項錯誤。

選項(5)： $\alpha^ncos{n\beta}\ \ 收斂 \ \ \Longrightarrow \ \ \alpha=1, \beta=0 \ \ or\ \ \alpha<1, 0\leq \beta<2\pi$

因此 $y_n=\alpha^nsin{n\beta} \ \ 收斂$ 此選項正確，最後答案選(2)(5)

第9題：解二元一次聯立方程式

接著進行選填題的部份，第9題只是基本的計算題，我用矩陣的寫法寫一次：

由題目的條件可知，聯立方程式
$\begin{cases} ax+by=2 \\ cx+dy= 1 \tag{6} \end{cases}$ 的解為
$\begin{cases} x= 5 \\ y= 2 \end{cases}$

聯立方程式
$\begin{cases} ax+by=-1 \\ cx+dy=-1 \tag{7} \end{cases}$ 的解為
$\begin{cases} x= 1 \\ y= -1 \end{cases}$

將以上兩組解代入原聯立方程式可得
$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} 5 & 1 \\ 2 & -1 \end{bmatrix} = \begin{bmatrix} 2 & -1 \\ 1 & -1 \end{bmatrix}$

接著，將以上方程式同乘以
$\begin{bmatrix} 5 &1 \\ 2 & -1 \end{bmatrix}\ \ 的反矩陣$
但是先不要將此反矩陣算出來
$\begin{bmatrix} a &b \\ c & d \end{bmatrix}= \begin{bmatrix} 2 &-1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} 5 & 1 \\ 2 & -1 \end{bmatrix}^{-1}$
接著，
$\begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1}= \begin{bmatrix} 5 & 1 \\ 2 & -1 \end{bmatrix} \begin{bmatrix} 2 & -1 \\ 1 & -1 \end{bmatrix}^{-1}= \begin{bmatrix} 6 & -7 \\ 1 & 0 \end{bmatrix}$
最後可以解題目要求的聯立方程式了
$\begin{cases} ax+by=0 \\ cx+dy=1 \end{cases}$
將此方程式改寫為矩陣的形式
$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$
因此
$\begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1} \begin{bmatrix} 0 \\ 1 \end{bmatrix}= \begin{bmatrix} 6 & -7 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix}= \begin{bmatrix} -7 \\ 0 \end{bmatrix}$

第10題：圓與直線的關係

為了更好了解題意，可以先畫個圖看看：

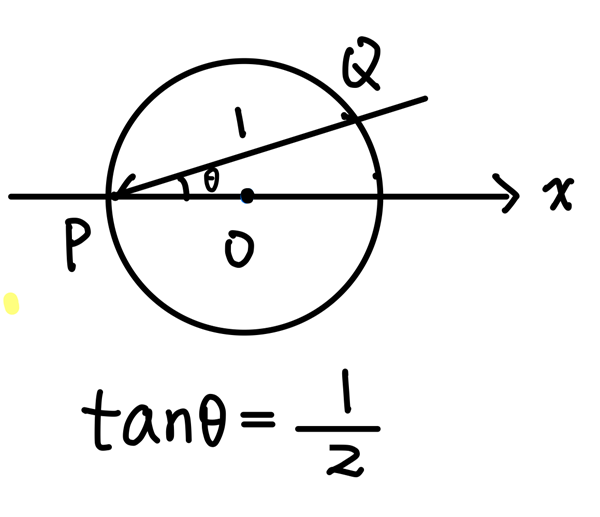
這個圓的直徑落在 $x$ 軸上，假設 $P$ 點坐標為 $(-r,0)$ 且直線 $PQ$ 的斜角為 $\theta$ 且方程式為 $x-2y=-r$

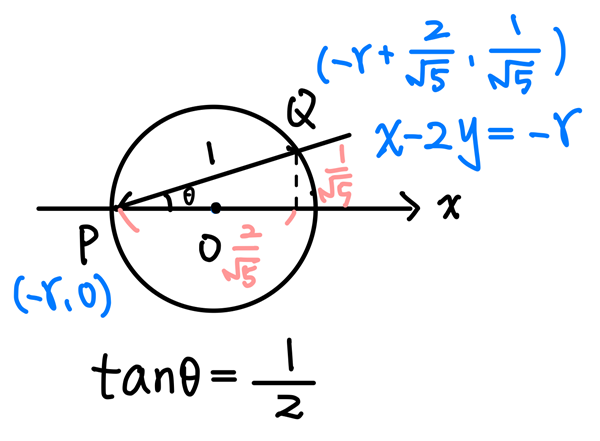
由上圖所示，可以寫出 $Q$ 點的坐標為 $(-r+\frac{2}{\sqrt{5}}, \frac{1}{\sqrt{5}})$

接著要設法將半徑 $r$ 算出來。

可以將 $Q$ 點代入圓方程式：
$(-r+\frac{2}{\sqrt{5}})^2+(\frac{1}{\sqrt{5}})^2=r^2 \ \ \Longrightarrow \ \ -\frac{4}{\sqrt{5}}r+1=0$ 最後解得 $r=\frac{\sqrt{5}}{4}$

第11題：對數構成的等差數列

首先，依題意可知， $log_2b$ 是 $log_2{a_3}$ 與 $log_2{a_9}$ 的等差中項，因此
$log_2{a_3}+log_2{a_9}=2log_2b \ \ \Longrightarrow \ \ log_2a_3\cdot a_9 = log_2 b^2$ 將對數捨去，可得
$a_3\cdot (a_3+12)=(a_3+2n)^2, \ 1\leq n \leq 5$ 接著去掉括號 $a_3^2+12a_3=a_3^2+4na_3+4n^2$
移項整理： $(12-4n)a_3=4n^2$
如果 $n=1$ ，則 $a_3=\frac{1}{2}$ ，這個答案沒問題。

如果 $n=2$ ，則 $a_3=4$ ，這個答案不行，為什麼？
因為這會造成 $a_1=0$ ，與原意題不符合。

如果 $n=3,4,5$ ，這會造成 $a_3<0$ ，也不用考慮了。

最後答案 $a_9=a_3+6\cdot 2 = \frac{1}{2}+12=\frac{25}{2}$

第12題：求三平面兩兩交線的共同交點

求三直線的共同交點，就是求出三平面的共同交點，可以用高斯消去法進行矩陣的列運算如下：

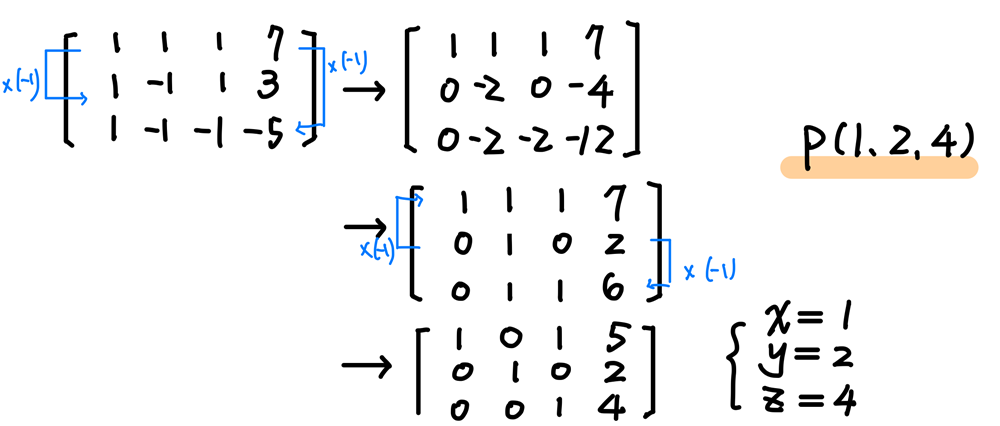
第13題：求直線的夾角

為了求出三直線兩兩所夾銳角，必須先寫出其方向向量：
$\begin{aligned} \overrightarrow{L_1} \ &// \ (1,-1,1)\times (1,-1,-1) = (2,2,0) // (1,1,0) \\ \overrightarrow{L_2} \ &// \ (1,1,1)\times (1,-1,-1) = (0,2,-2) // (0,1,-1) \\ \overrightarrow{L_3} \ &// \ (1,1,1)\times (1,-1,1) = (2,0,-2) // (1,0,-1) \\ \end{aligned}$

接著來計算三個度角的餘弦值：
$cos\alpha = \frac{\overrightarrow{L_1}\cdot\overrightarrow{L_2}}{|\overrightarrow{L_1}||\overrightarrow{L_2}|}=\frac{(1,1,0)\cdot (0,1,-1)}{\sqrt{2}\cdot\sqrt{2}}=\frac{1}{2}$
$cos\beta = \frac{\overrightarrow{L_2}\cdot\overrightarrow{L_3}}{|\overrightarrow{L_2}||\overrightarrow{L_3}|}= \frac{(0,1,-1)\cdot (1,0,-1)}{\sqrt{2}\cdot\sqrt{2}}=\frac{1}{2}$
$cos\gamma = \frac{\overrightarrow{L_3}\cdot\overrightarrow{L_1}}{|\overrightarrow{L_3}||\overrightarrow{L_1}|}= \frac{(1,0,-1)\cdot (1,1,0)}{\sqrt{2}\cdot\sqrt{2}}=\frac{1}{2}$

因此 $\alpha=\beta=\gamma=60^{\circ}$

第14題：求正四面體中某一面的方程式

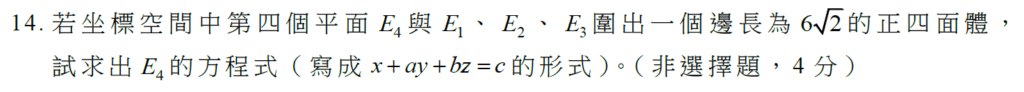
這題是這個題組最有趣的一題，先畫個圖來看一下：

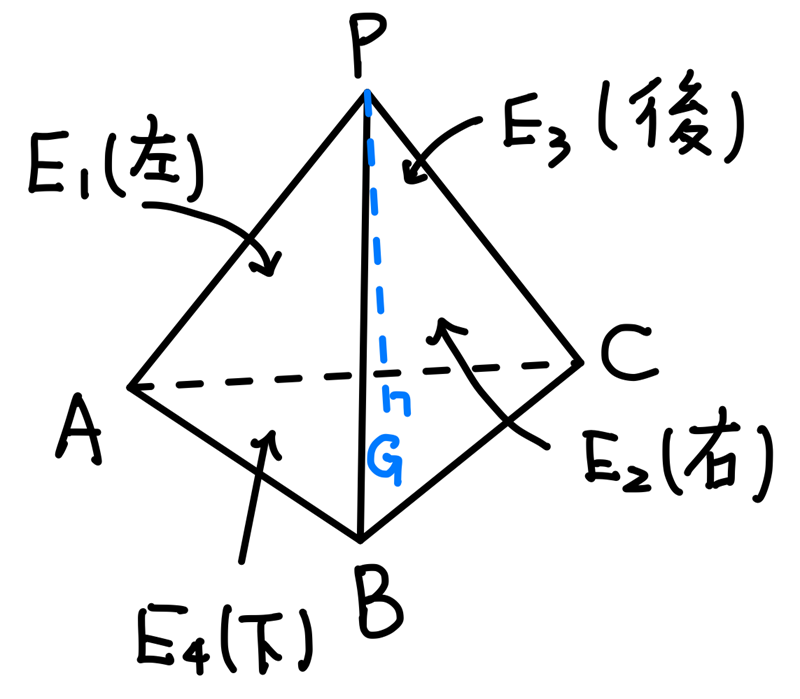
因為這是一個正四面體，所以過 $P$ 點作的高會通過三角形 $ABC$ 的重心 $G$ ，其中要注意的是
$\begin{cases} \overrightarrow{PA} = (0,6,-6) \\ \overrightarrow{PB} = (6,0,-6) \\ \overrightarrow{PC} = (6,6,0) \end{cases}$

由重心的向量性質可知
$\begin{aligned} \overrightarrow{PG} &= \frac{1}{3}\overrightarrow{PA} + \frac{1}{3}\overrightarrow{PB} + \frac{1}{3}\overrightarrow{PC} \\ &= \frac{1}{3}(0,6,-6)+\frac{1}{3}(6,0,-6)+\frac{1}{3}(6,6,0) \\ &= (4,4,-4) // (1,1,-1) \end{aligned}$ 現在有了 $P$ 點及方向向量 $(1,1,-1)$ ，可以令點 $G$ 的坐標為 $(1+t, 2+t, 4-t)$
由正四面體的高算出 $t$ ： $(\frac{\sqrt{6}}{3}\cdot 6\sqrt{2})^2=\overline{PG}^2=t^2+t^2+t^2$ 解得 $t=\pm 4$ 因此 $G(5,6,0) \ \ or \ \ G(-3,-2,8)$
最後可求出平面 $E_4$ 的方程式 $E_4: x+y-z=11 \ \ or \ \ x+y-z=-13$

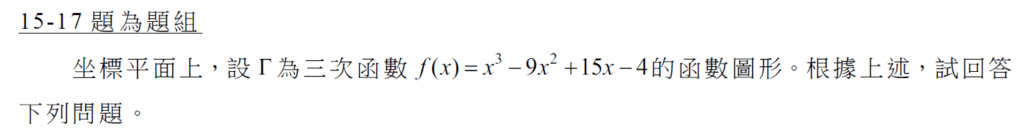
第15題：求多項式的導函數

這一題是送分題： $f'(x)=3x^3-18x+15$ 答案選 (4)

第16題：求過某一點的切線方程式

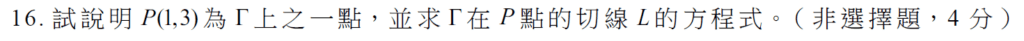
這一題也是送分題。此直線在 $P$ 點的斜率為 $f'(1)=3-18+15=0$ 因此直線 $L$ 的方程式為 $y=3$

第17題：求曲線與直線圍出來的區域面積

這一題的圖形不太好畫，不過大概畫一下就好，最主要是直線 $L$ 與曲線 $\Gamma$ 的交點坐標不能算錯

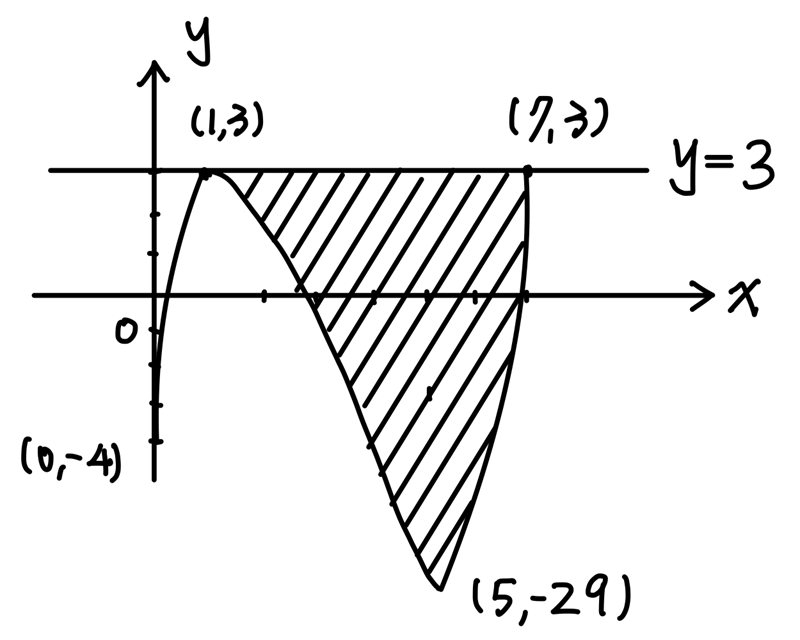
$\begin{aligned} 斜線部份面積 &= \int_1^7 3-(x^3-9x^2+15x-4) dx \\ &= \int_1^7 (-x^3+9x^2-15x+7) dx \\ &= 108 \end{aligned}$

寫完了，這份試題難度適中，分享個人解題觀點給大家，若有謬誤，歡迎提出指正，感謝。

【教學】113年分科測驗數甲試題解析