最近高中課程即將進行到第2冊。
我們來談談第一節：數列
你覺得這個單元的精神是什麼？
我認為是培養「觀察」、「猜測」與「驗證」的能力。
首先我們來看一道，從國小到高中以及一些邏輯測驗常見的問題：
請觀察以下數列的規則，判斷第\(6\)項的數字\(\bigtriangleup\)是多少？
$$1, 2, 4, 8, 16, \bigtriangleup$$ 大多數人的第一反應就是 \(32\)，因為從這個數列的前幾項，看起來很像公比為 \(2\) 的等比數列。
實則不然
如果這個數列沒有指定一般項，那麼第 \(6\) 項可以是任何數字。
為什麼？
例如：$$a_n = 2^{n}+(n-1)(n-2)(n-3)(n-4)(n-5)\cdot \frac{K- 64}{120}$$ 那麼我們可以得出第 \(6\) 項 \(a_6=K\)，其中 \(K\) 可以是任何數。
換句話說，每個人可能因為主觀看到的規則不同，
而得出不一樣的答案，這是個不嚴謹的問題。
所以下次當你遇到這類題目，困擾為什麼自己的答案總是與解答不同時，
不用擔心，這不是你的問題，而是題目本身就有瑕疵。
最嚴謹的答案其實是「任意數」。
那麼，什麼樣的問題才是一個好的問題呢？
在翰林版課本裡，提到一道有趣的題目：
考慮一圓，圓周上有 n 個相異的點，任何兩點皆以線段連接。
假設沒有三點共線的情形，則這些線段可以將圓分割成幾個區域？
不妨試著畫看看：
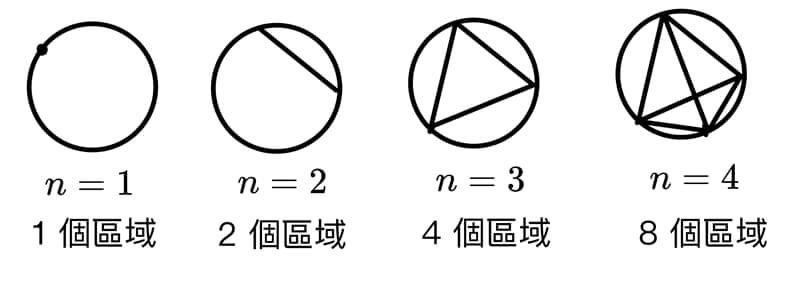
設 \(a_n\) 為 \(n\) 個點時，連接線段將圓分割的區域數，目前看來此數列的前四項為 1, 2, 4, 8
似乎是首項為 \(1\)，公比為 \(2\) 的等比數列，猜測 \(a_n=2^n \)
為了謹慎起見，再多畫幾個看看：
在第 \(6\) 項的時候出現不合群的一項，竟然只有 \(31\) 個區域，所以我們猜錯了。
附帶一提，在畫圖的時候，可能會三點共線，
此時分割出來的區域數會比較少。
因此原命題才會假設「沒有三點共線的情形」，
這樣才能確保分割出來的區域數是最多的。
這個問題也提醒我們，不能單從觀測前幾項就斷定這個數列的一般項，
必須真的看出規則才行。
課本在此就打住了，沒有繼續寫下去，我們接著繼續探討，
這個問題應該怎麼處理，提供給有興趣的同學參考。
首先，觀察一下，當圓周上每增加一點時，區域數會有什麼樣的變化？
以目前六項來看：$$a_1=1, a_2=2, a_3=4, a_4=8, a_5=16, a_6=31$$則
$$\begin{aligned}
\Delta a_1 &=a_2-a_1 =1 \\
\Delta a_2 &=a_3-a_2 =1+1 \\
\Delta a_3 &=a_4-a_3 =1+2+1 \\
\Delta a_4 &=a_5-a_4 =1+3+3+1 \\
\Delta a_5 &=a_6-a_5 =1+4+5+4+1 \\
\end{aligned}$$ 有點像巴斯卡三角形，而且每一斜列似乎是有規律的：
每個斜列都是一個等差數列，我將其一般項寫出來看一下：
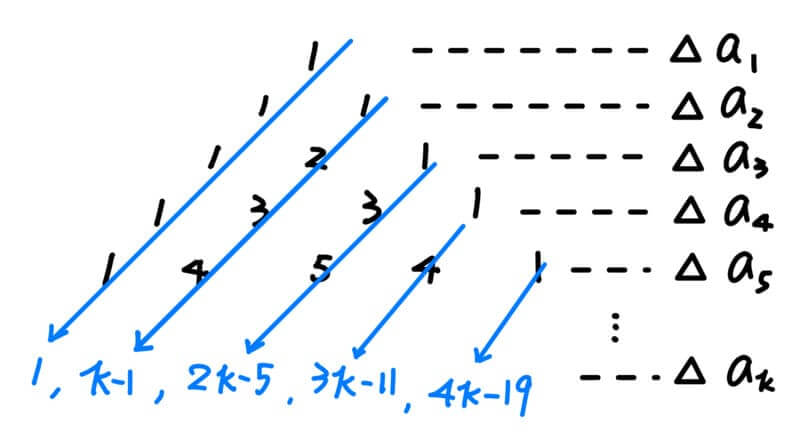
第 \(k\) 列的第 \(j\) 項要如何表示呢？
依據規則可知，$$(j-1)k-[j(j-1)-1]$$ 化簡可得 $$(j-1)(k-j)+1, j=1,2,3,…,k$$ 也就是說，當圓周上有 \(k\) 個點，再多增加一個點時，會增加區域數$$\Delta a_k = \sum_{j=1}^k[(j-1)(k-j)+1]$$ 接著將其累加可得：
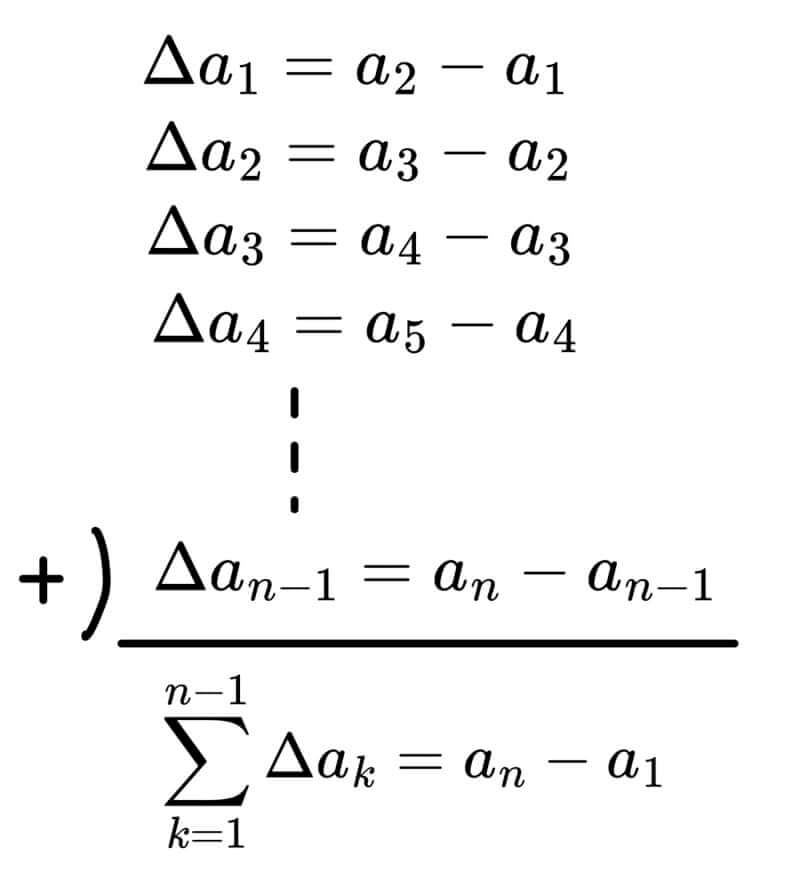
因此
$$\begin{aligned}
a_n &= a_1+\sum_{k=1}^{n-1}\Delta a_k \\
&=a_1+\sum_{k=1}^{n-1}\sum_{j=1}^n[(j-1)(k-j)+1]\\
&=1+\sum_{k=1}^{n-1}\frac{k^3-3k^2+8k}{6}\\
&=1+\frac{1}{24}n(n-1)(n^2-5n+18)
\end{aligned}$$
以上的計算不難，但須要一些耐心，可單獨作為一道習題了。
有了以上式子，不妨代幾項看看是否正確：$$a_1=1, a_2=2, a_3=4, a_4=8, a_5=16, a_6=31$$ 太棒了，前六項都沒錯。
問題來了，那麼要怎麼確認每一項都是對的呢，總不可能一直畫圖確認吧？
此時就要用到「數學歸納法」
首先，\(n=1\) 時顯然成立。
假設前 \(n\) 項時皆成立，即 $$a_n=\frac{1}{24}n(n-1)(n^2-5n+18)+1$$ 那麼增加至第 \(n+1\) 個點時，區域數會增加多少呢？
首先，我們先要有一個觀念：當圓內各點每多連一條線，就會多增加一個區域；兩直線每增加 \(1\)個交點，會再多一個區域。
也就是說，決定區域數，其實就是在決定可連成幾條直線，以及有多少個交點。
如果你不知道為什麼，不妨畫幾個圖觀察就會知道了。
如下圖，我們考慮在圓上原本 \(n\) 個點中，再增加第 \(n+1\) 個點 \(P_{n+1}\) 時，會多出幾個區域。
首先，將 \(P_{n+1}\) 與 \(P_j\) 相連，其中 \(j=1,2,3,…,n\)
那麼線段 \(\overline{P_{n+1}P_j}\) 會將圓隔成兩部份，分別為上半部：\(P_1, P_2, P_3, …,P_{j-1}\) 與 下半部：\(P_{j+1}, P_{j+2}, …, P_{n}\)
將上半部的 \(j-1\) 個點與下半部的 \(n-j\) 個點相連，與線段 \(\overline{P_{n+1}P_j}\) 會有 \((j-1)(n-j)\) 個交點。
如下圖所示(示意圖)：
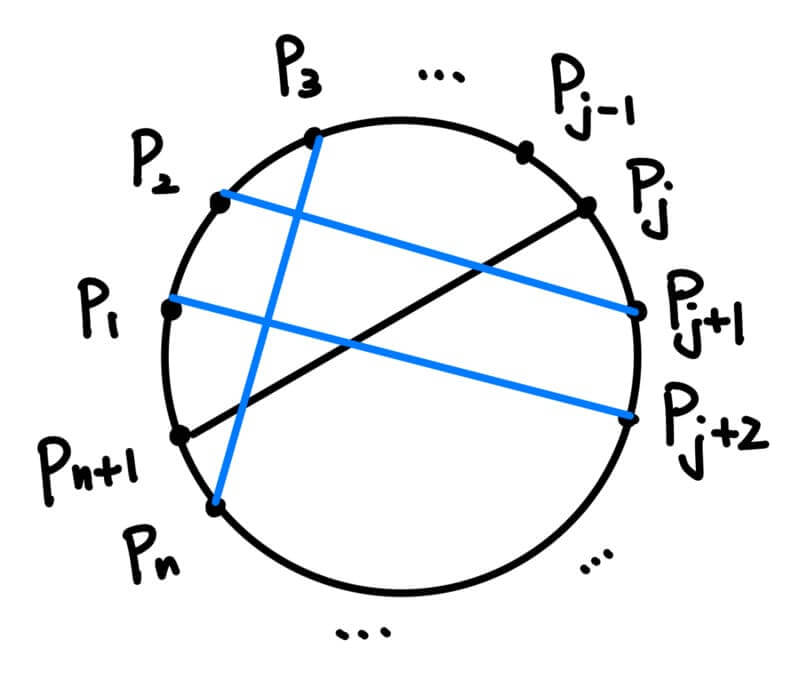
也就是說，總區域數增加 $$(j-1)(n-j)+1$$ 再將其加總 \(j=1,2,3,…,n\) 可得 $$\sum_{j=1}^n [(j-1)(n-j)+1]=\frac{1}{6}(n^3-3n^2+8n)$$
因此 $$\begin{aligned}
a_{n+1} &= a_n+\frac{1}{6}(n^3-3n^2+8n) \\
&= \frac{1}{24}n(n-1)(n^2-5n+18)+1+\frac{1}{6}(n^3-3n^2+8n) \\
&= \frac{1}{24}n\cdot[(n-1)(n^2-5n+18)+4(n^2-3n+8)]+1\\
&= \frac{1}{24}n\cdot[n^3-2n^2+11n+14]+1\\
&= \frac{1}{24}n(n+1)(n^2-3n+14)+1\\
&= \frac{1}{24}n(n+1)[(n+1)^2-5(n+1)+18]+1
\end{aligned}$$
great!
因此由數學歸納法得知，$$a_n=\frac{1}{24}n(n-1)(n^2-5n+18)+1, \forall \ n \in N$$
以上就是我們在學習數學時時常經歷的過程：問題 -> 發現 -> 猜測 -> 證明
教科書篇幅有限，無法對此有太多的闡述，同學們還是要多找一些科普書籍閱讀，
才有助於提升思考的廣度與深度。
最後，提供這一題比較快捷的解法：
因為任何兩點決定一直線，故 \(n\) 個點可決定 \(C^n_2\) 條直線，如果它們在圓內彼此不相交，
則可以將圓分割成 \(1+C^n_2\) 個區域。另外，任何四個點可圍成一個四邊形，其對角線會決定一個交點，
而每多一個交點就會多一個區域，因此 $$a_n=1+C^n_2+C^n_4=1+\frac{n(n-1)}{24}(n^2-5n+18)$$
這篇文章就先寫到這邊，希望能帶給你一些啟發。
歡迎訂閱高中數學數位學習電子報，
我會在每週一早上寄e-mail至你的信封，與你分享數學學習的方法與心得。[/urcr_restrict]
高中數學數位學習電子報
No comments! Be the first commenter?