大部份有趣的數學都不是寫在教科書裡

為此，我鼓勵學生多讀課外書，會發現截然不同的數學世界。

這一篇文章，我要來探討「無窮」這個讓學生感到新奇的概念。
請注意，無窮是概念，而不是數字。

一個常見的例子，$0.\overline{9}$ 與 $1$ 哪個數字較大？

大多數學生會回答，$1$ 比較大，極少數學生會回答一樣大，還有幾位調皮搗蛋的會說 $0.\overline{9}$ 比較大。

簡單來說，因為 $\frac{1}{3}=0.\overline{3}$，所以 $$1=3\times \frac{1}{3}=0.\overline{9}$$

當你進入無窮大的世界，什麼奇怪的事都會發生，這也是數學之所以迷人的原因之一。

換句話說，如果將有限思惟，用於無限的世界，將導致荒唐的結果。

舉個例子來說吧，我們學過一些有限級數的和，例如 $$1+2+3+4+\cdots+n=\frac{n(n+1)}{2}$$

如果加了無窮項之後，其值應該是無窮大，我們稱其為發散。也就是說 $$\sum_{n=1}^{\infty}n = \infty$$

可是如果你沒有注意到一些條件細節，將會得到以下這個離譜的結果：$$1+2+3+\cdots = \frac{-1}{12} \ \ (誤)$$ 等一會兒再回來看發生了什麼事。

高三時，我們已經知道，一個無窮等比級數收斂的條件為 $|公比|<1$，其收斂值為 $$S=\frac{首項}{1-公比}$$

例如 $$\sum_{n=0}^{\infty}\frac{1}{2^n}=\frac{1}{1-\frac{1}{2}}=2$$ 要注意，不是「近似 $2$」，而是「等於 $2$」

但是如果你沒考慮收斂條件，只是將公式背起來將結果套進去會如何？

答案是：荒唐的結果 $$1+2+4+\cdots+2^k+…=\frac{1}{1-2}=-1 \ \ (誤)$$

或是$$1-1+1-1+\cdots=\frac{1}{1-(-1)}=\frac{1}{2} \ \ (誤)$$

換句話說，確認無窮級數收斂的條件非常重要！

另外很多時候，同學很容易將「數列收斂」與「級數收斂」混洧。例如，考慮一個無窮數列 $<a_n>$ $$若 \sum_{n=1}^{\infty}a_n 收斂，則 \lim_{n\to\infty}a_n=0 $$ 反之不真。

換句話說，數列收斂，不保證級數收斂；但是級數收斂，可保證數列不僅收斂，而且收斂至 0。

有一個常見的例子，就是調和級數 $$\sum_{n=1}^{\infty}\frac{1}{n}=\infty$$ 但是 $$\lim_{n\to\infty}\frac{1}{n}=0$$

這個數列收斂至 $0$ 沒有問題。但是如何證明此級數發散呢？我們可以以分母的「位數」來分類比較：

分母是一位數，那麼每一項都會大於 $\frac{1}{10}$，即$$1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{9}>\frac{9}{10}$$
分母是二位數，那麼每一項都會大於 $\frac{1}{100}$，則$$\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\cdots+\frac{1}{99}>\frac{90}{100}=\frac{9}{10}$$
分母是三位數，那麼每一項都會大於 $\frac{1}{1000}$，則$$\frac{1}{100}+\frac{1}{101}+\frac{1}{102}+\cdots+\frac{1}{999}>\frac{900}{1000}=\frac{9}{10}$$
分母是四位數，那麼每一項都會大於 $\frac{1}{10000}$，則$$\frac{1}{1000}+\frac{1}{1001}+\frac{1}{1002}+\cdots+\frac{1}{9999}>\frac{9000}{10000}=\frac{9}{10}$$ 因此 $$\sum_{n=1}^{\infty}\frac{1}{n}\geq \frac{9}{10}+\frac{9}{10}+\frac{9}{10}+\frac{9}{10}+\cdots = \infty$$

這個在很多的教科書裡面都有寫。

但是，如果在此級數中移走任何包含 9 的數，則此級數 $S$ 會收斂或仍然發散呢？這個問題似乎很少出現在教科書中。

答案是：會收斂！

同樣以分母的位數來分類

分母為一位數的情形：$$1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{8}<8$$
分母為二位數的情形：$$\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\cdots+\frac{1}{88}<\frac{1}{10}\times (8\times 9) = 8\times\frac{9}{10}$$
分母為三位數的情形：$$\frac{1}{100}+\frac{1}{101}+\frac{1}{102}+…+\frac{1}{888}<\frac{1}{100}\cdot(8\times 9^2)=8\cdot(\frac{9}{10})^2$$

依此類推…

因此 $$級數 S \leq 8 [1+\frac{9}{10}+(\frac{9}{10})^2+\cdots]=8\cdot\frac{1}{1-\frac{9}{10}}=80$$

關於無窮級數在機率上的應用

擲2粒公正的骰子，直到其點數和為 6 或 7 點為止。
若點數和為 6 點比點數和為 7 點先出現，算你贏，否則算你輸。
那麼你獲勝的機率是多少？

已知，點數和為 6 點的可能性有 5 種，點數和為 7 點的可能性有 6 種。
那麼直覺上，可決定輸贏的有效點數和有 11 種，
其中有 5 種情況算你贏，有 6 種情況算你輸，那麼你贏的機率為 $\frac{5}{11}$。

這樣想是不是很籠統又抽象？

我們應該儘可能講清楚，
第一次擲骰子即獲勝的機率為 $\frac{5}{36}$

第二次擲骰子才獲勝的機率為多少？
那麼第一次擲骰子無法確定輸贏，機率為 $\frac{25}{36}$，第二次出現點數和為 6 點，
此時你獲勝的機率為 $\frac{25}{36}\times\frac{5}{36}$

第三次擲骰子才獲勝的機率為多少？
前兩次擲骰子無法確定輸贏，機率為 $(\frac{25}{36})^2$，第第三次出現點數和為 6 點，
此時你獲勝的機率為 $(\frac{25}{36})^2\times\frac{5}{36}$

一直下去，不知道哪一次才會贏，所以要將這些情形全部加起來，形成一個無窮等比級數：
$$\begin{aligned}
P(獲勝的機率) &= \frac{5}{36}+\frac{25}{36}\times\frac{5}{36}+(\frac{25}{36})^2\times\frac{5}{36}+\cdots \\
&= \frac{5}{36}\times [1+\frac{25}{36}+(\frac{25}{36})^2+\cdots] \\
&= \frac{5}{36}\times \frac{1}{1-\frac{25}{36}}\\
&= \frac{5}{36}\times \frac{36}{11} = \frac{5}{11}
\end{aligned}$$

違背直觀的現象：無窮級數重排後，可能導致不同結果

在有限的世界裡，將數列裡的數字重排，相加後的總和是不變的。

然而在無窮的世界裡，重排是會出問題的。

有一個例子是，$$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots = \sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}=ln2$$ 還記得這個級數的收斂值是如何計算出來的嗎？

再來複習一下：

考慮一個公比為 $-x$ 的幾何級數：$$1-x+x^2-x^3+…+(-x)^n+\cdots = \frac{1}{1+x}$$
將此式子積分：$$\int_0^1 1-t+t^2-t^3+…+(-t)^n+\cdots dt = \int_0^1 \frac{1}{1+t}dt $$ 因此可得 $$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots =ln2$$ 可是，如果將此級數重排會發生什麼事呢？
$$\begin{aligned}
級數 &= 1-\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{6}-\frac{1}{8}+\frac{1}{5}-\frac{1}{10}-\frac{1}{12}+\cdots \\
&= (1-\frac{1}{2})-\frac{1}{4}+(\frac{1}{3}-\frac{1}{6})-\frac{1}{8}+(\frac{1}{5}-\frac{1}{10})-\frac{1}{12}+\cdots \\
&= \frac{1}{2}-\frac{1}{4}+\frac{1}{6}-\frac{1}{8}+\frac{1}{10}-\frac{1}{12}+\cdots \\
&= \frac{1}{2}\cdot (1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots) \\
&= \frac{1}{2}ln2
\end{aligned}$$ 重排後的值竟然只有原級數的一半！

原因是，無限多個數相加，加法的交換律會失效！

如果想要重排後不改變其值，是有附加條件的，這裡先不談。

回到一開始的問題，為什麼會得到以下這個荒謬的結果？$$1+2+3+\cdots = \frac{-1}{12} \ \ (誤)$$

荒謬的結果，始於一連串的錯誤，我們使用「推移法」來推導：$$1-1+1-1+1-1+…=\frac{1}{2} \ \ (誤)$$ 推導過程如下：

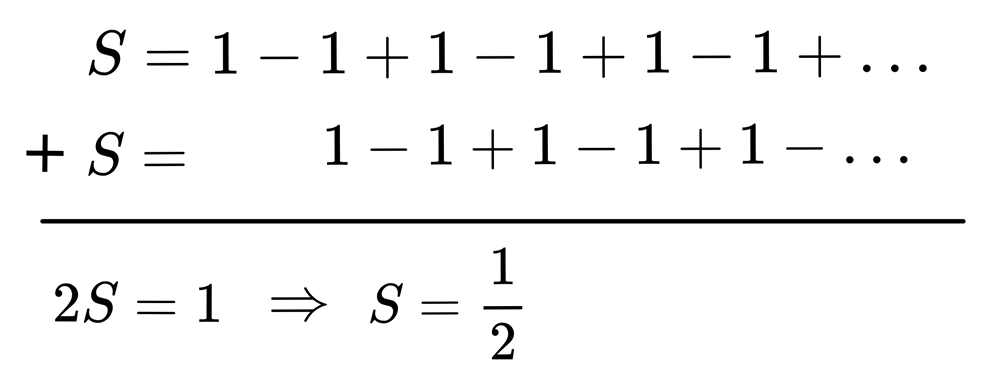
接著計算 $$1-2+3-4+5-6+7-8+\cdots=\frac{1}{4} \ \ (誤)$$ 推導過程如下：

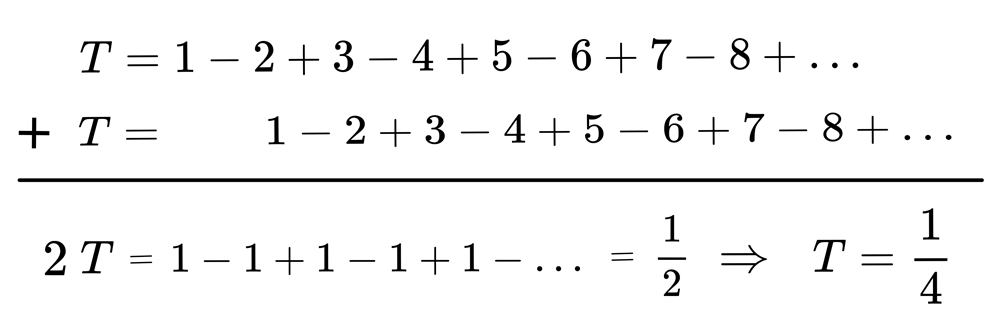
接著證明：$$V=1+2+3+4+5+6+\cdots=-\frac{1}{12}\ \ (誤)$$ 推導過程如下：

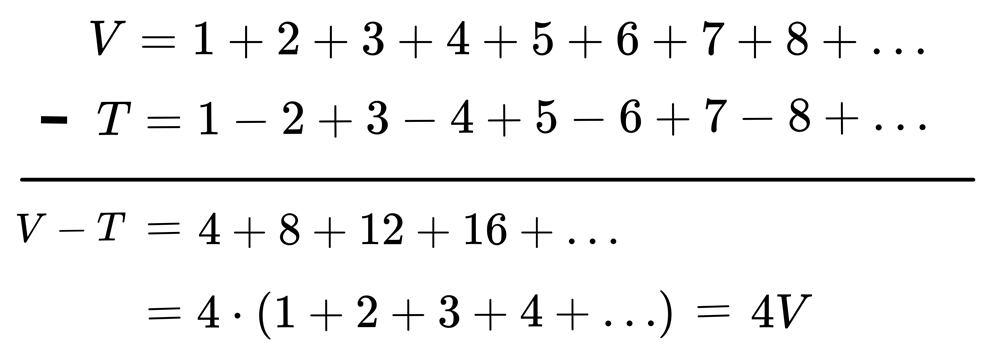
移項整理可得：$$V=-\frac{T}{3}=-\frac{1}{12}$$

關於有理數與無理數

課堂上，我們已經介紹了有理數與無理數的性質，它們都具有稠密性。

換句話說，有理數與無理數會緊密地排在數線上。

就以數量而言，它們都有無限多個。

然而，無理數比有理數多得多。

也就是說，如果我們在數線上隨便取一個數，這個數是無理數的機率大很多。

如何判斷其個數有如此大的差異呢？

有一個判斷指標就是，有理數有可數多個，無理數有不可數多個。

什麼是可數多個？

就是，可以與自然數一一對應的意思。

很明顯地，整數是可數的，我們可以排序如下：$$0, 1, -1, 2, -2, 3, -3, …$$
正的有理數可排序如下：$$\frac{1}{1}, \frac{1}{2}, \frac{2}{1}, \frac{1}{3}, \frac{2}{2}, \frac{3}{1}, \frac{1}{4}, \frac{2}{3}, \frac{3}{2}, \frac{4}{1}, \cdots$$
我們可以將 0 與負有理數穿插進去：$$0, \frac{1}{1}, -\frac{1}{1}, \frac{1}{2}, -\frac{1}{2}, \frac{2}{1}, -\frac{1}{2}, \frac{1}{3}, – \frac{1}{3}, \frac{2}{2}, – \frac{2}{2}, \frac{3}{1}, – \frac{3}{1}$$ 由左至右與正整數一一對應。

無理數有不可數多個，這件事是由德過數學家Cantor(1845~1918)證明，想法大致是這樣子：
如果無理數是可數多個，例如可以排序如下：
$$\begin{aligned}
0.347854156… \\
0.547614756…\\
0.457467417…\\
0.579231474…
\end{aligned}$$ 我們可以造一個小數 $0.r_1r_2r_3r_4…$，其中 $r_1\neq 3, r_2\neq 4, r_3\neq 7, r_4\neq 2,…$，

也就是說，
這個數的小數點後第1個數不可能為以上這些數中，第1個數的小數點後第1個數；
這個數的小數點後第2個數不可能為以上這些數中，第2個數的小數點後第2個數；
這個數的小數點後第3個數不可能為以上這些數中，第3個數的小數點後第3個數；
依此類推…

例如：$0.2561…$ 不可能出現在列表中。

這樣的做法就是Cantor的對角論證法，或稱為反例證法。

由以上討論，我們便可知道，同樣是無窮，但會有程度上的差異。

就很像，同樣是好學校的學生，也是會有程度的差異對吧？

這篇文章就先寫到這邊，祝學習愉快。

如果你對數學學習相關有興趣，可以留下你的姓名與e-mail訂閱電子報，獲得學習的相關資訊。