最近我在國中的課堂上,正在進行基礎整數論的教學:「如何求出兩正整數的最大公因數?」
一般來說,有三種方法:短除法、標準分解式找共同質因數中次方較低者、輾轉相除法。
前兩種方法還好解釋,第三種方法就不是三言兩語可以說清楚的。
優秀的學生不會滿足於技術操作,而是會想知道原理。
那麼我們就來談談輾轉相除法是怎麼來的。
首先,要從除法原理談起:任給兩個正整數 a、b,則存在唯一一組整數 q、r 滿足 a=bq+r 其中 0\leq r<b
那麼 a 與 b 的最大公因數等於 b 與 r 的最大公因數: (a,b)=(b,r) 這就是操作輾轉相除法的核心概念。
可是為什麼這是對的呢?
如果 r=0,則 a 是 b 的倍數,即 (a,b)=b=(b,r) 顯然成立。
因此,我們要聚焦在 r>0 的情況下,為何這個等式是對的呢?
首先,可以設 (a,b)=d_1、(b,r)=d_2
因為 d_1 是 a、b 的最大公因數,所以 d_1 必定是 a-bq 的因式(稍微想一下,不難)。
為了方便說明起見,以符號表示:d_1|a, d_1|b \Longrightarrow d_1|a-bq = r
因為 d_1|b, d_1|r 所以 d_1|(b,r)=d_2 故 d_1\leq d_2\tag{1}
另一方面,由 (b,r)=d_2 可知 d_2|b, d_2|r 則 d_2|bq+r = a
因為 d_2|a, d_2|b,所以d_2|(a,b)=d_1 故 d_2|d_1\tag{2}
由 (1)、(2) 可知 d_1=d_2 得證。
輾轉相除法就是反覆進行這樣的過程:
設 b_1、b_2 為正整數,且b_1>b_2,則存在整數 q,b_3 使得b_1=qb_2+b_3, \ 0\leq b_3<b_2
若 b_3=0,則 (b_1,b_2)=b_2
若 b_3>0,則存在整數 q_1, b_4 使得 b_2=q_1b_3+b_4, 0\leq b_4<b_3 即 (b_2, b_3)=(b_3,b_4)
一直持續這樣的過程,可以找到一個遞減數列 b_1>b_2>b_3>b_4>\cdots 滿足 (b_1,b_2)=(b_2,b_3)=\cdots=(b_i,b_{i+1}), i\in N
在有限步驟下,必定存在一個正整數 n 使得 b_{n+1}=0,此時 (b_1,b_2) = (b_n,b_{n+1}) = (b_n, 0) = b_n
此為歐幾里德算術(Euclid Algorithm),也是我們在課堂上帶同學操作的過程:
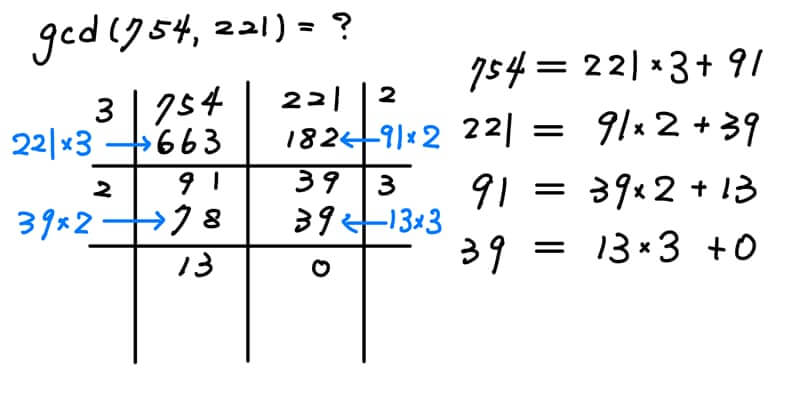
關於最大公因數的另一個觀點
透過上述的歐幾里德算術,我們可以知道,對於任意的整數 a、b,必定存在整數 s、t 滿足 sa+tb=gcd(a,b) \tag{*} 為什麼呢?
可以對於歐幾里德算術的步驟 n 進行數學歸納法
假設 a>b,n=1,也就是說一個步驟就結束了。
此時,存在一個整數 q 使得 a=bq,那麼 gcd(a,b)=b=1\cdot a+(b-a)=1\cdot a+(1-q)b 其中 s=1, t=1-q
接下來,假設 n<k 時,(*) 成立,則當 n=k,k>1 時會如何呢?
由除法原理可知,存在兩整數 q、r 滿足 a=bq+r, 0<r<b 由歸納法假設可知,存在整數 c、d 使得 cb+dr=gcd(b,r) 故 gcd(a,b)=gcd(b,r)=cb+dr=cb+d(a-bq)=da+(c-dq)b 令 s=d,t=c-dq 得證。
我們來做一個簡單的練習:如何找出整數 x、y 滿足 754x+221y=gcd(754,221)
同樣地,從歐幾里德算術開始:
\begin{aligned} 步驟1:754 &= 3\times 221+91 \\ 步驟2:221 &= 2\times 91+39 \\ 步驟3: \ 91 &= 2\times 39+13 \\ 步驟4: \ 39 &= 3\times 13 +0 \end{aligned} 因此可得 gcd(754,221)=13
接著將以上操作反過來寫:
\begin{aligned} 13 &= 91-2\times 39 \\ &= 91-2\times (221-2\times 91) \\ &= 5\times 91 -2\times 221 \\ &= 5\times (754-3\times 221)-2\times 221\\ &=5\times 754 – 17\times 221 \end{aligned} 找到了,x=5、y=-17
可是,如果考慮一般的整係數方程式 ax+by=c,要如何確定有整數解呢?
如果整係數方程式 ax+by=c 有整數解,則 (a,b) | ax+by,因此可得 (a,b) | c,
也就是說,(a,b)| c 是整係數方程式 ax+by=c 有整數解的必要條件。
另一方面,若 (a,b) | c,則存在一個整數 q 使得 c=(a,b)\times q
由以上討論可知,存在整數 s, t 使得 sa+tb=(a,b) 即(sq)a+(tq)b=(a,b)\cdot q=c 此時 x=sq,\ y=tq
但是還有個問題,這個整係數方程式 ax+by=c 應該不只一組解吧,那其他解要如何找呢?
很簡單,其實就是找出直線 ax+by=c 上的格子點(x、y 坐標皆為整數的點)。
假設,經由歐幾里德算術,我們可以找到一組解 (x_0, y_0),而且令 x, y 是另一組整數解,
則 \frac{y-y_0}{x-x_0}=-\frac{a}{b}=\frac{a/d}{-b/d} 其中 d=(a,b),因此
\begin{cases} x&= x_0-\frac{b}{d}k \\ y&= y_0+\frac{a}{d}k \end{cases}
看完以上介紹,請同學不妨試著做做看以下這道題:

自己先想過再看解法喔。
根據除法原理:
\begin{align} 629 &= 357\cdot 1 + 272 \\ 357 &= 272\cdot 1 + 85 \\ 272 &= 85\cdot 3 +17 \\ 85 &= 17\cdot 5 +0 \end{align}
將以上計算由後往前推:
\begin{aligned} 17 &= 272 -3\cdot 85 \\ &= 272-3\cdot (357-272\cdot 1) \\ &= 4\cdot 272 – 3\cdot 357 \\ &= 4\cdot (629-357) – 3\cdot 357 \\ &= -7\cdot 357 + 4\cdot 629 \end{aligned}
以上的計算過程,可以呈現如下:
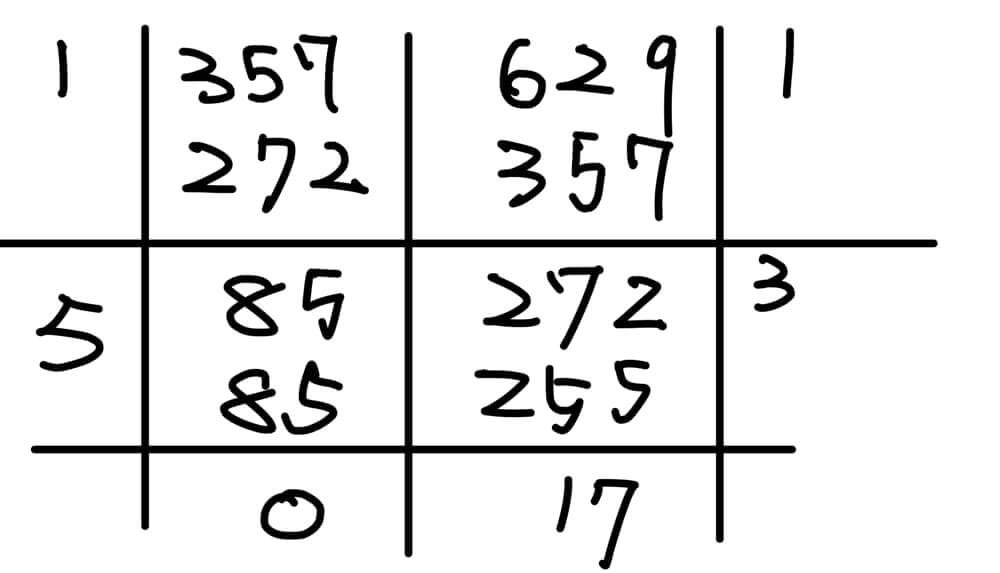
如果看得不是很清楚,不妨用符號來表示:令 a=357、b=629 則
\begin{aligned} b &= a\cdot 1 + (b-a) \\ a &= (b-a) \cdot 1 + (2a-b) \\ (b-a) &= (2a-b)\cdot 3 + (-7a+4b) \\ (2a-b) &= (-7a+4b)\cdot 5 + 0 \end{aligned} 因此,-7a+4b=17 圖示如下:

第(2)題的部份:[357, 629] = \frac{357\times 629}{(357, 629)}=\frac{357\times 629}{17} = 13209
這篇文章就先寫到這邊,提供給學生們當作課外補充參考。
最後也放一部Youtube優質影片給大家參考







(舉手)為什麼最近都沒有新的文章?
同學電腦課下課都在看這個網站:)
還在寫喔,請耐心等候,呵呵 😀
期待~~~
好喔!
阿朗最近過得可好?