大部份有趣的數學都不是寫在教科書裡
為此,我鼓勵學生多讀課外書,會發現截然不同的數學世界。
這一篇文章,我要來探討「無窮」這個讓學生感到新奇的概念。
請注意,無窮是概念,而不是數字。
一個常見的例子,\(0.\overline{9}\) 與 \(1\) 哪個數字較大?
大多數學生會回答,\(1\) 比較大,極少數學生會回答一樣大,還有幾位調皮搗蛋的會說 \(0.\overline{9}\) 比較大。
簡單來說,因為 \(\frac{1}{3}=0.\overline{3}\),所以 $$1=3\times \frac{1}{3}=0.\overline{9}$$
當你進入無窮大的世界,什麼奇怪的事都會發生,這也是數學之所以迷人的原因之一。
換句話說,如果將有限思惟,用於無限的世界,將導致荒唐的結果。
舉個例子來說吧,我們學過一些有限級數的和,例如 $$1+2+3+4+\cdots+n=\frac{n(n+1)}{2}$$
如果加了無窮項之後,其值應該是無窮大,我們稱其為發散。也就是說 $$\sum_{n=1}^{\infty}n = \infty$$
可是如果你沒有注意到一些條件細節,將會得到以下這個離譜的結果:$$1+2+3+\cdots = \frac{-1}{12} \ \ (誤)$$ 等一會兒再回來看發生了什麼事。
高三時,我們已經知道,一個無窮等比級數收斂的條件為 \(|公比|<1\),其收斂值為 $$S=\frac{首項}{1-公比}$$
例如 $$\sum_{n=0}^{\infty}\frac{1}{2^n}=\frac{1}{1-\frac{1}{2}}=2$$ 要注意,不是「近似 \(2\)」,而是「等於 \(2\)」
但是如果你沒考慮收斂條件,只是將公式背起來將結果套進去會如何?
答案是:荒唐的結果 $$1+2+4+\cdots+2^k+…=\frac{1}{1-2}=-1 \ \ (誤)$$
或是$$1-1+1-1+\cdots=\frac{1}{1-(-1)}=\frac{1}{2} \ \ (誤)$$
換句話說,確認無窮級數收斂的條件非常重要!
另外很多時候,同學很容易將「數列收斂」與「級數收斂」混洧。例如,考慮一個無窮數列 \(<a_n>\) $$若 \sum_{n=1}^{\infty}a_n 收斂,則 \lim_{n\to\infty}a_n=0 $$ 反之不真。
換句話說,數列收斂,不保證級數收斂;但是級數收斂,可保證數列不僅收斂,而且收斂至 0。
有一個常見的例子,就是調和級數 $$\sum_{n=1}^{\infty}\frac{1}{n}=\infty$$ 但是 $$\lim_{n\to\infty}\frac{1}{n}=0$$
這個數列收斂至 \(0\) 沒有問題。但是如何證明此級數發散呢?我們可以以分母的「位數」來分類比較:
分母是一位數,那麼每一項都會大於 \(\frac{1}{10}\),即$$1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{9}>\frac{9}{10}$$
分母是二位數,那麼每一項都會大於 \(\frac{1}{100}\),則$$\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\cdots+\frac{1}{99}>\frac{90}{100}=\frac{9}{10}$$
分母是三位數,那麼每一項都會大於 \(\frac{1}{1000}\),則$$\frac{1}{100}+\frac{1}{101}+\frac{1}{102}+\cdots+\frac{1}{999}>\frac{900}{1000}=\frac{9}{10}$$
分母是四位數,那麼每一項都會大於 \(\frac{1}{10000}\),則$$\frac{1}{1000}+\frac{1}{1001}+\frac{1}{1002}+\cdots+\frac{1}{9999}>\frac{9000}{10000}=\frac{9}{10}$$ 因此 $$\sum_{n=1}^{\infty}\frac{1}{n}\geq \frac{9}{10}+\frac{9}{10}+\frac{9}{10}+\frac{9}{10}+\cdots = \infty$$
這個在很多的教科書裡面都有寫。
但是,如果在此級數中移走任何包含 9 的數,則此級數 \(S\) 會收斂或仍然發散呢?這個問題似乎很少出現在教科書中。
答案是:會收斂!
同樣以分母的位數來分類
分母為一位數的情形:$$1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{8}<8$$
分母為二位數的情形:$$\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\cdots+\frac{1}{88}<\frac{1}{10}\times (8\times 9) = 8\times\frac{9}{10}$$
分母為三位數的情形:$$\frac{1}{100}+\frac{1}{101}+\frac{1}{102}+…+\frac{1}{888}<\frac{1}{100}\cdot(8\times 9^2)=8\cdot(\frac{9}{10})^2$$
依此類推…
因此 $$級數 S \leq 8 [1+\frac{9}{10}+(\frac{9}{10})^2+\cdots]=8\cdot\frac{1}{1-\frac{9}{10}}=80$$
關於無窮級數在機率上的應用
擲2粒公正的骰子,直到其點數和為 6 或 7 點為止。
若點數和為 6 點比點數和為 7 點先出現,算你贏,否則算你輸。
那麼你獲勝的機率是多少?
已知,點數和為 6 點的可能性有 5 種,點數和為 7 點的可能性有 6 種。
那麼直覺上,可決定輸贏的有效點數和有 11 種,
其中有 5 種情況算你贏,有 6 種情況算你輸,那麼你贏的機率為 \(\frac{5}{11}\)。
這樣想是不是很籠統又抽象?
我們應該儘可能講清楚,
第一次擲骰子即獲勝的機率為 \(\frac{5}{36}\)
第二次擲骰子才獲勝的機率為多少?
那麼第一次擲骰子無法確定輸贏,機率為 \(\frac{25}{36}\),第二次出現點數和為 6 點,
此時你獲勝的機率為 \(\frac{25}{36}\times\frac{5}{36}\)
第三次擲骰子才獲勝的機率為多少?
前兩次擲骰子無法確定輸贏,機率為 \((\frac{25}{36})^2\),第第三次出現點數和為 6 點,
此時你獲勝的機率為 \((\frac{25}{36})^2\times\frac{5}{36}\)
一直下去,不知道哪一次才會贏,所以要將這些情形全部加起來,形成一個無窮等比級數:
$$\begin{aligned}
P(獲勝的機率) &= \frac{5}{36}+\frac{25}{36}\times\frac{5}{36}+(\frac{25}{36})^2\times\frac{5}{36}+\cdots \\
&= \frac{5}{36}\times [1+\frac{25}{36}+(\frac{25}{36})^2+\cdots] \\
&= \frac{5}{36}\times \frac{1}{1-\frac{25}{36}}\\
&= \frac{5}{36}\times \frac{36}{11} = \frac{5}{11}
\end{aligned}$$
違背直觀的現象:無窮級數重排後,可能導致不同結果
在有限的世界裡,將數列裡的數字重排,相加後的總和是不變的。
然而在無窮的世界裡,重排是會出問題的。
有一個例子是,$$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots = \sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}=ln2$$ 還記得這個級數的收斂值是如何計算出來的嗎?
再來複習一下:
考慮一個公比為 \(-x\) 的幾何級數:$$1-x+x^2-x^3+…+(-x)^n+\cdots = \frac{1}{1+x}$$
將此式子積分:$$\int_0^1 1-t+t^2-t^3+…+(-t)^n+\cdots dt = \int_0^1 \frac{1}{1+t}dt $$ 因此可得 $$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots =ln2$$ 可是,如果將此級數重排會發生什麼事呢?
$$\begin{aligned}
級數 &= 1-\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{6}-\frac{1}{8}+\frac{1}{5}-\frac{1}{10}-\frac{1}{12}+\cdots \\
&= (1-\frac{1}{2})-\frac{1}{4}+(\frac{1}{3}-\frac{1}{6})-\frac{1}{8}+(\frac{1}{5}-\frac{1}{10})-\frac{1}{12}+\cdots \\
&= \frac{1}{2}-\frac{1}{4}+\frac{1}{6}-\frac{1}{8}+\frac{1}{10}-\frac{1}{12}+\cdots \\
&= \frac{1}{2}\cdot (1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots) \\
&= \frac{1}{2}ln2
\end{aligned}$$ 重排後的值竟然只有原級數的一半!
原因是,無限多個數相加,加法的交換律會失效!
如果想要重排後不改變其值,是有附加條件的,這裡先不談。
回到一開始的問題,為什麼會得到以下這個荒謬的結果?$$1+2+3+\cdots = \frac{-1}{12} \ \ (誤)$$
荒謬的結果,始於一連串的錯誤,我們使用「推移法」來推導:$$1-1+1-1+1-1+…=\frac{1}{2} \ \ (誤)$$ 推導過程如下:

接著計算 $$1-2+3-4+5-6+7-8+\cdots=\frac{1}{4} \ \ (誤)$$ 推導過程如下:
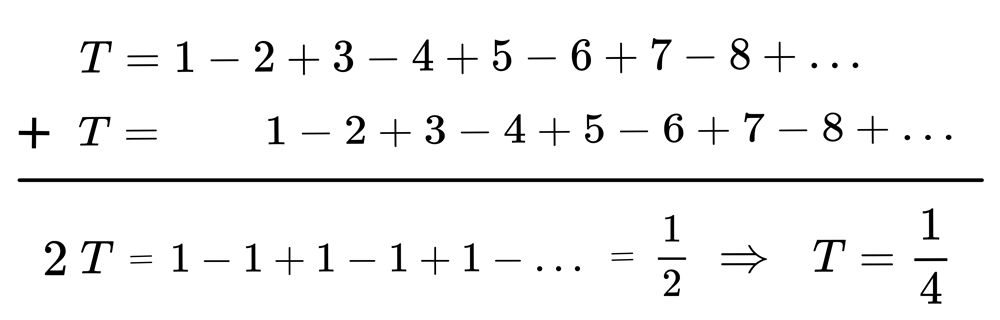
接著證明:$$V=1+2+3+4+5+6+\cdots=-\frac{1}{12}\ \ (誤)$$ 推導過程如下:

移項整理可得:$$V=-\frac{T}{3}=-\frac{1}{12}$$
關於有理數與無理數
課堂上,我們已經介紹了有理數與無理數的性質,它們都具有稠密性。
換句話說,有理數與無理數會緊密地排在數線上。
就以數量而言,它們都有無限多個。
然而,無理數比有理數多得多。
也就是說,如果我們在數線上隨便取一個數,這個數是無理數的機率大很多。
如何判斷其個數有如此大的差異呢?
有一個判斷指標就是,有理數有可數多個,無理數有不可數多個。
什麼是可數多個?
就是,可以與自然數一一對應的意思。
很明顯地,整數是可數的,我們可以排序如下:$$0, 1, -1, 2, -2, 3, -3, …$$
正的有理數可排序如下:$$\frac{1}{1}, \frac{1}{2}, \frac{2}{1}, \frac{1}{3}, \frac{2}{2}, \frac{3}{1}, \frac{1}{4}, \frac{2}{3}, \frac{3}{2}, \frac{4}{1}, \cdots$$
我們可以將 0 與 負有理數穿插進去:$$0, \frac{1}{1}, -\frac{1}{1}, \frac{1}{2}, -\frac{1}{2}, \frac{2}{1}, -\frac{1}{2}, \frac{1}{3}, – \frac{1}{3}, \frac{2}{2}, – \frac{2}{2}, \frac{3}{1}, – \frac{3}{1}$$ 由左至右與正整數一一對應。
無理數有不可數多個,這件事是由德過數學家Cantor(1845~1918)證明,想法大致是這樣子:
如果無理數是可數多個,例如可以排序如下:
$$\begin{aligned}
0.347854156… \\
0.547614756…\\
0.457467417…\\
0.579231474…
\end{aligned}$$ 我們可以造一個小數 \(0.r_1r_2r_3r_4…\),其中 \(r_1\neq 3, r_2\neq 4, r_3\neq 7, r_4\neq 2,…\),
也就是說,
這個數的小數點後第1個數不可能為以上這些數中,第1個數的小數點後第1個數;
這個數的小數點後第2個數不可能為以上這些數中,第2個數的小數點後第2個數;
這個數的小數點後第3個數不可能為以上這些數中,第3個數的小數點後第3個數;
依此類推…
例如:\(0.2561…\) 不可能出現在列表中。
這樣的做法就是Cantor的對角論證法,或稱為反例證法。
由以上討論,我們便可知道,同樣是無窮,但會有程度上的差異。
就很像,同樣是好學校的學生,也是會有程度的差異對吧?
這篇文章就先寫到這邊,祝學習愉快。
如果你對數學學習相關有興趣,可以留下你的姓名與e-mail訂閱電子報,獲得學習的相關資訊。

歡迎訂閱 高中數學數位學習電子報