在高中數學的數列章節中,我們習慣了等差、等比這些規律整齊的數列。
但在數學競賽或更高等的動力系統理論中,有一類數列是「自己生成自己」的。
這週我們要探討的題目看似簡單,只有小學程度的乘法,
但它背後卻隱藏著「有限狀態機」與「鴿籠原理」的深刻數學結構。
讓我們一起來看這道如同生物細胞分裂般的有趣題目。

一、 題目拆解:追蹤數字的生長軌跡
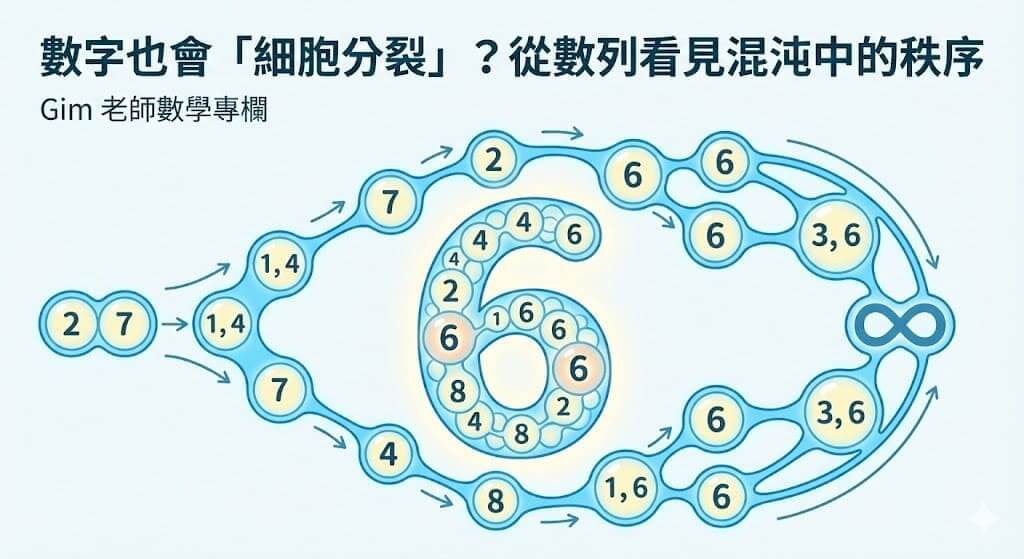
題目給定一個數列,起始項為 \( 2, 7 \)。
生成規則如下:將「相鄰的前兩項」相乘。
- 如果乘積是 一位數,則直接作為下一項。
- 如果乘積是 二位數,則將其十位數與個位數依序作為下兩項。
我們的目標是:證明數字 6 在此數列中出現無窮多次。
這個規則意味著數列的長度會不斷增長,而且增長的速度取決於我們算出多少個「二位數」。
這就像是一個動態的系統,前面的基因(數字)決定了後面的樣貌。
二、 實驗階段:讓數列「跑」起來
在進入嚴謹證明之前,我們必須先動手計算,培養對這個數列的「數感」。
讓我們像偵探一樣,一步步追蹤生成的過程。
令數列為 \( a_n \)。
初始狀態:
\[ 2, 7 \]
第 1 步: 考慮第 1、2 項 \( 2 \times 7 = 14 \)。
因為是二位數,補上 \( 1, 4 \)。
數列變為:
\[ 2, 7, \mathbf{1, 4} \]
第 2 步: 考慮第 2、3 項(指標向後移)\( 7 \times 1 = 7 \)。
是一位數,補上 \( 7 \)。
數列變為:
\[ 2, 7, 1, 4, \mathbf{7} \]
第 3 步: 考慮第 3、4 項 \( 1 \times 4 = 4 \)。
是一位數,補上 \( 4 \)。
數列變為:
\[ 2, 7, 1, 4, 7, \mathbf{4} \]
第 4 步: 考慮第 4、5 項 \( 4 \times 7 = 28 \)。
是二位數,補上 \( 2, 8 \)。
數列變為:
\[ 2, 7, 1, 4, 7, 4, \mathbf{2, 8} \]
第 5 步: 考慮第 5、6 項 \( 7 \times 4 = 28 \)。
補上 \( 2, 8 \)。
數列變為:
\[ \dots, 7, 4, 2, 8, \mathbf{2, 8} \]
第 6 步: 考慮第 6、7 項 \( 4 \times 2 = 8 \)。
補上 \( 8 \)。
數列變為:
\[ \dots, 2, 8, 2, 8, \mathbf{8} \]
第 7 步: 考慮第 7、8 項 \( 2 \times 8 = 16 \)。
是二位數,補上 \( 1, 6 \)。
數列變為:
\[ \dots, 2, 8, 2, 8, 8, \mathbf{1, 6} \]
看見了嗎? 在第 7 步的運算中,數字 6 終於誕生了!
目前的數列尾端是 \( \dots, 1, 6 \)。
這只證明了 6 出現了「一次」,如何證明它會出現「無窮多次」?
三、 數學結構分析:鴿籠原理與循環
要證明無窮多次,我們不需要算出無窮多項,
而是要證明這個系統會進入一個包含 6 的「死循環」。
1. 有限狀態機的概念
這個數列的每一項 \( a_k \),完全由它前面的兩項 \( a_{k-1}, a_{k-2} \) 的乘積決定
因為每一項都是 \( 0 \) 到 \( 9 \) 的整數,
所以任意相鄰兩項的組合 \( (x, y) \) 只有有限種可能。
具體來說,最多只有 \( 10 \times 10 = 100 \) 種組合。
2. 必然發生的循環
根據 鴿籠原理 (Pigeonhole Principle),當我們不斷生成新的項,
遲早會遇到一對「曾經出現過」的相鄰數字組合。
一旦某個組合 \( (x, y) \) 再次出現,根據確定的乘法規則,
它產生的下一項(或兩項)也會完全相同,接下來的發展就會完全複製之前的歷史。
這意味著:此數列最終必將進入週期性的循環。
3. 驗證 6 在循環中
我們已經發現了數字 6 的出現。讓我們檢查 6 是否有能力「繁衍」自己。
在第 7 步我們得到了 \( 1, 6 \)。
當生成指針移動到這對 \( 1, 6 \) 時:
\[ 1 \times 6 = 6 \]
這會產生一個新的 \( 6 \)。
如果未來出現 \( 6, 6 \) 的組合:
\[ 6 \times 6 = 36 \]
這會產生 \( 3, 6 \),依然帶有 6。
由於數列必定進入循環,且我們已經觀察到 6 透過 \( 2 \times 8 = 16 \) 被製造出來,
並且 6 參與運算後(如 \( 1 \times 6 \))能再次生成 6。
只要這個循環不全是 \( 0 \)(顯然不可能,因為我們一直在生成非零數),
數字 6 就會隨著循環不斷重複出現。
因此,證得數字 6 在此數列中出現無窮多次。
四、 課後解題註解:高中數學的連結
這道題目雖然形式新穎,但其核心觀念緊扣高中數學的幾個重要章節:
- 數列與級數 (Sequence and Series):
訓練觀察數列規律與遞迴關係 (Recurrence Relation) 的能力。這是一種特殊的非線性遞迴。 - 排列組合 (Permutation and Combination):
運用「鴿籠原理」來證明在有限狀態下,重複情形必然發生。這是處理「存在性證明」的強力工具。 - 邏輯推理 (Logical Reasoning): 從特例觀察(歸納)到結構證明(演繹)的完整數學思維過程。
Gim 老師的學習建議:
下次遇到這種「操作型」的數列問題,不要害怕列舉。
先算出前幾項,往往規律就在你的筆尖下浮現。
數學的直觀,建立在紮實的動手實驗之上。