
免費訂閱 高中數學數位學習電子報
訂閱電子報,加入數學科普書籍、文章閱讀計畫
你是否還記得,我之前寫的一篇文章,標題為「從最美的數學公式找尋數學發展的脈絡」,
這個最美的公式就是 $$e^{i\pi}+1=0$$ 串連了五個非常重要的常數 \(0, 1, i, \pi, e\)。
每個常數都有各自豐富的故事,其中圓周率 \(\pi\) 是我認為最不簡單的。
圓周率,顧名思義,就是與「圓」相關的常數,
國小時,老師說這個數是 \(3.14\),上了國中後,老師說不能寫成 \(3.14\),應該要用符號 \(\pi\) 來表示。
\(\pi\) 與 \(\sqrt{2}\)、\(e\) 同樣都是無理數,我們日前也已證明後兩者。
然而,\(\pi\) 是無理數的證明困難許多,
一直到 1761 年,才由數學家朗伯(Johann Heinrich Lambert)透過連分數證明出來。
另外,與 \(\sqrt{2}\) 這種無理數還有一個本質上的差異:\(\pi\) 是一個「超越數」。
什麼是超越數呢?
就是它不是任何整係數多項式方程式的根。
與之相對的稱為「代數數」,必定為某個整係數方程式的根。
顯然 \(\sqrt{2}\) 是方程式 \(x^2-2=0\) 的一根,因此它是一個代數數。
想要對圓周率有比較清楚的了解,則必須藉助微積分將其量化。
因此這篇文章,我們會開始觸及到一些高等數學的內容。
開始吧!
圓周率 \(\pi\) 是如何被發現的?
你可以拿一個圓柱形的杯子,然後再拿一條繩子將杯子繞一圈。

接著拿出你的尺,量一下這個圓圈的直徑 \(D\) 以及用到的繩長 \(C\)。
過程中一定會有誤差,沒關係。
接著將這兩個數據相除,你會發現這個比值大約是 \(3.14\):$$\frac{C}{D}\approx 3.14$$
無論你拿哪一個圓柱形的杯子,用此方式測量,會發現這個比值是一樣(或接近)的。
這個比值就是我們說的圓周率。
至此,我們對於圓周率的理解還是非常粗淺。
你還記不記得,我們在課堂上朗朗上口的圓面積、圓周長公式:$$圓面積=\pi\cdot r^2, \ 圓周長=2\pi\cdot r$$
到了高中第四冊,講到空間概念的時候,還會提到球的體積及表面積公式:$$球體積=\frac{4}{3}\pi r^3,\ 球表面積=4\pi r^2$$
但是你有想過為什麼嗎?
當然,用微積分就可以輕易推導出來,這是最嚴謹的方法,牛頓與萊布尼茲的發明真偉大。
但是我們也可以用比較直觀的方法進一步理解:切匹薩
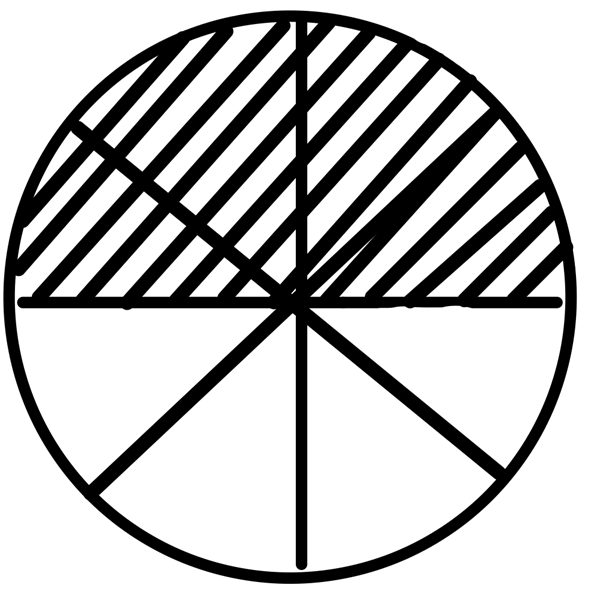
我們將這個圓切成八等份後,重新排列如下:
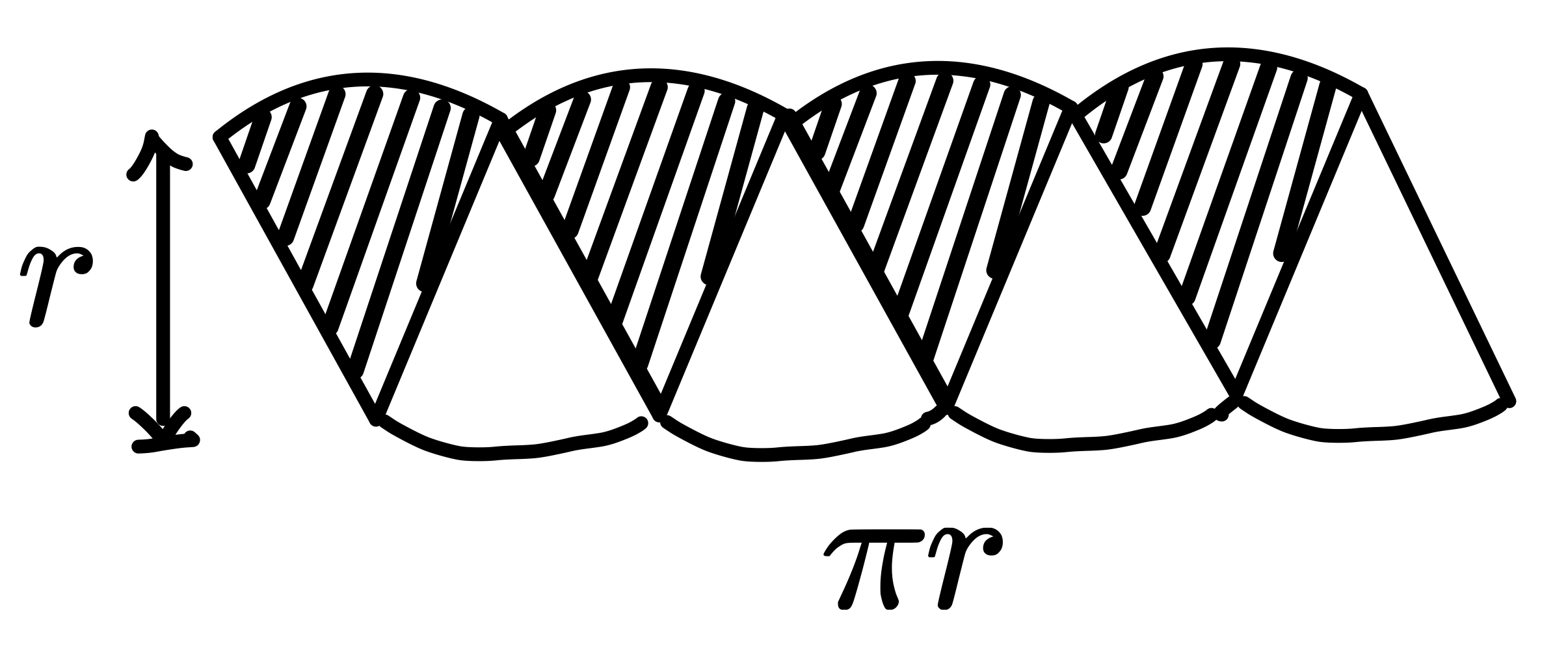
是不是看起來有點像平行四邊形,如果我們已經知道圓周長為 \(2\pi\times r\),
那麼這個看起來有點像平行四邊形的圖形面積很像 \(\pi r\times r = \pi\times r^2\)
這也差太多了吧?
沒關係,再切得更細一點,就會更像了
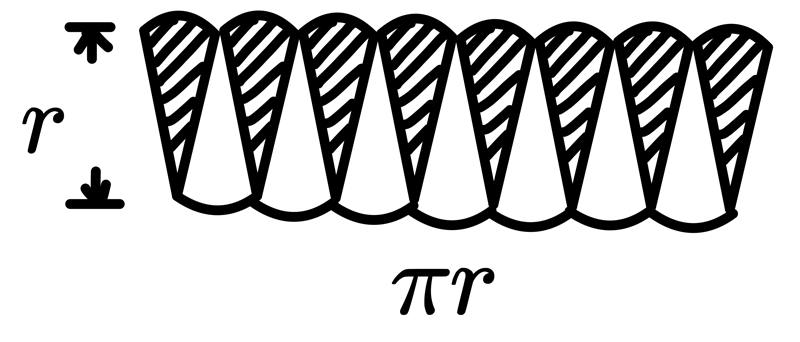
再繼續切,你有沒有發現,愈來愈像一個長為 \(\pi r\)、寬為 \(r\) 的長方形?
雖然這樣不嚴謹,但還挺好玩的。
你覺得還可以怎麼切?
剛剛是切匹薩,這次我們來切洋蔥(食物總是讓人比較有印象)
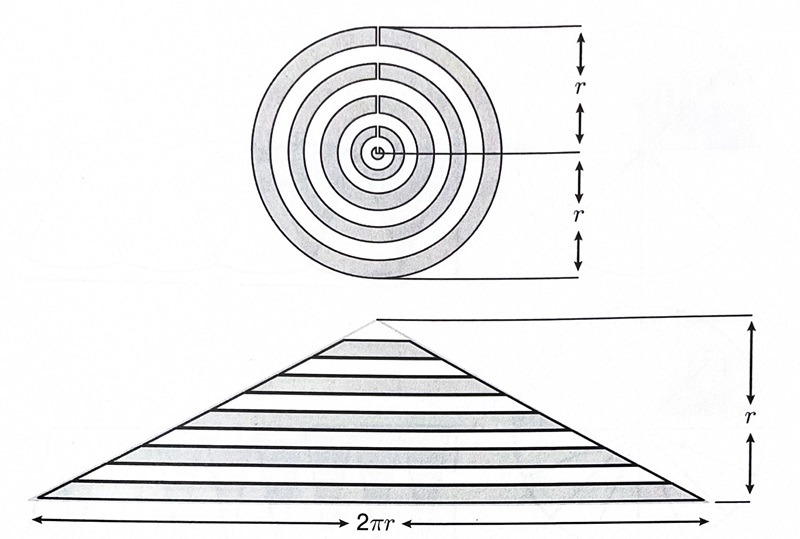
考慮一個有很多同心環且半徑為 \(r\) 的大圓,將這個大圓從中心點上方切開,然後將這些環全部拉直。
這可能須要你的一些想像力。
然後就可以排成一個看起來挺像是三角形的形狀。
這個三角形的底為 \(2\pi r\)、高為 \(r\),因此面積為 \(\pi r^2\)
但是我們無法確認這個三角形的兩邊是否為直線,因此還是存在誤差。
隨著愈切愈細,這個誤差就會愈來愈小。
好玩嗎?
國小老師曾經告訴我們,圓周率是 \(3.14\),這雖然不是一個精確的數字,
但是是怎麼冒出來的?
先來點開胃菜:要如何證明 \(3<\pi<4\)?
首先,考慮一個邊長為 \(2\) 的正方形,剛好可以包住半徑為 \(1\) 的圓,並且圓可以包住邊長為 \(1\) 的正六邊形:
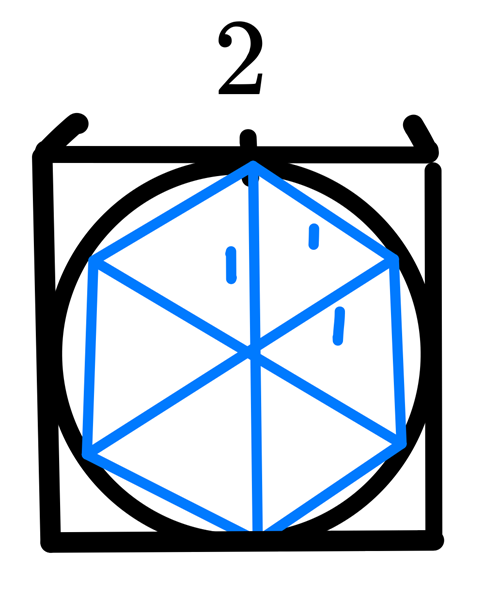
因此這個圓的面積小於正方形的面積:\(\pi\cdot 1^2 < 4\),周長大於正六邊形的周長:\(2\pi > 6\)
因此 $$ 3< \pi <4 $$
這是個很粗淺的估計
那麼如果將圓外切的正方形改成圓外切的正六邊形會如何呢?
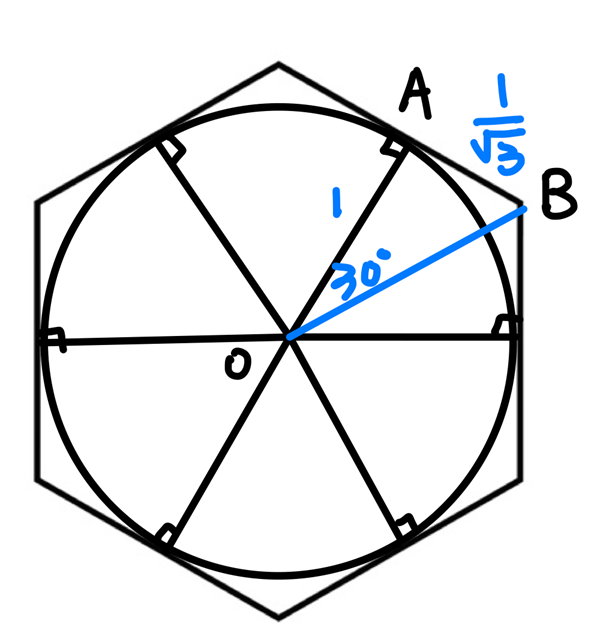
圓外切六邊形的面積=\(\Delta OAB\) 面積的 \(12\) 倍。因此 $$\frac{1}{2}\cdot 1\cdot\frac{1}{\sqrt{3}}\cdot 12 > \pi$$
因此我們可以得到更精準的估計:$$\pi < 2\sqrt{3}$$
按照這個方式,如果我們不斷做這個圓的內接和外切正多邊形,那麼估計是不是會更精準呢?
有位數學家,阿基米德就真的做了這件事:
他持續作 12、24、48、96 邊的內接和外切正多邊形,因此導出 $$3.14103 < \pi < 3.14271$$ 以及一個不等式:$$3\frac{10}{71}<\pi<3\frac{1}{7}$$
這真的需要無比的耐心。
耐心是學好數學的基本裝備,家長不妨觀察一下,喜歡數學的小孩通常都比較有耐心。
圓周率的故事,不是一篇小文章講得完的,之後的主題一定會持續與之關聯。
最後來複習一下基礎的微積分作為結束。
如何精準計算出圓的面積呢?
首先寫出圓心為 \(O\),半徑為 \(r\) 的圓方程式:\(x^2+y^2=r^2\)
接著,算出函數 \(y=\sqrt{r^2-x^2}\) 與 \(x\) 軸圍出的區域面積:
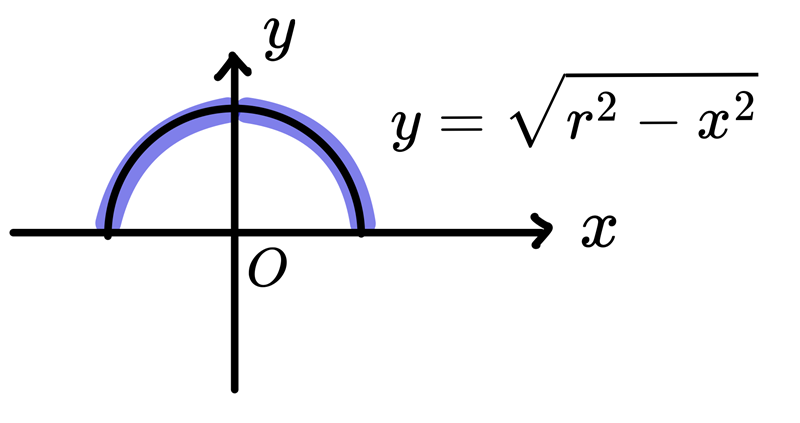
$$\begin{aligned}
圓面積 &= 2\int_{-r}^r \sqrt{r^2-x^2}dx \\
&=2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sqrt{r^2(1-sin^2\theta)}\cdot rcos\theta d\theta , \ \ \ \ (x=rsin\theta)\\
&=2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} r^2 cos^2\theta d\theta \\
&=2r^2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1+cos2\theta}{2}d\theta \\
&= r^2(\theta+\frac{1}{2}sin2\theta)|_{-\frac{\pi}{2}}^{\frac{\pi}{2}}=\pi r^2
\end{aligned}$$
這個公式在高中就會提到,因此推導過程先略過。
但是圓周長的部份,高中課本沒有特別提,公式的由來要先知道一下。
首先,先令 \(y=f(x)=\sqrt{r^2-x^2}\),並且將區間 \([-r,r]\) 作一個分割:$$\{-r=x_0, x_1, x_2, …, x_n=r\}$$
我們在每一個小區間裡求圓上兩點的連線段長:
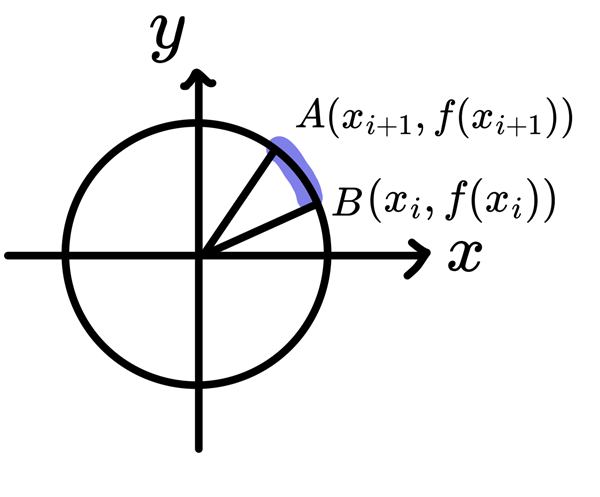
$$\begin{aligned}
\overline{AB} &= \sum_{i=0}^{n-1}\sqrt{(x_i-x_{i+1})^2+(f(x_i)-f(x_{i+1}))^2} \\
&= \sum_{i=0}^{n-1}\sqrt{1+(\frac{f(x_i)-f(x_{i+1}}{x_i-x_{i+1})})^2}(x_i-x_{i+1})
\end{aligned}$$
當然這樣算出來會有誤差,但隨著分割愈來愈細,誤差就會愈來愈小。
接著取極限:令 \(n\rightarrow\infty\) 可得
$$\begin{aligned}
圓周長 &= 2\int_{-r}^r \sqrt{1+f'(x)^2}dx \\
&=2\int_{-r}^r \sqrt{1+\frac{x^2}{r^2-x^2}}dx \\
&= 2\int_{-r}^r \frac{r}{\sqrt{r^2-x^2}}dx \\
&=2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{r}{rcos\theta}\cdot rcos\theta d\theta \ \ \ (令x=rsin\theta) \\
&=2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} r d\theta = 2\pi r
\end{aligned}$$
球體積的部份,則是要算旋轉體體積:
將函數 \(y=\sqrt{r^2-x^2}\) 繞著 \(x\) 軸旋轉一圈可得體積 \(V\)
$$\begin{aligned}
V &= \pi\int_{-r}^r (r^2-x^2) dx \\
&= \pi (r^2x-\frac{x^3}{3}) |_{-r}^r \\
&= \frac{4}{3}\pi r^3
\end{aligned}$$
最後,來看看球的表面積是如何計算出來的。
球是一種曲面,我們可以想像成切西瓜。
假設這個西瓜是完美的球形,而且切得非常薄,薄得像一個半徑為 \(r_i\) 的圓形:
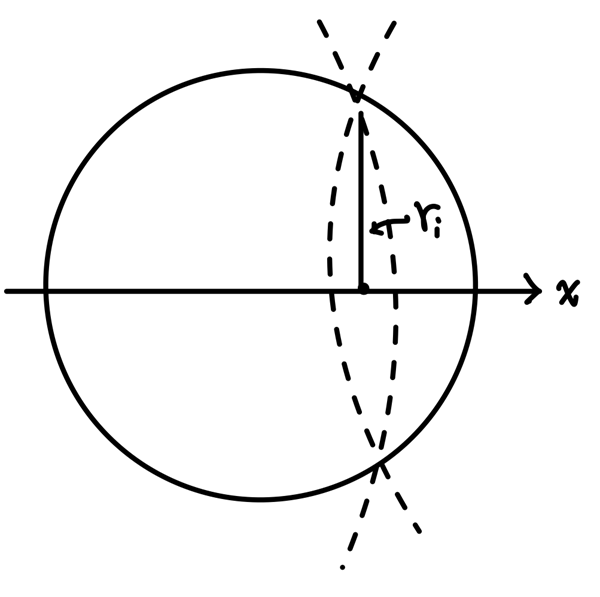
每個圓形的周長為 \(2\pi r_i\),其中 \(r_i=f(x_i)\)
接著將這些圓周長不間斷地一片片接起來,每一片的表面積為
$$2\pi r_i\sqrt{(\Delta x_i)^2+(\Delta y_i)^2} =2\pi r_i\sqrt{1+(\frac{\Delta y_i}{\Delta x_i})^2} \Delta x_i$$ 設 \(y=f(x)=\sqrt{r^2-x^2}\),則
$$\begin{aligned}
圓表面積&= \ \int_{-r}^r 2\pi f(x) \sqrt{1+f'(x)^2} dx \\
&= 2\pi \int_{-r}^r \sqrt{r^2-x^2}\sqrt{\frac{r^2}{r^2-x^2}}dx \\
&= 2\pi \int_{-r}^r r dx = 2\pi \cdot 2r^2 = 4\pi r^2
\end{aligned}$$
關於圓周率的故事,到這裡先打住。還有很多故事,以後慢慢說,祝學習愉快。







老師好!
????
你的名字也太長了,不如取個筆名吧。
以後就叫你阿朗好了~