平時我們很少注意到,數學課本中提到的那些人名、定理、公式的發展順序。
因此,接下來的數學文章,我都會附上以下這個歷史年代表,讓讀者方便參照。
| 科學家、數學家 | 時間 | 特別事蹟 |
|---|---|---|
| Thales(泰利斯) | 約西元前640~548年 | 用相似形原理測出金字塔高度 |
| Pathagoras(畢達哥拉斯) | 約西元前580~496年 | 畢氏學派掌門人。該時期引發第一次數學危機。 |
| Zeno(季諾) | 約西元前460年 | 提出了四個關於運動不可能的悖論而知名 |
| Euclid(歐幾里德) | 約西元前325~265年 | 經典著作:幾何原本 |
| Archimedes(阿基米德) | 西元前287~212年 | 發現浮力定律 |
| Nicolaus Copernicus(哥白尼) 波蘭 | 1473-1543 | 提出日心說 |
| John Napier(約翰·納皮爾) | 1550~1617 | 完成對數表,簡化計算 |
| Galileo(伽利略) | 1564~1642年 | 現代觀測天文學之父 |
| Kepler(克卜勒) 德國人 | 1571~1630年 | 三大行星運動定律 |
| Descartes(笛卡兒) | 1596~1650年 | 解析幾何發明者 |
| Fermat(費馬) | 1601~1665年 | 律師,業餘數學家代表人物。 |
| Pascal(巴斯卡) | 1623~1662年 | 巴斯卡定理、巴斯卡三角形 |
| Newton(牛頓) | 1642~1727年 | 被蘋果砸到,發現了萬有引力 |
| Leibniz(萊布尼茲) | 1646~1716年 | 幾乎與牛頓同時發明了微積分 |
| James Bernoulli | 1654~1705年 | 優秀的柏努利家族成員 |
| John Bernoulli | 1667~1748年 | 優秀的柏努利家族成員 |
| Euler(歐拉) | 1707~1783年 | 超多產的數學家 |
| Gauss(高斯) | 1777~1855年 | 數學王子,19世紀最強數學家,沒有之一。 |
| Cauchy(柯西) | 1789~1857年 | 高中數學提到的柯西不等式,就是以此數學家命名。 |
| Weierstrass | 1815~1897年 | 構造出處處連續但處處不可微分的函數 |
| Riemann(黎曼) | 1826~1866年 | 著名的「黎曼猜想」至今無人能解。 |
| Dedekind(戴德金) | 1831~1916年 | 戴德金分割(Dedekind cut) |
| Cantor(康托爾) | 1845~1918年 | Cantor set 的引入者 |
| Poincar'e(龐加萊) | 1854~1912年 | 提出著名的龐加萊猜想 |
| Hilbert(希爾伯特) | 1862~1943年 | 提出23個最重要的問題(希爾伯特問題) |
| Einstein(愛因斯坦) | 1879~1955年 | 廣義相對論發明者 |
最近,高一數學進行到了對數。108課綱主要聚焦在常用對數(底數為10的對數),
所以對數律的運算也會少講一些,最明顯的就是省略「換底公式」的介紹。
這個單元的內容相較以往弱化。
如果同學有興趣了解一般底數的對數運算,
可以自行參考99課綱的教材。
這一篇文章,將從歷史的脈絡探討「對數」這個主題。
首先,你可以參照歷史年代表,對數的發明大約在十六、十七世紀。
這個時間點,世界還發生了哪些事情?
- 葡萄牙人麥哲倫(1480-1521)於1519年至1521年率領船隊環航地球。
- 麥卡托(1512~1594)在1569年利用等角變換的「麥卡托投影法」,
亦即利用正軸等角圓柱投影的方法繪製出新的世界地圖。 - 波蘭天文學家哥白尼(1473-1543)出版了《天體運行論》,
提出所謂的日心說。哥白尼提出了太陽中心論,
顛覆了當時普遍接受的地心說,開啟了天文學的革命。 - 德國天文學家克卜勒(1571-1630)於1609-1618年先後發表了
行星三大運動定律。克卜勒通過數學計算,
確定了行星繞太陽運行的橢圓軌道,進一步推動了天文學的發展。 - 伽利略(1564-1642)利用望遠鏡觀測天體,支持哥白尼的日心說,
並提出了許多重要的天文學發現,如木星的衛星和月球的山脈。
於1632年出版《關於托勒密和哥白尼兩大世界體系的對話》,
1638年出版《兩種新科學的對話錄》 - 威廉·哈維的血液循環理論(1628年):哈維發現了血液循環的機制,
為現代生理學奠定了基礎。 - 文藝復興在16世紀末期逐漸進入尾聲,但其思想和藝術影響依然深遠,
尤其是在意大利和歐洲其他地區。 - 荷蘭東印度公司(1602年成立)和英國東印度公司(1600年成立)
在亞洲展開商業活動,促進了全球貿易的擴展。 - 伊麗莎白一世女王(1533-1603年): 她的統治時期(1558-1603年)
被稱為英國的“黃金時代”,期間英國經濟繁榮,文化蓬勃發展,
如莎士比亞的戲劇創作。 - 十六、十七世紀,火藥技術和火器武器在歐洲戰爭中變得更加普遍。
這極大改變了軍事策略,並促進了城堡和防禦工事的設計演進。
納皮爾生活的十六、十七世紀,正是全球探索、科學研究和經濟發展的時代。
這一時期人們面臨的計算需求極其龐大且複雜,
特別是在天文學、航海、商業和軍事領域。
所以當對數發明之後,立刻迎來各地的讚譽。
利用對數來簡化乘除與開方計算的巨大優點,
甚至讓十八世紀著名的法國數學家拉普拉斯(1749~1827)
評價對數的發明「以及節省勞力而使天文學家的壽命延長了一倍。」
當時納皮爾對於對數的定義與現代不完全相同,
現在我們使用的定義是由歐拉(Leonhard Euler,1707-1783)
於1728年給出的,但是原創歸功於納皮爾。
納皮爾是怎麼定義對數運算呢?
他是從等差與等比數列的對照中定義了對數運算,
再花了近二十年歲月艱辛地完成對數表。
他是如何做的呢?
例如:在三角學中的和差化積、積化和差關係的觀察:
$$2sinAcosB=cos(A-B)-cos(A+B)\tag{1}$$
這個公式雖然在現行課綱已經被刪除了,
但是原理其實就是和差角公式加上符號代換而已,
同學不妨試著推導看看。
從上式(1)的觀察,我們發現在三角學中,
可以經由計算「和與差」來得到兩數的「乘積」。
這揭示了對數的關鍵思想:「將乘法轉化為加法」
另外,早在納皮爾之前,
就有數學家觀察到「等差數列」與「等比數列」的對應關係。
將等差數列中的加法操作轉化為等比數列中的乘法操作,可以簡化計算。
也就是說,如果需要計算兩個數的乘積,
可以通過對應的等差數列中的相加操作來達成。
例如,考慮一個等比數列 \(10, 100, 1000, 10000, …\) 以及一個對應的等差數列 \(1,2,3,4,…\)
那麼對應的關係可以總結為:等差數列的加法操作與等比數列的乘法操作相對應。
計算 $$10\times 100 = 1000$$ \(10\) 對應到等差數列的第 \(1\) 項,\(100\) 對應到等差數列的第 \(2\) 項。
這意味著乘積 \(10\times 100 = 1000\) 對應到等差數列的第 \(3\) 項。
因此,乘法可以通過等差數列中的加法來實現,這就是對數的核心思想。
根據這一發現,納皮爾編制了對數表。
該表將一系列數(等比數列)與對應的對數(等差數列)相連結。
當人們需要計算乘法時,他們可以查對數表,通過加法操作來簡化計算,
再通過查表找到結果。
舉個簡單的例子:
如果我們想計算 \(10^a\times 10^b\),其對應的加法是 \(a+b\)
查表後得到的對數值,經過反查即可得到乘積結果。
事實上,早在納皮爾之前就有數學家觀察到等差數列與等比數列之間的對應關係。
例如:法國數學家許凱(Nicolas Chuquet, 1445-1488)、
德國數學家史蒂費爾(Michael Stifel, 1487-1567)
納皮爾多做了什麼?
許凱與史蒂費爾等數學家只 考慮整數指數,
納皮爾將這個觀念推廣到指數為「連續的數」。
何謂連續的數?
當時納皮爾是從運動學的觀點切入:
兩質點在數線上的運動。
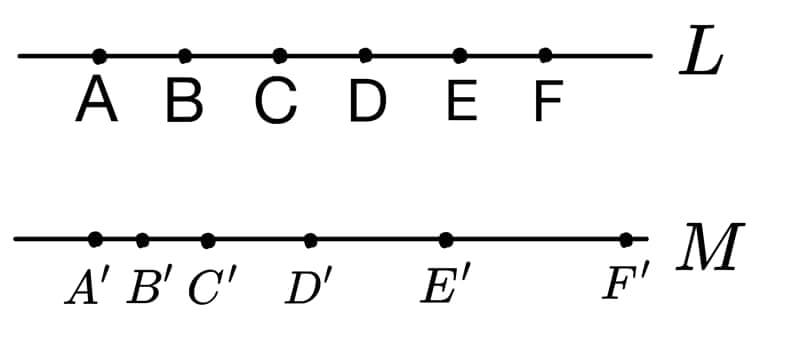
直線 \(L\) 上相鄰兩點的距離相同,而直線 \(M\) 上相鄰兩點間的距離成等比。
質點 \(P\)、\(Q\) 分別在直線 \(L\)、\(M\) 上,自 \(A\)、\(A’\)以相同初速出發。
經過相同時間,質點 \(P\) 通過 \(A\)、\(B\)、\(C\)、\(D\)、…,
質點 \(Q\) 通過 \(A’\)、\(B’\)、\(C’\)、\(D’\)、…,
其中 \(\overline{AB}=a\)、 \(\overline{AC}=2a\)、 \(\overline{AD}=3a\)、…
且 \(\overline{A’B’}=r\)、 \(\overline{A’C’}=r^2\)、 \(\overline{A’D’}=r^3\)、…
因此有了 \(na \leftrightarrow r^n\) 的對應關係,其中 \(n\) 是連續變動的數(很含糊的說法)。
那麼當 \(Q\) 走到任意點 \(x\),\(P\)會走到 \(y\) 點,
此時納皮爾將 \(y\) 視為 \(x\)的對數。
以我們在課堂上熟悉的寫法就是,$$r^n=m \ \ \longleftrightarrow \ \ n=log_{r} m$$ 亦即 \(n\) 是 \(m\) 的對數。
再回到前面提到的,納皮爾希望 \(n\) 為連續變動的數,
用現代的說法應該是,\(n\) 為任意實數。
然而,那個年代,對於分數指數的定義還不完善。
納皮爾為了讓計算時乘方增加得慢一點,使用較小的數 \(1-10^{-7}\) 當作底:
\(a_0 = 10^7\)、\(a_1=10^7(1-10^{-7})\)、\(a_2=10^7(1-10^{-7})^2\)、\(a_3=10^7(1-10^{-7})^3\)、…、\(a_{100}=a^7(1-10^{-7})^{100}\)
納皮爾將每個乘方的指數稱為「對數」。
用現代的術語來說,如果 \(N=10^7(1-10^{-7})^{L}\),
\(L\) 稱為 \(N\) 的「納皮爾對數」,記作 \(L=LogN\)。
也就是 $$Log N =log_{1-10^{-7}}\frac{N}{10^7}$$
當然,這樣的定義與我們現代的定義不盡相同。
後來,由倫敦萊斯罕的幾何學教授布里格斯(Henry Briggs, 1564-1631)提議,
將 \(1\) 的對數值定為 \(0\),並且將底改為 \(10\),並且重新製作對數表。
這個工作由布里格斯接手完成。
這篇文章就先寫到這邊,希望有助於同學學習對數時,
對於歷史的發展也能有一些了解。
祝學習順利,愉快。