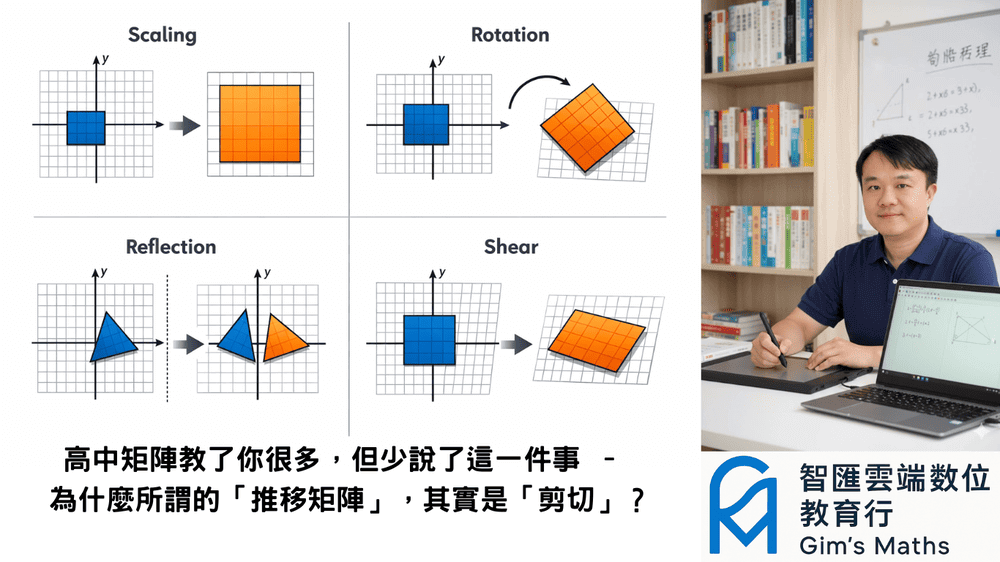
高中數學第四冊，關於平面上的線性變換，
我們學到了旋轉、鏡射、伸縮、推移。

為什麼我們要了解這四種矩陣？

原因是，平面上任何一個可逆的二階方陣，加上一個平移向量，
都可以寫成「伸縮、旋轉、鏡射、推移」的合成(高中課本)。

這是二階方陣的一種結構。

要留意的是，高中教科書的推移，更精確的說是「剪切」變換(「shear」transformation)。
推移這個名詞，一般而言是指「平移」。文章最後會再作說明。

為了讓定理更嚴謹，我們將敘述改寫如下：

「平面上任何一個可逆的二階方陣所代表的線性變換，
都可以寫成伸縮、旋轉、鏡射、剪切的合成。」

很多學生第一次學矩陣時，很容易將其視為一堆數字的運算。

事實上，矩陣是一種變換方式

透過它，可以改變圖形。

這一篇文章，我想帶你從「看見圖形的變化」開始，重新理解這個重要結論。

---

一、先把問題說清楚：矩陣在做什麼？

在平面上，我們常見的變換可以寫成

\[
f(\mathbf{x}) = A\mathbf{x} + \mathbf{b}
\]

這裡有兩個角色：

• \( A \)：二階可逆矩陣，負責改變形狀
• \( \mathbf{b} \)：一個固定向量，負責整個圖形的平移

先說一個很重要的觀念。

矩陣本身做不到平移。
所以「平移」一定來自 \( +\mathbf{b} \)。

因此，真正的核心問題只剩下一個：

任意一個可逆二階矩陣 \( A \)，
能不能只用「伸縮、旋轉、鏡射、剪切」來描述？

---

二、直觀錨點：請你盯著「單位圓」

在談任何證明前，我想請你先記住一個畫面。

想像平面上的單位圓

\[
x^2 + y^2 = 1
\]

把圓上每一個點 \( \mathbf{x} \)，都丟進 \( A\mathbf{x} \)。

你會看到一件事：

圓會變成橢圓。

這不是巧合，而是線性變換的本質。

換句話說，任何矩陣 \( A \) 做的事，本質上都是在回答：

這個圓，要怎麼被拉長、壓扁，
又要不要轉方向或翻面？

這個觀察，就是我們後面所有推導的心理錨點。

---

三、哪些變換「不改變長度」？

接下來，我們要先做一個非常關鍵的分類。

在平面變換中，有些操作會改變向量的長度，有些則不會。
而要看清楚矩陣 \( A \) 的結構，第一步，就是先找出「不改變長度」的那一類變換。

---

旋轉與鏡射的共同特徵

在所有常見的平面變換中，旋轉與鏡射看起來動作不同：
一個是在轉方向，一個是在翻面。

但它們其實有一個非常重要、而且可以直接檢驗的共同點。

對任意向量 \( \mathbf{x} \)，
經過旋轉或鏡射之後，向量的長度保持不變。

也就是說，這兩種變換只改變方向，
卻不會讓向量變長或變短。

---

為什麼要先抓住這一點？

既然旋轉與鏡射都不會改變長度，
那麼矩陣 \( A \) 裡面「真正負責改變長度」的部分，
就不可能來自這兩種變換。

因此，如果我們想把「伸縮」從 \( A \) 的作用中抽離出來，
就應該去找一個只和「長度如何改變」有關的矩陣。

換句話說，我們接下來要做的，是找出一個矩陣，
它專門記錄這件事：

向量經過 \( A \) 之後，
長度到底被放大了多少，或縮小了多少？

---

四、那麼，哪一個矩陣只和「長度變化」有關？

現在，我們已經知道一件事。

旋轉與鏡射不會改變向量的長度，
所以它們不可能是矩陣 \( A \) 中「伸縮」的來源。

接下來要問的問題是：
有沒有一個矩陣，可以把「長度怎麼改變」這件事單獨記錄下來？

為了回答這個問題，我們先看一個向量經過 \( A \) 之後，長度會如何變化。

---

向量長度在矩陣作用下的變化

取一個任意向量 \( \mathbf{x} \)，
經過矩陣 \( A \) 之後，變成 \( A\mathbf{x} \)。

新的長度平方可以寫成

\[\|A\mathbf{x}\|^2 = (A\mathbf{x})^T (A\mathbf{x})
\]

把括號整理後，可以得到

\[
\|A\mathbf{x}\|^2 =
\mathbf{x}^T A^T A \, \mathbf{x}
\]

這個結果非常關鍵。

它告訴我們：
向量長度的變化，並不是直接由 \( A \) 本身決定，
而是完全被 \( A^T A \) 這個矩陣控制。

---

為什麼是 \( A^T A \)？

這裡要特別注意一件事。

不論原本的矩陣 \( A \) 裡面包含多少旋轉或鏡射，
在 \( A^T A \) 中，這些「只改變方向、不改變長度」的效果，
都會被抵消掉。

留下來的，只剩下和長度變化有關的資訊。

也就是說，\( A^T A \) 扮演的角色非常單純：

它只負責記錄
向量在各個方向上，究竟被放大或縮小了多少。

---

接下來會發生什麼？

一旦我們找到這個「只描述伸縮」的矩陣，
就可以把它從 \( A \) 中抽離出來，
剩下的部分，自然只可能是旋轉或鏡射。

接下來，我們就要進一步利用 \( A^T A \) 的性質，
把矩陣 \( A \) 的幾何結構完整拆解出來。

---

五、對稱矩陣在幾何上的意義（高中延伸）

前一段我們看到，向量長度如何改變，完全由 \( A^T A \) 決定。
接下來，事情會變得清楚，是因為 \( A^T A \) 還有一個非常關鍵的性質。

\[
(A^T A)^T = A^T A
\]

也就是說，\( A^T A \) 是一個對稱矩陣。

這個性質，讓它的幾何意義變得非常單純。

---

對稱矩陣代表的幾何結構

任何一個二階實對稱矩陣，都可以找到兩條互相垂直的方向，
使得矩陣在這兩個方向上的作用只剩下伸縮。

換句話說，存在一組互相垂直的座標軸，使得在這組座標下，
矩陣不再造成旋轉或剪切，而只是在不同方向上做伸縮；
若某一方向的伸縮倍率為負，則同時包含鏡射。

用數學語言表達，就是存在一個正交矩陣 \( Q \)，使

\[
A^T A = Q
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
Q^T
\]

這裡可以這樣理解：

• \( Q \) 的作用，只是把座標軸轉到「正確的方向」
• \( \lambda_1, \lambda_2 \) 是正數，描述在這兩個方向上的伸縮強度

---

六、把「純伸縮」單獨抽離出來

既然 \( A^T A \) 描述的是伸縮效果的「平方」，
那麼下一步就非常自然了。

我們希望找到一個矩陣，它本身就只負責伸縮，而平方之後剛好等於 \( A^T A \)。

因此定義

\[
S = Q
\begin{pmatrix}
\sqrt{\lambda_1} & 0 \\
0 & \sqrt{\lambda_2}
\end{pmatrix}
Q^T
\]

直接計算可以得到

\[
S^2 = A^T A
\]

這個矩陣 \( S \) 的幾何意義非常清楚。

它表示：
沿著兩條互相垂直的方向，
分別做 \( \sqrt{\lambda_1} \) 與 \( \sqrt{\lambda_2} \) 倍的伸縮。

到這一步為止，
矩陣 \( A \) 中所有與「長度改變」有關的部分，已經被完整地抽離出來了。

---

七、剩下的部分，只可能是旋轉或鏡射

既然伸縮已經被 \( S \) 負責完畢，
那麼矩陣 \( A \) 剩下來的部分，還能做什麼？

我們直接定義

\[
R = A S^{-1}
\]

接著檢查它對長度的影響。

\[
R^T R =
(A S^{-1})^T (A S^{-1})
=S^{-1} A^T A S^{-1}
=S^{-1} S^2 S^{-1}=I
\]

這個結果意味著一件非常重要的事。

\[
R \text{ 不改變向量長度，也保持角度}
\]

在平面上，這樣的變換只有兩種可能：

• 旋轉
• 鏡射（或鏡射後再旋轉）

---

八、矩陣的結構終於完整呈現

現在，我們已經得到

\[
A = R S
\]

把它放回原本的仿射變換

\[
f(\mathbf{x}) = A\mathbf{x} + \mathbf{b}
\]

就可以寫成

\[
f(\mathbf{x}) = R S \mathbf{x} + \mathbf{b}
\]

用幾何語言來說，整個過程是：

先伸縮
再旋轉或鏡射
最後整個平移

這正是平面上仿射變換的完整結構。

---

九、這個結論在數學中的位置

這樣的分解，在數學中被稱為「極分解」。

它不是為了考試而設計的技巧，而是來自一個非常根本的問題：

如何把「形狀的改變」與「方向的改變」分開來看？

這個想法後來在物理、電腦圖學、工程分析中反覆出現。

而在高中階段，你已經可以用線性代數的語言，看見這個結構的雛形。

---

十、給正在學矩陣的你

如果你曾經覺得矩陣只是一堆計算步驟，
不妨先停下來，用另一個角度欣賞。

矩陣不是數字的堆疊。
它是一套用來描述幾何變形的語言。

當你能把一個矩陣理解成：

怎麼拉
怎麼轉
要不要翻
以及最後要不要整個搬走

你就真的開始理解線性代數了。

---

補充說明：教材中的「推移矩陣」，其實是剪切矩陣

在高中教材中，常會看到下列矩陣被稱為「推移矩陣」：

\[
\begin{pmatrix}
1 & k \\
0 & 1
\end{pmatrix},
\quad
\begin{pmatrix}
1 & 0 \\
k & 1
\end{pmatrix}
\]

這裡需要補上一個較為嚴謹的數學說明。

---

從線性代數的角度來看，這不是平移

真正的平移變換是

\[
(x,y) \longmapsto (x+p,\;y+q)
\]

它一定會讓原點移動：

\[
(0,0) \longmapsto (p,q) \neq (0,0)
\]

但對於教材中的這類矩陣變換，例如

\[
(x,y) \longmapsto (x+ky,\;y)
\]

代入原點可得

\[
(0,0) \longmapsto (0,0)
\]

原點保持不動。

因此，從線性代數的嚴格定義來看，這類變換不屬於平移。

---

正確的數學名稱：剪切

上述這類變換，在數學上有一致且明確的名稱，稱為剪切變換。

其對應的矩陣稱為剪切矩陣。

這類變換具有以下特徵：

• 原點固定
• 面積不變（行列式為 1）
• 形狀改變
• 一個座標保持不變，另一個座標依線性比例改變

---

為什麼高中教材仍使用「推移」這個詞？

教材使用「推移」這個詞，並不是在進行線性代數的嚴格分類，
而是採取一種幾何直觀的描述方式。

從圖形上看，矩形的一條邊彷彿被往旁邊推開，
形成平行四邊形，因此以「推移」來形容其視覺效果。

需要特別理解的是，這裡的「推移」描述的是操作感受，
而不是線性代數中「平移」這個專有名詞。

---

這個釐清反而讓結構更清楚

一旦我們清楚區分：

• 剪切：可由二階方陣表示，原點固定
• 平移：無法由二階方陣表示，必須引入仿射變換

反而更容易理解：

不是所有「看起來在位移」的變形，都是平移。
有些只是內部被推歪，但原點其實沒動。

---

結語

這篇文章，並不是一篇嚴格的線性代數推導，
而是一段為高中生準備的延伸閱讀。

在課本中，矩陣常常以計算為主，
步驟清楚，但目的不一定明確。
這裡嘗試做的，是換一個角度看矩陣：
不急著算，而是先問——
它到底在對圖形做什麼？

當我們開始用「伸縮、旋轉、鏡射、剪切」來描述矩陣，
矩陣就不再只是數字排列，
而是一種描述幾何變形的語言。
即使有些說法不追求最嚴格的定義，
只要能幫助你在學習時建立畫面、抓住結構，
這樣的理解本身就是有價值的。

如果這篇文章能讓你在看到矩陣時，
多想一秒「它在怎麼拉、怎麼轉、怎麼推歪」，
那麼它的目的就已經達成了。

文中若有不夠周全、或仍可修正補充之處，
也歡迎讀者提出討論與指正。
數學的理解，本來就是在不斷修正中慢慢成形的。

文章就先寫到這裡，祝學習愉快。 Gim Chen 2026.2.1 於週日早晨的思考筆記

---