最近班上學生問了一道數學題，我想了一下，覺得挺有意思，但是課程緊湊無暇將思考過程寫下來，特撰此文分享。

題目敘述如下：

阿拉丁做了21個小點心，之後和阿拉甲、阿拉乙、阿拉丙跟神燈一起先後把它們全吃光。最後大家報告各自所吃的數量：
神燈：「我吃了剩下的個數的三分之二」
阿拉甲：「我吃了剩下的個數的一半」
阿拉乙：「我吃了剩下的全部」
阿拉丙：「每個人吃的個數皆不相同」
阿拉丁：「我吃了剩下個數的一半」
(1) 神燈是第幾個吃的？
(2) 承(1)題，神燈吃了幾個小點心？

整個問題有兩個變項，所以顯得有些複雜：

• 這五個人吃的順序
• 每個人吃的個數

首先，我們先來決定順序。阿拉乙吃了剩下的全部，因此他應該是最後一個吃。接著我們來決定第一個吃的是誰。

阿拉乙和阿拉丁吃了剩下個數的一半，全部有21個點心，不可能分成一半，因此判斷阿拉乙與阿拉丁不會是第一個吃。

如果神燈第一個吃呢？排序如下：神燈，___、___、___、阿拉乙。
神燈吃了\(21\times \frac{2}{3}=14\)個，剩下7個，不可能分一半，因此第二位必然是阿拉丙，而且他必然吃掉奇數多個，如此才會剩下偶數個讓阿拉甲與阿拉丁吃剩下的一半。

情況1：阿拉丙吃1個，則阿拉甲與阿拉丁無論順序如何，皆不可能吃掉剩下個數的一半。
情況2：阿拉丙吃3個，阿拉甲與阿拉丁無論順序如何，必然一位吃2個，一位吃1個。這樣會造成有兩個人吃1個。
情況3：阿拉丙吃5個，最後剩下兩個，不夠剩下3個人分。

因此我們可以先排除神燈第一個吃的情形，僅剩下一種可能，阿拉丙排第一位。
排序如下：阿拉丙，___、___、___、阿拉乙。

情況1：阿拉丙吃1個。第2位必然是阿拉甲或阿拉丁吃剩下的一半。不失一般性，假設第二位是阿拉甲吃10個，那麼第三位必然是阿拉丁吃5個。剩下5個不可能讓神燈吃剩下的三分之二。

阿拉丙吃2個剩19個不可能被分一半或三分之二，不需考慮。

情況2：阿拉丙吃3個，剩18個。如果第二位是阿拉甲(或丁)，再吃掉9個，剩9個。第三位必然是神燈吃掉6個，剩3個不可能被阿拉丁(或甲)吃掉一半。

阿拉丙吃4個，剩17個，不可能被分一半或三分之二，不需考慮。

情況3：阿拉丙吃5個，剩16個。第二位必然是阿拉甲(或丁)，再吃掉8個，剩8個。第三位必然是阿拉丁(或甲)吃掉4個，剩4個，不可能讓神燈吃掉三分之二。

情況4：阿拉丙吃6個，剩15個，第二位必然是神燈吃掉10個，剩5個，不可能被阿拉甲或阿拉丁吃掉剩下的一半。

情況5：阿拉丙吃7個，剩14個，第二位必是阿拉甲(或丁)，再吃掉7個，與條件不符。

阿拉丙吃8個，剩13個，不可能被吃一半或三分之二，不須考慮。

情況6：阿拉丙吃9個，剩12個。第二位可以是阿拉甲、阿拉丁或神燈。
如果第二位是阿拉甲吃6個，剩6個：
第三位是阿拉丁吃3個，第四位神燈吃2個，最後阿拉乙吃1個。我們找到一組可能了。
第三位是神燈吃4個，第四位阿拉丁吃1個，最後阿拉乙也吃1個，不符合條件。

如果第二位是神燈吃8個，則會剩4個：
第三位是阿拉甲吃2個，剩2個，則阿拉丁與阿拉乙各吃一個，與條件不符。由以上討論，此題的解是唯一的。排序如下：

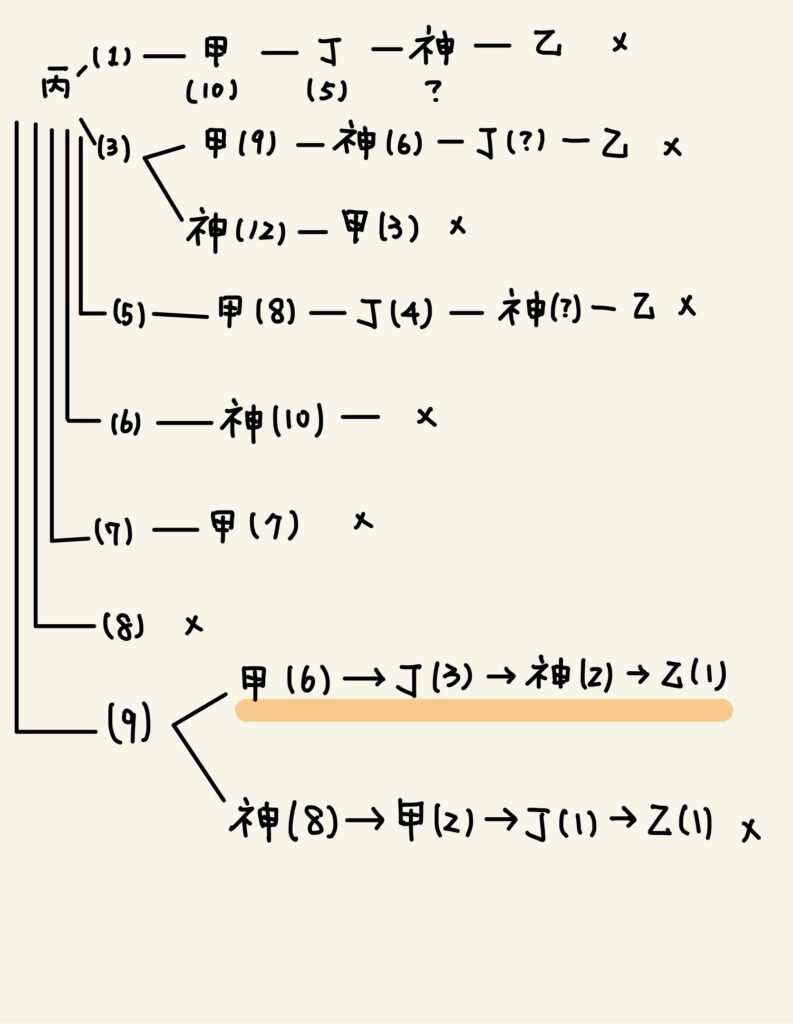
阿拉丙(吃9個)、阿拉甲(吃6個)、阿拉丁(品3個)、神燈(吃2個)、阿拉乙(吃1個)。

總結

分析過程採用「阿拉丙」吃的個數進行分類，然後再逐一刪除不可能的情況，討論過程可以採用樹狀圖會較有條理：