前言

最近農曆新年，看到一篇文章，標題是，「為什麼現在春節年味愈來愈淡？」引起許多七、八年級生的共嗚。

作為七年級生，我也曾經歷過很有年味的年代。當時過年時，最常進行的娛樂之一，就是玩撲克牌，小賭怡情。

賭博這件事，可能是最古老的休閒活動之一，而骰子則是賭博常用的工具，在許多古文明中曾以各種不同的樣貌出現。

賭博和遊戲是機率論發展的一個重要動機。在16世紀歐洲，數學家如Cardano和Pascal就開始研究擲骰子和撲克牌遊戲，這導致了機率的早期發展。

17世紀的保險業也促使機率論的發展。人們開始研究風險、損失和賠償，並使用機率來評估這些風險，進而發展出保險和風險管理的數學方法。

18世紀和19世紀，統計學逐漸成為一門重要的學科。機率論成為統計學的基礎，用於描述和解釋不確定性，並提供統計推論的理論基礎。

物理學、化學、生物學等自然科學領域中的實驗和觀測也需要處理不確定性。機率論提供了一種描述和分析隨機現象的數學工具，例如粒子運動、分子碰撞、生物遺傳等。

20世紀，隨著金融和經濟學的發展，對風險、波動和市場行為的理解變得至關重要。機率論在金融和經濟學中得到廣泛應用，例如在選擇定價、風險管理和投資組合改善方面。

總的來說，機率論的發展源於人類對於不確定性和隨機現象的探索和理解的需求，並成為許多領域中解決問題的基本工具之一。

課程內容回顧

「機率」這個主題是高中數學第二冊的內容(南一版3-2、龍騰版單元06)。以下截取南一版課本的其中一段敘述讓同學回憶一下：

西方的學者在十七世紀開始發展機率理論，當時是為了處理如骰子、輪盤、撲克牌等遊戲，當時的法國人梅雷(Chevalier de Mere, 1607~1684) 還曾寫信給巴斯卡請教擲骰子與分配賭金的問題，這些問題帶動了對機率的研究。1654年，巴斯卡與數學家費瑪(Pierre de Fermat, 1601~1665，法國) 通信討論這些問題，二人往返的書信開啟了探討機率理論的大門。

接著課本就開始進入了古典機率的定義、例題及機率性質的探討。

這一篇文章，我們要再回來看這兩個問題。

歷史回顧

當時數學家梅雷寫信給巴斯卡問的兩個問題中，一個是骰子問題，另一個則是分配賭金的問題。

(1) 骰子問題 (Problem of Dice)：兩個骰子要擲多少次才能使出現兩個 $6$ 點的機率不小於 $50\%$

換句話說：「兩個骰子擲 $n$ 次，至少出現一次兩個 $6$ 點的機率不小於 $50\%$，則 $n$ 至少是多少？」

我們可以使用反面做法來處理，即計算「沒有一次出現兩個 $6$ 點的機率」，然後用 $1$ 減去這個機率。

已知，兩個骰子出現 $6$ 點的機率是 $\frac{1}{36}$，則未出現兩個 $6$ 點的機率是 $1-\frac{1}{36}=\frac{35}{36}$

擲 $n$ 次都沒有一次出現兩個 6 點的機率為 $(1-\frac{1}{36})^n$，要使這個機率不小於 $50\%$，即

$$1-(\frac{35}{36})^n \geq 50\%$$ 移項整理可得
$$(\frac{35}{36})^n \leq \frac{1}{2}$$ 不等式兩邊取對數可解得 $$n\geq 24.67$$ 也就是說，至少要擲 $25$ 次才行。這個問題以我們目前學到的高中數學知識可以輕鬆解決。接著我們來看第二個問題。

(2) 得分問題(Problem of points)：

「每人各出32個金幣為賭注，約定先贏3分者勝，若第一人已先得2分，第二人得1分的時候比賽中斷無法繼續，應如何分配賭注才公平？」

在巴斯卡與費馬之前，也曾有不同的數學家討論過得分問題：

義大利數學家 帕奇歐里(Luca Pacioli, 1445-1517) 在其著作《算術幾何及比例性質之摘要 1494》也曾提到類似的問題
兩個人在進行一場公平的賭博，賭局在一個人贏得6局之後分出勝負。賭博進行到一個人贏得5局、另一個人贏得3局時中斷，那麼賭金應該如何分配呢？

帕奇歐里認為賭注應該按照 $5:3$ 的方式分配，讀者可停下來想想，這是合理的嗎？

如果比賽時，一人贏得1局，另一人贏0局時中斷，那麼贏1局的人可贏得所有賭注？

可是此時贏0局的人會提出抗議，他之後也有贏的機會，只輸一局他的錢就全部沒了，這樣子分配實在難以接受。

當時梅雷寫信請教巴斯卡時，巴斯卡將這個問題告訴另一位法國知名數學家費馬，費馬的做法是列出所有情況，然後根據最後所有結果各佔的比例來分配賭金。我們以總分5分，先得3分者獲勝為例。

假設A已得1分，B尚末得分。以 $a$ 代表 A 得分， $b$ 代表 B 得分。我們以樹狀圖呈現如下：

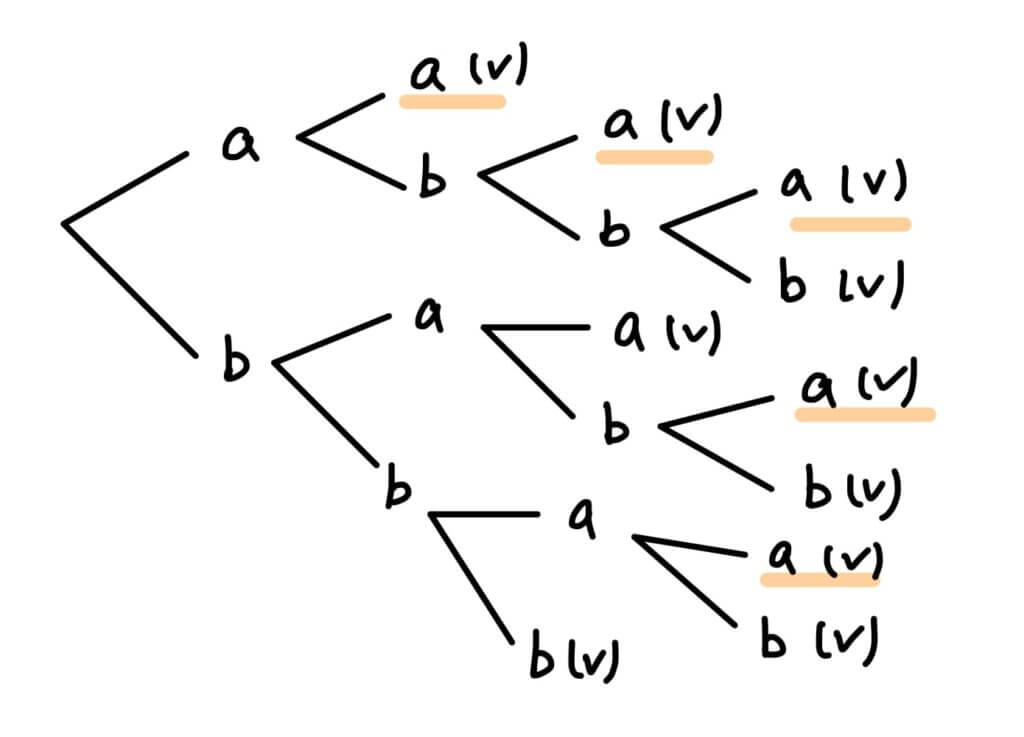
接著計算 A、B各獲勝的機率
$$\begin{aligned} P(A勝) &= (\frac{1}{2})^2+(\frac{1}{2})^3 +(\frac{1}{2})^4\times 4 = \frac{11}{16} \\ P(B勝) &= 1-\frac{11}{16} = \frac{5}{16} \end{aligned}$$

因此，最後賭金是採用 $11:5$ 的比例分配。可是這樣的做法有個缺點，就是不易推廣成一般的情形。巴斯卡為了研究這個問題的通解，進一步寫了《論算術三角》這一篇論文。我們先將問題重新敘述一次：

「假設第一人缺 $r$ 分後獲勝，第二人缺 $s$ 分後獲勝，其中 $r, s$ 不小於 $1$，如果整場比賽就此停住，那麼賭注應該如何分配呢？」

可以知道，接下來最多還須比 $r+s-1$ 局才能分出勝負。巴斯卡認為他們獲勝的機率可以用二項展開式的係數加以說明。

令 $n=r+s-1$，則考慮 $(a+b)^n$，以 $a$ 代表第一人獲得一局，$b$ 代表第二人獲得一局的情形。

$$(a+b)^n=C^n_0 a^n+C^n_1a^{n-1}b+C^n_2a^{n-2}b^2+…+C^n_{s-1}a^{n-s+1}b^{s-1}+…+C^n_n b^n$$

接下來來解讀這個式子所代表的意思，以總分5分，先得3分者獲勝且A已得1分，B尚未得分為例：
$$(a+b)^4 = C^4_0 a^4 +C^4_1 a^3b + C^4_2 a^2b^2+ C^4_3 ab^3 + C^4_4 b^4$$

第一項：A 贏4局，一種排列數為 $aaaa$，此種情況 A 獲勝
第二項：A 贏3局，B 贏1局，四種排列數為 $aaab$、$aaba$、$abaa$、$baaa$，這四種情況都是 A 獲勝
第三項：A 贏2局，B 贏2局，六種排列數為， $aabb$、 $abab$、 $abba$、 $baab$、 $baba$、 $bbaa$ 這六種情況皆為 A 獲勝
第四項：A 贏1局，B 贏3局，四種排列數為， $abbb$、 $babb$、 $bbab$、 $bbba$ 這四種情況皆為 B 獲勝
第五項：B 贏4局 ，一種排列數為 $bbbb$，此種情況 B 獲勝

由以上分類可看出，A 最後獲勝的情形有 $11$ 種，B 最後獲勝的情形有 $5$ 種。
我們可以觀察此例子，再推廣至一般的情形。以此例來說，
$$A \ 獲勝的情形有\ C^4_0 + C^4_1 + C^4_2 = 11 \ 種$$
再回來看一般的情形，
$$第一人獲勝的情形有\ C^n_0 + C^n_1 + C^n_2 + … + C^n_{s-1} \ 種$$

也就是說，在第二人贏得 $s$ 分之前，第一人先贏得了 $r$ 分，此時第一人獲勝。

因此 A 分配所得的賭注與全部賭注的比應為 $$\sum_{k=0}^{s-1}C^n_k:2^n$$

至此就可以一般化分配賭金的問題，至於如何使用嚴格的數學歸納法證明，這裡就不再贅述。

歡迎訂閱 高中數學數位學習電子報

筆者簡介

機率在生活中扮演關鍵角色，它不僅指引我們做決策的方向，還幫助我們評估風險和預測結果。透過機率思維，我們能更明智地規劃未來、做出理性選擇，提高生活品質。機率觀念應用於各領域，從金融到醫療，都能協助我們更有效地應對不確定性，為個人和社會創造更穩定且可靠的發展基礎。