提到迪卡兒,大多數人的第一反應可能是那句響徹哲學史的名言:「我思,故我在」(Cogito, ergo sum)。
這句話奠定了近代哲學的基礎,讓他被譽為「近代哲學之父」。
然而,許多人可能不知道,這位哲學巨擘在數學領域的貢獻,
同樣具有劃時代的意義——甚至可以說,如果沒有他,
我們今天的科技文明可能要晚好幾個世紀才會出現。
看看你手機裡的 Google Maps,看看建築師電腦裡的 CAD 設計圖,再看看股市分析的折線圖。
這些我們習以為常的工具,背後都有一個共同的基礎:直角座標系統(Cartesian Coordinate System)。
沒錯,這個我們從國中數學課就開始畫的 \(X\) 軸與 \(Y\) 軸,正是源自於迪卡兒的創見。
一場關於「蒼蠅」的幾何革命
在迪卡兒之前,數學的世界是分裂的。
當時的數學家主要分為兩派:一派鑽研「代數」,處理抽象的符號與方程式運算;
另一派則傳承自古希臘的歐幾里得,專注於「幾何」,研究圖形的形狀、角度與面積。
這兩者就像是兩條平行線,雖然都是數學,卻老死不相往來。
代數家覺得幾何太依賴直覺,不夠嚴謹;
幾何學家則認為代數只是一堆枯燥的符號,缺乏直觀的美感。
直到 1637 年,迪卡兒出版了著名的《幾何學》(La Géométrie)。
在這本書中,他做了一件前無古人的事:他把代數與幾何徹底結合了起來。
關於這場革命的靈感來源,有一個廣為流傳(雖然可能是後人杜撰,但極具啟發性)的故事:
傳說中,體弱多病的迪卡兒習慣在床上思考。
某個早晨,他躺在床上盯著天花板看,發現一隻蒼蠅在天花板上爬行。
他突然想到一個問題:「我要如何精確地向別人描述這隻蒼蠅的位置?」他意識到,只要以天花板的兩個相鄰邊牆角作為基準線,
測量蒼蠅距離這兩面牆的垂直距離,就能得到兩個數字。
無論蒼蠅爬到哪裡,只要這兩個數字確定了,蒼蠅的位置也就確定了。
這個看似簡單的「定位」想法,就是解析幾何的雛形。
迪卡兒的偉大之處,在於他將幾何圖形「翻譯」成了代數語言。
直線不再只是一條畫在紙上的痕跡,它變成了 $$ax + by = c$$
圓不再只是一個完美的圈,它變成了 $$x^2 + y^2 = r^2$$
「適當的座標化,可有效簡化問題。」 這句話不僅是數學技巧,更是一種思維的升級。
迪卡兒讓我們明白,複雜的幾何難題,可以透過座標系的轉換,變成標準化的代數運算來解決。
他架起了一座橋樑,讓人類可以用「計算」來駕馭「圖形」,
這直接促成了後來牛頓與萊布尼茲微積分的誕生。
臥床思考的特權:把「弱點」變成「優勢」
迪卡兒能有如此深刻的洞見,與他獨特的成長背景密不可分。
他於 1596 年出生在法國一個富裕的律師與醫生世家。
然而,上天給了他優渥的家境,卻沒給他健康的身體。
他自小體弱多病,臉色蒼白,還有乾咳的毛病,醫生甚至曾預言他活不過成年。
因為身體太差,當他 12 歲進入當時歐洲最頂尖的耶穌會學校——拉弗萊什學院(Collège Royal Henry-Le-Grand)
就讀時,校長夏萊神父給了他一項特殊的「特權」:他可以不必像其他學生那樣早起晨禱和上早自習,
允許他睡到自然醒,甚至整天待在床上。
這對當時嚴格的寄宿學校來說簡直是不可思議的例外。
但正是這段「賴床」的時光,成就了迪卡兒。
不像其他孩子在睡眼惺忪中背誦課文,迪卡兒在那些長長的、安靜的早晨裡,
擁有了最奢侈的東西:獨處與思考的時間。
他後來回憶道:「在那些長長的安靜的早晨所進行的沉思,乃是產生我的哲學和數學思想的真正源泉。」
這給了我們現代人一個極大的反思:我們是否太過忙碌了?
在現代社會,忙碌被視為一種美德。
學生從早自習忙到晚自習,下課後還有補習班;
上班族在會議與郵件中疲於奔命。
我們不斷地接收資訊,卻很少留出時間來「反芻」這些資訊。
迪卡兒的故事告訴我們,真正的智慧往往不是在忙碌的書寫中誕生,
而是在安靜的沉思中浮現。
有時候,稍微「慢下來」,甚至「無所事事」一下,
反而是大腦進行深度連結的最佳時刻。
我懷疑,所以我學習:拒絕盲從的勇氣
在拉弗萊什學院,迪卡兒接觸到了當時最先進的學術內容,包括拉丁文、邏輯學、物理學和神學。
然而,這位資優生在畢業時,卻說了一句耐人尋味的話:
「我從老師那裡學到的東西,不如我從懷疑與思考中學到的多。」
這並不是說他狂妄自大,而是他敏銳地發現了當時教育體系的漏洞。
他發現教科書裡的許多理論,往往建立在模糊不清的假設上,
或者是引經據典自古人的權威,缺乏嚴謹的邏輯推導。
他說:「除了數學之外,沒有什麼是確定的。」
這種「懷疑精神」成為了他後來治學的核心方法,
也就是著名的「方法論」(Discourse on the Method)。
他主張,在接受任何真理之前,必須先經過嚴格的懷疑。
他不等待老師告訴他答案,也不依賴書本上的標準解法,
而是試圖從零開始,用自己的理性去推導出整個世界。
反觀現在的教育現場,我們是否失去了這種「懷疑」的能力?
現今補習風氣盛行,許多學生從小就被訓練成「解題機器」。
為了考高分,我們習慣了「填鴨式」的餵養:
- 老師說:「這個公式背起來,考試會考。」學生就背起來。
- 補習班教:「看到這個題目,就套這個解法。」學生就照做。
這種學習方式雖然在短期內能換來分數,但長期來看,
卻扼殺了「舉一反三」的能力。
當學生只知道「怎麼做(How)」,卻不知道「為什麼(Why)」的時候,
一旦題目稍微變形,或是遇到課本以外的未知問題,
他們就會立刻卡住,陷入恐慌。
這就是考試導向教學最大的盲點:只重視效率,卻忽略了理解;
只在乎標準答案,卻犧牲了探索過程。
自主學習:從迪卡兒到現代數學家
如果你細讀迪卡兒的學習歷程,你會發現,他從來不是靠老師「手把手」教會的。
他的數學成就,很大程度上來自於他離開學校後,在遊歷歐洲、參軍、隱居的過程中,
不斷自我對話、自我挑戰的結果。
「自主學習」不是一門掛在課表上的課程,而是一種生活態度,
更是一項需要終生實踐的能力。
這不僅僅是迪卡兒的故事。在我們這個「數學家系列」接下來即將介紹的人物中,
你會發現一個驚人的共通點——無論是「數學王子」高斯(Gauss)、「多產天才」歐拉(Euler),
還是物理與數學的巨人牛頓(Newton),他們幾乎沒有一個人是完全依賴學校教育而成功的。
- 歐拉在視力幾乎喪失的情況下,依然憑藉著強大的心算與記憶力,
推導出無數公式,因為他對數學的熱情超越了身體的障礙。 - 牛頓在 1665 年倫敦大瘟疫期間,學校停課,他被迫回到鄉下老家。
正是在那段沒有老師、沒有同學的「隔離」時光裡,他獨自發明了微積分、發現了萬有引力。 - 高斯小學時就能快速算出 1 到 100 的總和,不是因為老師教過公式,
而是他觀察到了數列的對稱性。
這些偉大的靈魂,都有一個共同特質:不等待制度的安排,不依賴他人的引導,
而是主動尋找問題、勇敢提出假設、獨立進行探索。
結語:成為一個有思考力的學習者
在這個資訊爆炸的 AI 時代,獲取知識已經不再是難題。
你隨時可以在網路上找到微積分的教學影片,
或是查詢解析幾何的公式證明。
我們缺少的不是知識,而是像迪卡兒那樣的「思考力」。
學習數學,不該只是為了應付考試,或是算出一個正確的數字。
數學的本質,是一種邏輯訓練,是一種看世界的方式。
就像迪卡兒透過座標系,看見了幾何圖形背後的代數秩序;
我們也應該透過學習,練習看穿複雜問題背後的本質。
如果你正對學習感到迷惘,覺得每天被考卷追著跑卻不知道意義何在;
或者你已經離開學校多年,覺得大腦逐漸僵化。希望迪卡兒的故事能給你一些啟發:
- 給自己一點「留白」的時間:不要把生活填得太滿,思維需要空間才能奔跑。
- 培養「懷疑」的習慣:不要輕易接受現成的答案,
試著問「為什麼是這樣?」、「有沒有別的方法?」。 - 練習「自主學習」:不要等著別人教你,試著自己去定義問題,並尋找解決方案。
願這一系列的數學家故事,不只是帶你認識歷史上的偉人,
更能夠填補課本有限篇幅裡的空白,點燃你心中那盞理性的燈火。
讓我們像迪卡兒一樣,在座標的交會點上,找到屬於自己的思考定位。
解題指引:選擇適當座標,可有效簡化計算
問題:在三角形\(ABC\)中,\(\overline{AB}=\overline{AC}\),\(D\)是\(\overline{BC}\)的中點,
\(E\)是由\(D\)向直線\(AC\)作垂線的垂足而\(F\)是\(\overline{DE}\)的中點,
證明:直線\(\overline{AF}\) 垂直\(\overline{BE}\)
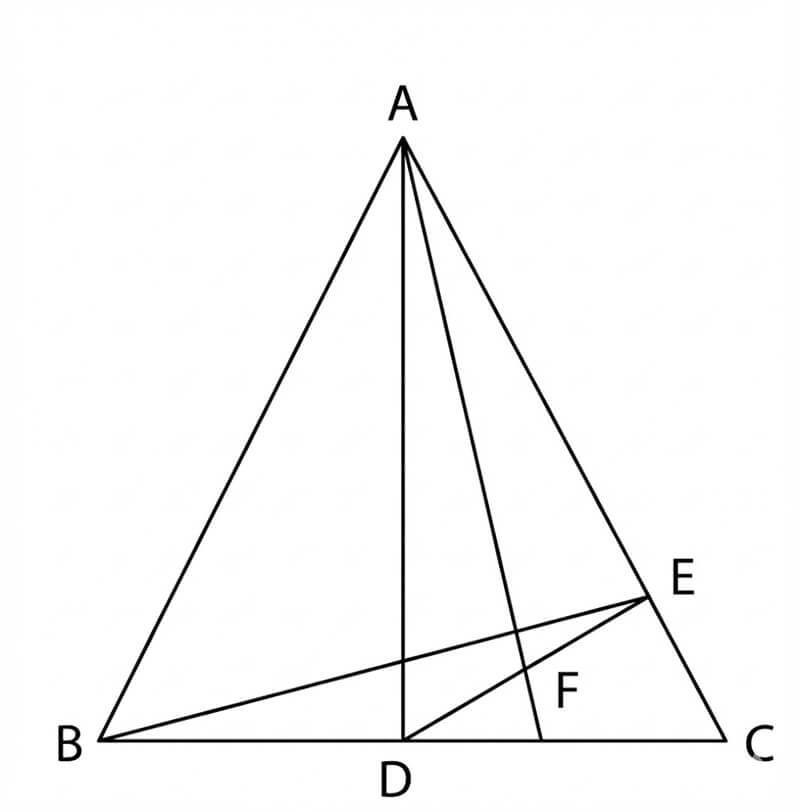
這一題用純幾何處理不是件容易的事,
所以座標化是不錯的選擇,
但是如果沒有選到適當的座標,過程也不會太順利。
例如,你可以試試將 \(D\) 點設為原點,而且 \(A(0,a)\)、\(B(-b,0)、C(b,0)\),
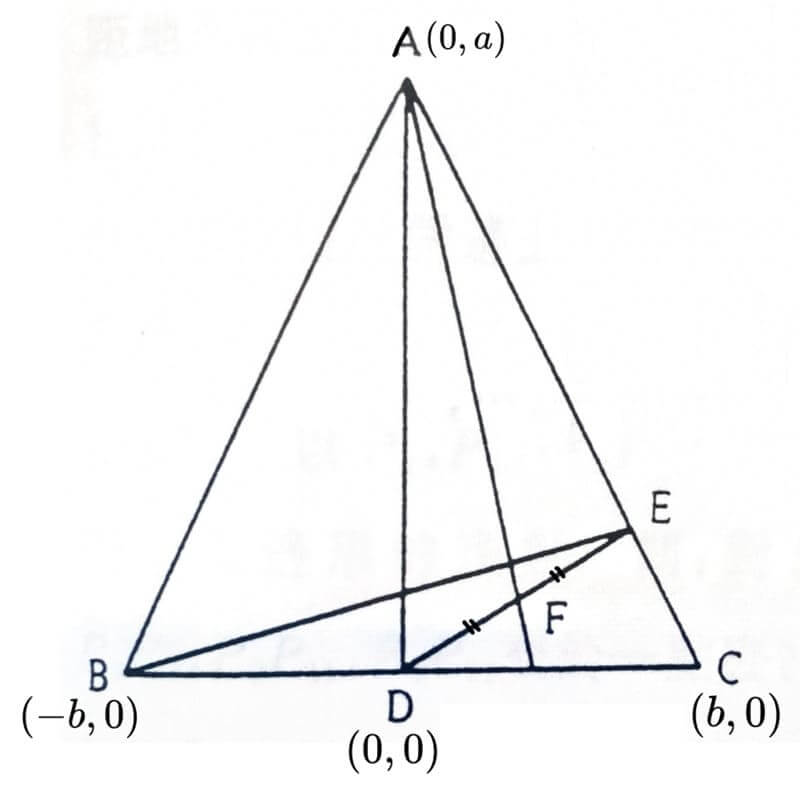
直線 \(AC\) 的方程式為 $$ax+by=ab \tag{1}$$
因為直線 \(DE\) 與直線 \(AC\) 垂直,且通過點 \((0,0)\),則直線 \(DE\) 為$$bx-ay=0 \tag{2}$$
由(2)知 \(y=\frac{b}{a}x\) 代入(1) $$ax+b\cdot\frac{b}{a}x=ab$$ 移項整理可得
因此點 \(F\) 的坐標為
接下來計算直線 \(AF\) 與 \(BE\) 的斜率
因此
現在換另一種坐標化,如圖所示:
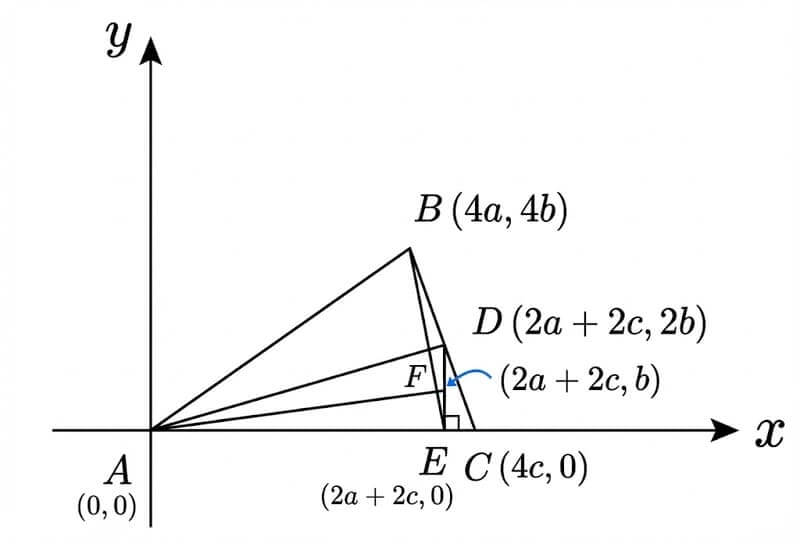
接著計算似乎簡單了不少:因為
因此,