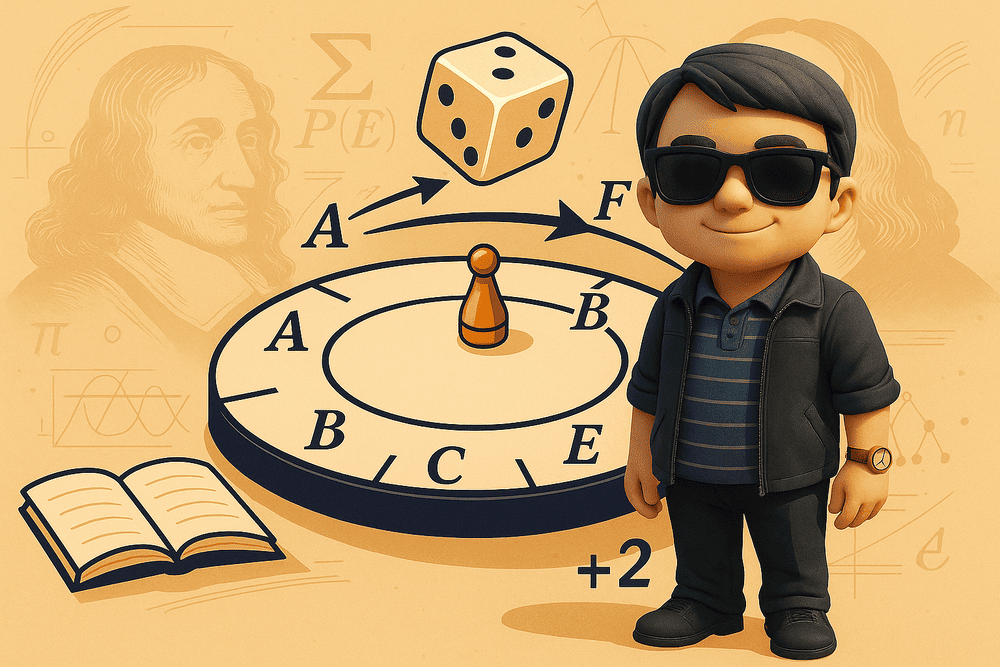高中數學第二冊：機率

🌍 機率的故事：從賭桌到科學

機率的起源，其實與賭博密不可分。

17 世紀的歐洲，貴族間流行各種骰子與牌類遊戲，
一位法國貴族在賭博中輸了不少錢，便向數學家布萊茲·帕斯卡（Blaise Pascal）求助。

帕斯卡與另一位數學家費馬（Pierre de Fermat）開始書信往返，
探討骰子遊戲的公平性與預測方法，這段對話也成為機率論的濫觴。

這門學問從賭桌起步，後來影響遍及各領域：保險、統計、經濟學、遺傳學、AI與大數據。

如今的天氣預報、Google 搜尋排序、疫苗研發，背後都藏有機率模型的影子。

🧠 為什麼要學機率？

因為人生充滿不確定，而機率就是用來理解與掌握「不確定性」的工具。

在高中數學中，機率的重點不僅是計算，更是思考：

我有哪些可能的情況？
這些情況哪個比較可能發生？
如何避免錯誤推論或直覺誤判？

🎲 接下來的題目

現在，讓我們來看一題融合機率觀念與動態思考的題目。

這不僅是數學演練，更是一場小小的策略遊戲。

我們要追蹤石子在圓上的移動，找出它恰好繞兩圈才回到原點的機率。

在解題之前，記得我們說的：

「先看清楚題目，就像抬頭看路標。」

《問題敘述》

一圓周上有六個等分點按順時針順序依次記為 \(A\)、\(B\)、\(C\)、\(D\)、\(E\)、\(F\)。

考慮如下遊戲：

開始時將一石子放在出發點 \(A\)，今投擲一骰子，若擲出偶數點，

則石子順時針前進兩個等分點；若出現奇數點，則石子順時針前進一個等分點。

當石子恰好停在 \(A\) 點時，則遊戲結束。

試問遊戲結束時，石子恰繞圓兩圈的機率為多少？

➤ 題意釐清（看路標）

圓上 6 等分：\(A→B→C→D→E→F→A…\)

每次擲骰：

奇數：前進 1 格
偶數：前進 2 格
兩者機率皆 \(\frac{1}{2}\)

遊戲在石子第一次回到 \(A\) 就結束
（第一次回到 \(A\) 的總前進步數一定是 \(6\)、\(12\)、\(18\)… 的其中一個）。

問：第一次回到 \(A\) 剛好是「兩圈」= 前進總步數 \(12\) 的機率。

關鍵：我們要的事件是「第一次回到 \(A\) 在 12，而不是先在 6 回到 \(A\)，
也不能在 12 前就回到 \(A\)」。

換句話說，要避開 6，但在 12 命中。

➤ 解題策略（怎麼做、為什麼）

石子前進路徑：\(A→F→B→A\) 

其中各路線擲骰子的可能情況

\(A→F\)：2偶1奇、1偶3奇、5奇

\(F→B\)：1偶

\(B→A\)：2偶1奇、1偶3奇、5奇

➤ 答案

$$所求機率 = [C^3_2 (\frac{1}{2})^3 + C^4_1 (\frac{1}{2})^4 + (\frac{1}{2})^5 ] \times \frac{1}{2} \times [C^3_2(\frac{1}{2})^3+C^4_1(\frac{1}{2})^4+(\frac{1}{2})^5]=\frac{441}{2048}$$

---

想要了解數學數位課程嗎？

➤ 詳情請見【自主學習式線上課程彙整】學生可以隨時開始學習
➤ 1對1視訊遠距教學：客製化教學，效果最佳。
➤ 徵高中數學（學測數A）家教學生 ：為目標14~15級分設計的課程