我們在上一篇文章中，
以差分的方式，看出了「多項函數之連續整數的函數值的關係」，
並且發現了，這些函數值前的倍數竟然可以對應到巴斯卡三角形。
論證的過程中，用了一些恆等式，例如：
巴斯卡公式：$$C^m_i+C^{m}_{i-1}=C^{m+1}_i,\ 1\leq i\leq m$$ 此公式可以直接以代數運算或組合觀點驗證，課本中已有詳細介紹。
還可以利用巴斯卡公式，推得級數和公式：
$$\begin{aligned}
1+2+3+…+n &= C^1_1+C^2_1+C^3_1+…+C^n_1 \\
&= C^2_0+C^2_1+C^3_2+…+C^n_{n-1}\\
&= C^{n+1}_{n-1}=C^{n+1}_2=\frac{(n+1)\cdot n}{2}
\end{aligned}$$
再稍微複雜一點，也可以推得平方級數和公式：設
$$\begin{aligned}
k^2 &= aC^k_2+bC^k_1 \\
&= a\cdot \frac{k(k-1)}{2}+b\cdot k \\
&= \frac{a}{2}k^2+(b-\frac{a}{2})k
\end{aligned}$$ 比較係數可得 \(a=2, b=1\)，因此 $$k^2=2\cdot C^k_2+1\cdot C^k_1, k\geq 2$$ $$\begin{aligned}
1^2+2^2+3^2+…+n^2 &= (2C^1_2+C^1_1) + (2C^2_2+C^2_1) + (2C^3_2 +C^3_1) + …+(2C^n_2+C^n_1) \\
&= 2\times (C^1_2+C^2_2+C^3_2+…+C^n_2) + (C^1_1+C^2_1+C^3_1+…+C^n_1) \\
&= 2\times C^{n+1}_{n-2}+\frac{n(n+2)}{2}=2\cdot C^{n+1}_3+\frac{n(n+1)}{2} \\
&= 2\times \frac{(n+1)\cdot n\cdot (n-1)}{3}+\frac{n(n+1)}{2}\\
&= n(n+1)[\frac{n-1}{3}+\frac{1}{2}]\\
&=n(n+1)\cdot\frac{2n+1}{6}=\frac{n(n+1)(2n+1)}{6}
\end{aligned}$$ 這個證明簡潔清楚，如果你想知道更多平方級數和公式的證明，
可參考另一篇文章：平方和公式的五個推導方式
另外，根據二項式定理，$$(1+x)^n=C^n_0 +C^n_1x+C^n_2x^2+…+C^n_nx^n$$ 可以代入不同的 \(x\) 值，得到不同的恆等式：
\(x=1\) 代入可得 $$C^n_0+C^n_1+C^n_2+…+C^n_n=2^n$$
\(x=-1\) 代入可得 $$C^n_0-C^n_1+C^n_2-…+(-1)^nC^n_n=0$$
\(x=2\) 代入可得 $$C^n_0+2C^n_1+2^2C^n_2+…+2^nC^n_n=3^n$$
這部份是課本的標準內容，同學們應該都很熟悉了。
接著，我們來看一些其他的變化：$$i\cdot C^{n}_i = n\cdot C^{n-1}_{i-1}\tag{1}$$
這個等式很容易驗證，藉由這個等式，可推導出以下恆等式$$C^n_1+2 C^n_2+3 C^n_3+…+n C^n_n = n\cdot 2^{n-1}$$ 運用第(1)式可得 $$左式=n\cdot (C^{n-1}_0+C^{n-1}_1+ C^{n-1}_2+…+ C^{n-1}_{n-1})=n\cdot 2^{n-1}$$ 再運用第(1)式可得 $$\frac{1}{n+1}C^{n+1}_i = \frac{1}{i} C^{n}_{i-1} \tag{*}$$
因此，$$\begin{aligned}
1+\frac{1}{2}C^n_1+\frac{1}{3}C^n_2+…+\frac{1}{n+1}C^n_n &= \frac{1}{n+1}(C^{n+1}_1+C^{n+2}_2+…+C^{n+1}_{n+1}) \\
&=\frac{1}{n+1}(2^{n+1}-1)
\end{aligned}$$ 將上式微調，可得出以下恆等式：$$C^n_1-\frac{1}{2}C^n_2+\frac{1}{3}C^n_3+…+(-1)^{n-1}\frac{1}{n}C^n_n=1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n} \tag{2}$$
如何驗證上式？
如果使用微分會簡單許多，但是高一學生還沒學到，先用初等的方法。
首先，我們試著將各項拆解
在等號左式的部份，考慮第 \(i\) 項
$$\begin{aligned}
\frac{1}{i} C^n_i &= \frac{1}{i} [ C^{n-1}_i+C^{n-1}_{i-1}] \\
&= \frac{1}{i}C^{n-1}_i + \frac{1}{i}C^{n-1}_{i-1} \\
&= \frac{1}{i}C^{n-1}_i+ \frac{1}{n}C^n_i \\
&= \frac{1}{i}[C^{n-2}_i+C^{n-2}_{i-1}] + \frac{1}{n}C^n_i \\
&= \frac{1}{i}C^{n-2}_i+\frac{1}{i}C^{n-2}_{i-1}+\frac{1}{n}C^n_i \\
&= \frac{1}{i}C^{n-2}_i+\frac{1}{n-1}C^{n-1}_i+\frac{1}{n}C^n_i \\
&= …\\
&=\frac{1}{i}C^i_i+\frac{1}{i+1}C^{i+1}_i+\frac{1}{i+2}C^{i+2}_i+…+\frac{1}{n-1}C^{n-1}_i+\frac{1}{n}C^n_i \\
&=\sum_{j=0}^{n-i} C^{n-j}_i \frac{1}{n-j}
\end{aligned}$$故
$$
左式 = \sum_{i=1}^n (-1)^{i+1}\frac{1}{i}C^n_i = \sum_{i=1}^n (-1)^{i+1}[\sum_{j=0}^{n-i}C^{n-j}_i\frac{1}{n-j}] \tag{3}
$$ 交換求和順序
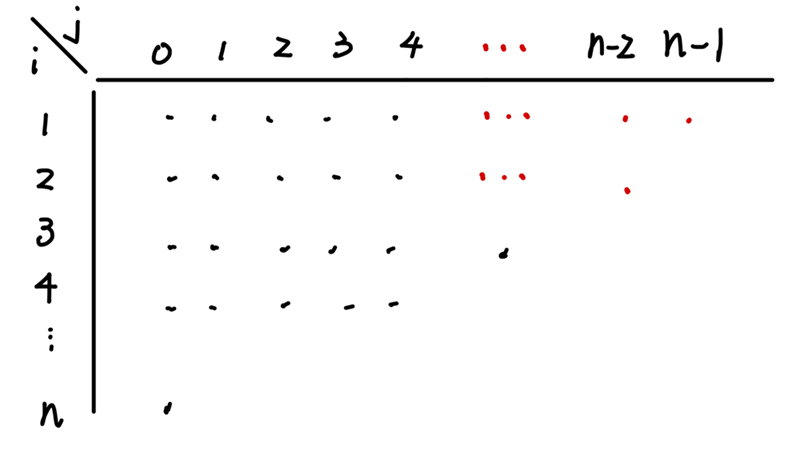
$$(3) = \sum_{j=0}^{n-1}\sum_{i=1}^{n-j}(-1)^{i+1}C^{n-j}_i\frac{1}{n-j}\tag{4}$$
令 \(k=n-j\)，則 $$(4)=\sum_{k=1}^n\frac{1}{k} \sum_{i=1}^k(-1)^{i+1}C^k_i = \sum_{k=1}^n \frac{1}{k} \ \ \ 得證$$
最後我們用微積分寫一次(驗證第(2)式)
先由二項式定理，寫出 \((1-x)^n\) 的展開式：$$(1-x)^n = C^n_0 -C^n_1 x + C^n_2 x^2 +…+(-1)^n C^n_n x^n $$ 上式減 \(1\) 再變號：
$$1-(1-x)^n =C^n_1 x -C ^n_2x^2+C^n_3x^3-+…+(-1)^{n+1}C^n_nx^{n}$$ 接下來等號兩邊同時除以 \(x\) 再積分：
$$\int_0^1\frac{1-(1-x)^n}{x}dx=C^n_1-\frac{1}{2}C^n_2+\frac{1}{3}C^n_3-…+(-1)^{n+1}\frac{1}{n}C^n_n\tag{5}$$
接下來要處理第(5)式等號左邊的積分，先將變數變換：令 \(1-x=\)，則積分形式可改寫
$$\begin{aligned}
\int_0^1\frac{1-(1-x)^n}{x}dx &= \int_0^1\frac{1-y^n}{1-y}dy \\
&=\int_0^1\frac{(1-y)(1+y+y^2+…+y^{n-1})}{1-y}dy \\
&=1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}\end{aligned}$$ 第(2)式成立。
這邊文章就先到這裡，提供學生補充學習。
歡迎訂閱高中數學數位學習電子報，我會在每週寄1~2封信，
與你分享學習數學的心得與方法，同時告知線上數學課的開課資訊。
No comments! Be the first commenter?