試題下載、參考答案 ▋整體命題趨勢與考科定位 114年分科測驗的數甲考題,整體風格可以用一句話總結:比重往高年..
不是學歷決定未來,而是你是否擁有一門無法被取代的技能
每年到了這個時節,許多家庭都開始討論升學的選擇:到底要念高中還是高職比較好? 這個問題沒有標準答案。 可是,我..
Podcast《用聽的學數學》
🎧 Podcast《用聽的學數學》第28集上線囉! 每天只要花十分鐘左右,就能培養數學思維 用聽的學數學,是課..
創造須要一點疏離感:你也有那個偷偷堅持的「祕密項目」嗎?
你是否聽過張益唐的故事? 他是一位傳奇的華裔數學家,其故事充滿堅毅與智慧,特別激勵著所有熱愛數學、但在現實中遇..
如何運用分式積分、變數變換求正割函數的積分?
早在17世紀,牛頓(Isaac Newton)與他的老師巴羅(Isaac Barrow)就已經開始思考一個深刻..
從最大公因數開始:理解中學數學與大學數學的本質差異
很多人在中學時數學成績優異,但一進入大學,卻彷彿踏入全然不同的世界。 為什麼會這樣? 因為中學數學強調的是直觀..
「明明是實數解,為什麼要經過虛數世界?」— 卡丹諾的驚訝與複數的誕生
國中時,我們學的所有數,無論是整數、分數、根數、圓周率…都是實數。但是,有一種數,卻在我們的實數世界中「找不到..
會考準備不焦慮:9個學生必懂的考前調整與得分技巧
會考是壓力,也是機會 國中會考,是許多學生人生中的第一場大型考試。 它不只是考你會不會,還考你穩不穩、撐不撐得..
正確的學習方法,只有一種風格
學習效果好的人,他們的學習方法都是相似的,學習效果不好的人,則各有各的學習方法。 那麼什麼才是有效的學習方法?..
不是老師沒教你不會,是你習慣等老師教
👉 其實你不是沒能力,而是缺了「主動學習」這個習慣。 「老師還沒教,所以我不會。」 這句話是不是聽起來很熟悉?..
三種驚人的休息方式
#閱讀:讓天賦自由的內在動力#個人經驗詮釋 做白日夢、靜坐、睡眠都能讓大腦休息。 尤其睡眠充足對現代人的生活格..
對付拖延的五個訣竅
寫作業是學習數理的重要步驟之一, 為什麼有些學生總是無法按時完成作業? 其實,這不一定是因為「懶惰」,而是「拖..
新手學生攻略:如何使用ipad學數學?
一在iPad上的數學教育 工欲善其事,必先利其器! 學數學不再侷限於紙本筆記,iPad是強大的學習工具,正確使..
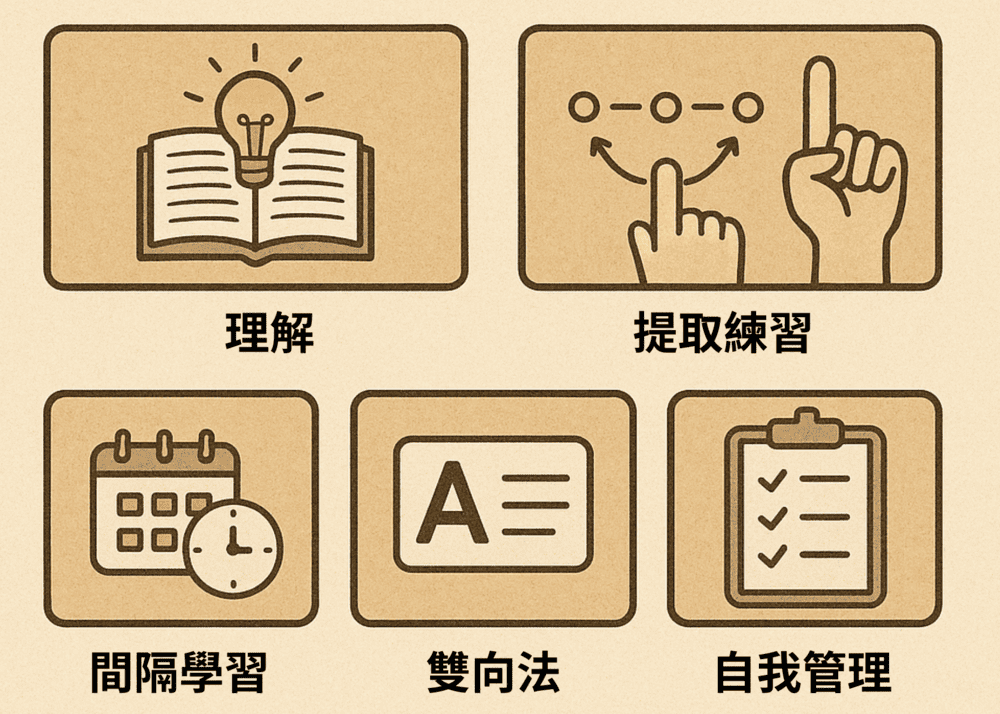
學習如何學習:有效學習的五個策略
教學的過程中,我發現,很多學生不是不願意努力, 而是找不到學習方法,或是用錯誤的方法學習。 造成的結果就是,耗..
個案分析:為什麼作業已寫完並且還額外寫資優試題,成績表現仍不理想?
方便請教老師孩子數學學習上的一個盲點嗎? 孩子在校麻辣講義均有落實完成,甚至也寫了資優A++, 但此次期末考數..