數學觀念補給站

學習數學應該包含一些記憶和大量的理解，順序弄反，結局大不同。
換句話說，即使一字不漏地背下整本課本或是講義，也於事無補。

這就是為什麼，數學這門科目，會給一些學生造成困擾。
明明我都很認真讀書了，可是怎麼還是考不好？

追根究柢，很大一部份的原因就是，用了太多的記憶，太少的思考與推理所導致。

學習數學的確須要一些記憶，例如：題目問五邊形的對角線個數？
我們當然要先知道對角線的定義就是任一頂點，與其他非相鄰兩點的頂點相連的線段。
接著連連看，發現會有五條。

接著再問自己，六邊形會有幾條對角線呢？

在課堂上，有學生完全不假思索，立即回答六條。

是嗎？我們畫畫看。

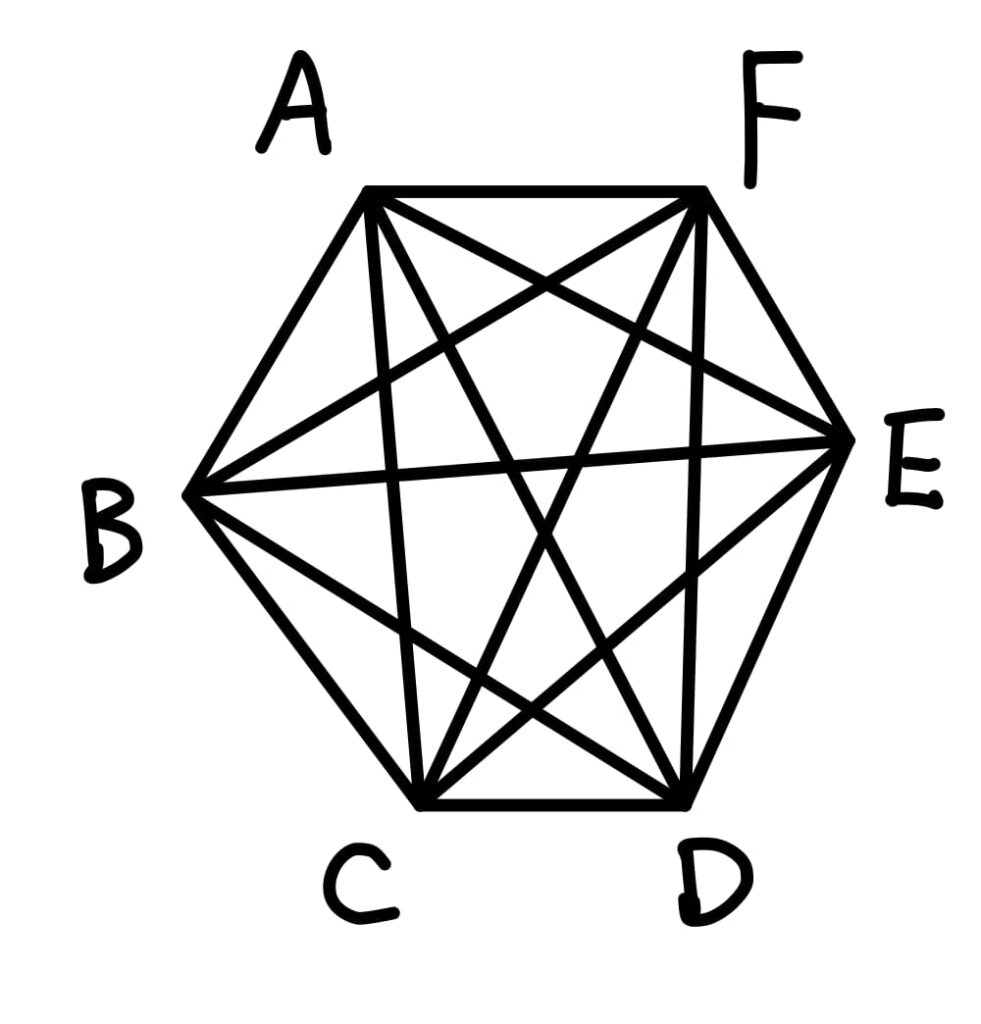
不對呀，應該有九條才對！

這時候就要好好思考，當初我們是如何確定五邊形的對角線個數？
如果每次都是慢慢畫，當邊數增加時該怎麼處理呢？

顯然這不是一個好的策略對吧！

所以學習數學的過程中，不要滿足於只是將答案算出來，
而是要多思考其中的道理是什麼。

如果出了100題計算多邊形對角線個數的題目，
而每一次我們都是慢慢畫出來。

你覺得這樣做完100題，數學能力會進步嗎？
我想答案是否定的！

很多學生學習數學就是這種模式，拚命用不對的方法刷一大堆題，
結果就是事倍功半。

數學是理科，要說道理。

換個思考方式，對於五邊形而言，每個頂點可以連出 \(2\) 條對角線，
那麼五個頂點，應該就能連出 \(5\times 2 = 10\) 條對角線，
好像哪裡怪怪的，我們沒有連出這麼多條呀。

對了，因為線段 \(\overline{AC}\) 及 線段 \(\overline{CA}\) 是同一條，我們多算了一次。
因此最後的答案要再除以 \(2\) 才對。

太好了，有了這樣的想法，管它幾邊形，都可以馬上破解。

六邊形的對角線個數為 \(6\times 3÷2=9\)
七邊形的對角線個數為 \(7\times 4÷2=14\)
八邊形的對角線個數為 \(8\times 5÷2=20\)

等等，好像有規則耶！

如果是 \(n\) 邊形，那麼對角線個數應該是多少呢？

按照以上規則可知，答案應該是 $$\frac{n(n-3)}{2}$$

我們再理解一次：\(n\) 邊形的每個頂點，扣除自己及相鄰兩點，可連接出 \(n-3\) 條對角線，因為有 \(n\) 個頂點，
所以會有 \(n\times (n-3)\) 條，但是要扣除重複算到的部份，因此再除以 \(2\)，最後就得出那個公式了！

原來，這就是我們所謂的公式，是可以慢慢被觀察出來的。
而不是一開始背起來，然後看到題目開始套公式。

這樣的學習方式，是不是有趣多了呢？

學習數學就是這樣，每學習一個新的單元，的確須要理解也須要一些記憶。

對於較深入的題型，則須要抽絲剝繭，慢慢推理。等到熟悉了，就會變成我們思維的一部份，
很多時候真的就可以不假思索，準確看到問題的本質。

一道好的問題，往往會有很多不同思考的角度與方向。

最近兩個月，我正在為高三學生上第二階段數學筆試的題目，
其中又以台大資工、電資學院的題目居多。

雖然有些題目我已經寫過了，但是隔了一陣子再回來看，
又有了不同的想法與觀點。甚至還發現了自己當初思考的盲點，
這也是與學生討論的過程中的收穫，教學相長就是這樣來的。

接下來，我們來聊聊以下這道挺有意思的題目。

以海龍公式證明不等式

設 \(a\)、\(b\)、\(c\) 為三正數滿足 \(a+b+c=3\)，試證：$$(3-2a)(3-2b)(3-2c)\leq a^2b^2c^2$$

這個不等式，看起來挺神奇的。為了方便討論，不失一般性，先假設 \(a\leq b\leq c\)。

如果左式為「非正數」，那麼此不等式明顯成立。因此我們的重點在於處理左式「非負」的情形。
為了讓論證過程清晰，選擇分類方式就格外重要。

首先先將情況分成兩大類：
情況1：$$a\leq b\leq \frac{3}{2}\leq c$$ 這個情況會造成左式非正，此不等式明顯成立。

情況2：$$a\leq b\leq c\leq\frac{3}{2}$$

想想看，是否還有其他情形呢？例如 \(a\leq\frac{3}{2}\leq b \leq c\)

這個情況不用考慮了，因為無法符合 \(a+b+c=1\)。同樣道理， \(\frac{3}{2}\leq a\leq b \leq c\) 也可以被排除了。

接著回到情況2：

情況2.1：\(a+b=c\)，此時可得 \(c=\frac{3}{2}\)，左式為 \(0\)，此不等式顯然成立。
情況2.2：\(a+b<c\)，則 \(c>\frac{3}{2}\)，造成矛盾，此情況不可能發生。
情況2.3：\(a+b>c\)，這個情況之下，\(a,b,c\) 可構成三角形的三邊長。

依照此不等式的形式，可聯想到三角形的面積公式與三邊長相乘及開根號的形式。
$$\frac{abc}{4R}=\Delta = \sqrt{\frac{3}{2}(\frac{3}{2}-a)(\frac{3}{2}-b)(\frac{3}{2}-c)}\ \ \ (海龍公式) \tag{1}$$

重點來了，那個外接圓半徑必須估計一下範圍。

由正弦定理可知，$$a=2RsinA, \ b=2RsinB, \ c=2RsinC$$

因此，$$3=a+b+c=2R(sinA+sinB+sinC) \tag{2}$$

此時衍生出另一個問題，\(sinA+sinB+sinC\) 的極值是多少呢？

大膽猜測，當此三角形為正三角形時，\(sinA+sinB+sinC\) 會達最大值為 \(\frac{3}{2}\sqrt{3}\)

但是要如何證明呢？

可以利用正弦函數凹口向下的特性得出以下不等式：$$\frac{sinA+sinB+sinC}{3}\leq sin{\frac{A+B+C}{3}}=sin{\frac{\pi}{3}}=\frac{\sqrt{3}}{2}$$

回到第 (2) 式可得$$3\leq 2R\cdot \frac{3}{2}\sqrt{3}$$ 兩邊同時除以\(\sqrt{3}\) $$R\geq\frac{1}{\sqrt{3}}$$

接著再回到第(1)式，將不等式兩邊平方可得 $$\frac{3}{16}a^2b^2c^2 \geq \frac{3}{16}(3-2a)(3-2b)(3-2c)$$
不等式兩邊同時除以 \(\frac{3}{16}abc\) 可得：$$(3-2a)(3-2b)(3-2c)\leq a^2b^2c^2$$

由以上論證，可以衍生以下三個問題：

問題1： 在 \(\Delta ABC\) 中，\(cosA+cosB+cosC\)之最大值為何？

問題2：在銳角 \(\Delta ABC\) 中，\(tanA+tanB+tanC\)之最小值為何？

問題3：在銳角 \(\Delta ABC\) 中，\(cotA+cotB+cotC\)之最小值為何？

這三個問題，讀者不妨想想，我在下一篇文章再來解答喔。

---

---

歡迎訂閱 高中數學數位學習電子報