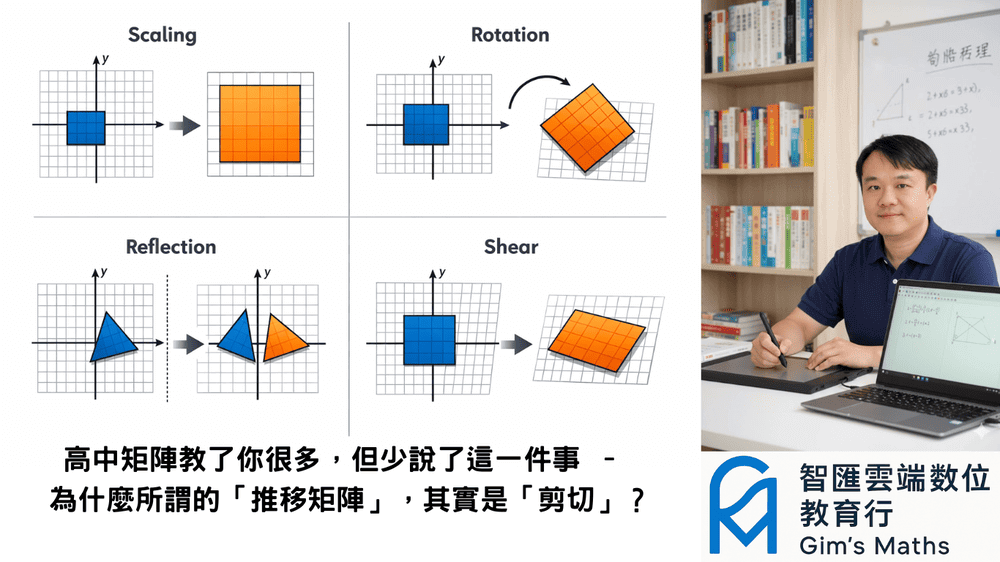
高中數學第四冊,關於平面上的線性變換,我們學到了旋轉、鏡射、伸縮、推移。 為什麼我們要了解這四種矩陣? 原因是..
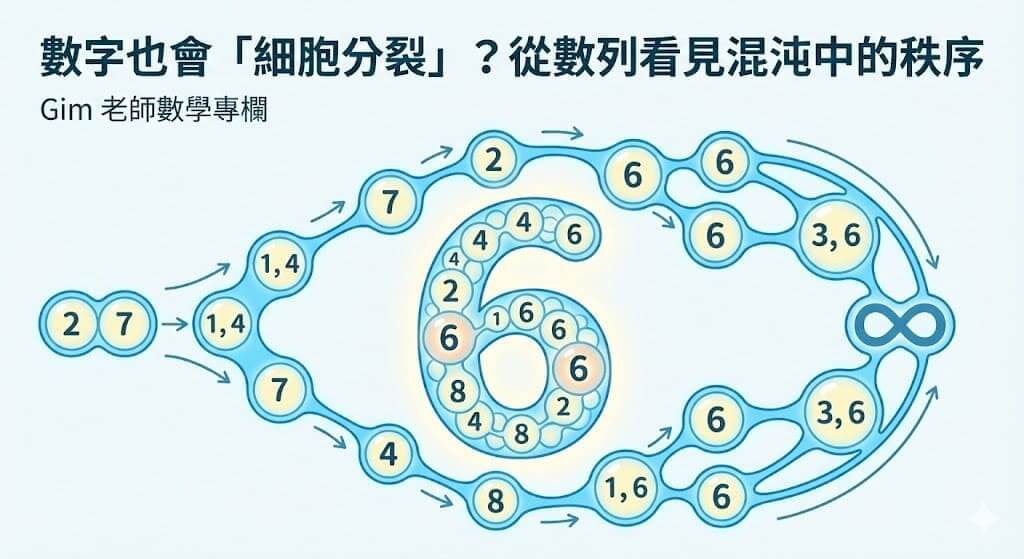
數學專欄:數字也會「細胞分裂」?從數列看見混沌中的秩序
在高中數學的數列章節中,我們習慣了等差、等比這些規律整齊的數列。但在數學競賽或更高等的動力系統理論中,有一類數..
當艾力克斯徒手攀上 101:學習,其實就是一場「心智的徒手獨攀」
2026 年 1 月 25 日,全球的目光都聚焦在台北。 傳奇攀岩家艾力克斯·霍諾德(Alex Honnold..
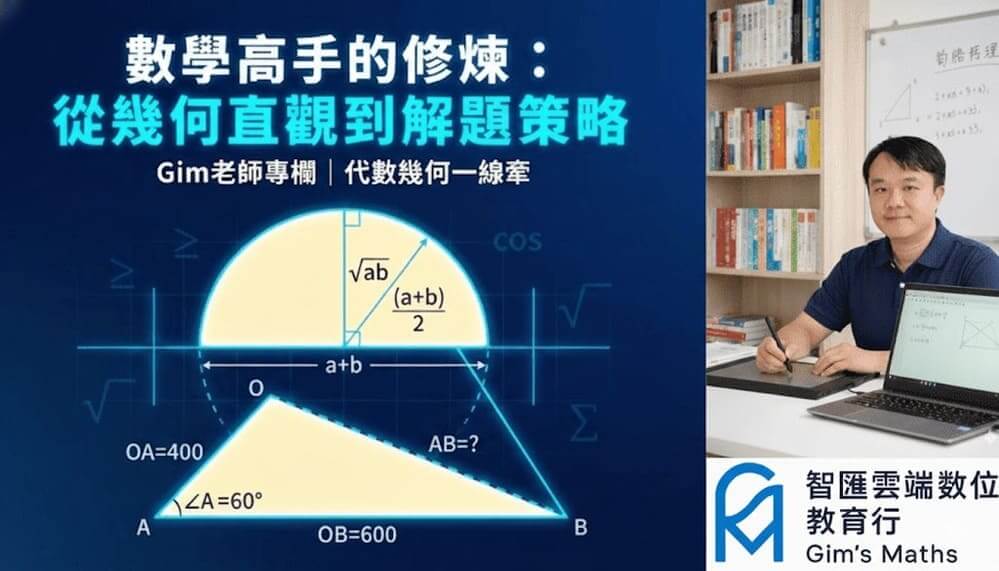
【Gim 老師數學專欄】從「算對」到「會想」:數學高手的五階段修煉之路
在高中數學的戰場上,很多同學就像裝備精良的士兵,背滿了公式(武器),但在戰場上卻不知道該拔哪一把劍。 根據筆者..
115年學測數a第20題:已知面,求體積?用向量「逆向工程」解構平行六面體的秘密;多選8~12題;選填13~17題影片解說。
前言:從「黑盒子」看幾何:115年學測數a第20題 在立體幾何的學習中,我們通常習慣「順向操作」:給你三個邊長..
當總和固定,乘積為什麼會選擇 3?——從一題經典整數問題,看見「結構」
前言:當數字大到無法直觀時 在解決複雜問題時,我們常會感到無從下手。本週要探討的這道經典試題,給了我們一個極佳..
【數學家的筆記】把「禁止」變成「動力」:帕斯卡教你的三堂逆境學習課
今天我們要聊一位 17 世紀的數學家——布萊斯·帕斯卡(Blaise Pascal)。 你可能在物理課聽過「帕..
別急著代公式!畫出正弦波,不等式就在圖形裡
在高中數學處理三角不等式時,很多同學的直覺反應是打開和差化積公式,或者試圖展開運算。 但今天我們要暫時放下代數..
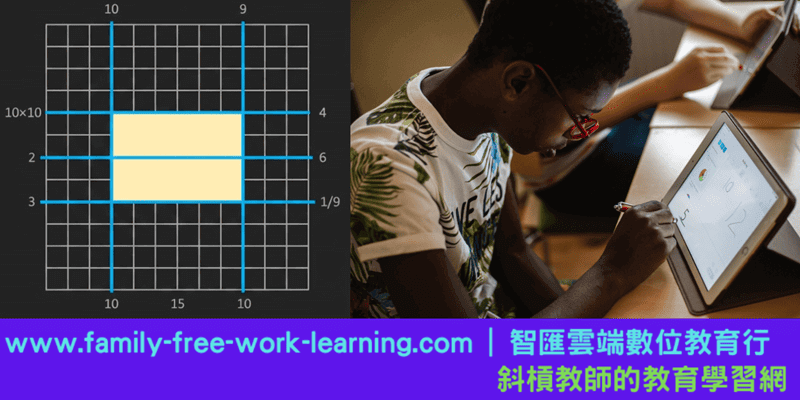
為什麼在格子紙上隨機畫一個矩形,平均面積總是佔整體的九分之一?
「如果你手邊有一張 \(n \times n\) 的格子紙,閉上眼睛,隨手選出四條線圍成一個矩形。這個矩形可能..
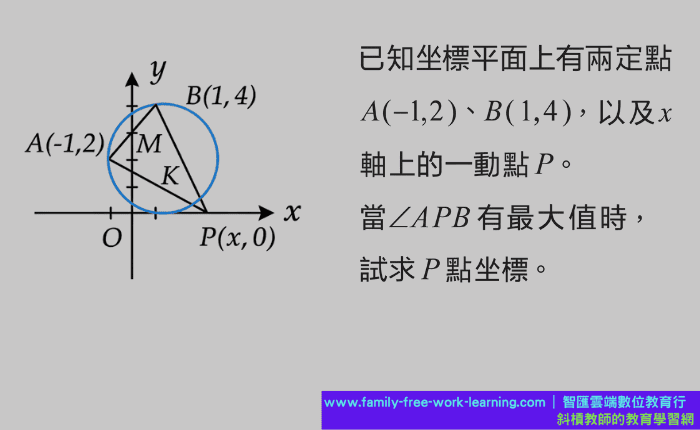
凝視的幾何學:當數學家站在畫作前
試著想像這樣一個場景:你站在美術館的一幅巨型畫作前。 這幅畫懸掛在高處,底端離地一段距離。 如果站得太遠,畫作..
適當的座標化,可有效簡化問題:迪卡兒的化繁為簡之道
提到迪卡兒,大多數人的第一反應可能是那句響徹哲學史的名言:「我思,故我在」(Cogito, ergo sum)..
從一道看似困難的極限題,認識 Taylor 級數:一個改變科學的偉大想法
在高三的選修數學裡,我們學到了一些處理極限的方法:例如 有理化分母、通分化簡、利用三角恆等式、指數與對數的轉換..
穿越 19 世紀:柯西如何寫下改變數學史的經典不等式?
如果你走進 1820 年左右的巴黎科學院,你可能會覺得自己像誤入現代的某個 Reddit 辯論版:每位數學家都..
不只是算位置:一題教你看懂排列組合的思考方式
在所有高中數學單元裡,「排列組合與機率」大概是最容易讓人一頭霧水的主題之一。 教書二十多年來,我發現有不少學生..
從一條神祕的數列,談「遞迴」的魔法
這週,高中數學第二冊,我們進入到了數列的世界。學生上課時問說,數列好像只是一直在做計算,有什麼特別的意義嗎?為..