在高中數學的戰場上,很多同學就像裝備精良的士兵,
背滿了公式(武器),但在戰場上卻不知道該拔哪一把劍。
根據筆者對數學學習法的深度剖析與25年的教學經驗,
與你分享:學好數學不只是「算得快」,
更是一場關於「思考結構」的升級遊戲。
今天,我將這套系統歸納為五個修煉階段,
帶你從「背誦者」進化為「策略家」。
1. 建立基本的解題策略與思維
什麼是解題策略?
簡單來說,就是當你面對一個題目時,主動發現思考方向的能力 。
很多同學遇到沒見過的題目就束手無策,是因為他們習慣「記題目」,而不是「思考題目」 。
基本的解題策略,第一步就是將文字敘述進行 「數學化」 的翻譯工作 。
- 翻譯已知與求解:例如看到「求直線方程式」,馬上聯想到設 \( y = ax + b \) 或 \( mx – y = k\)。
- 建立連結:解題的本質,就是找出「已知條件」與「所求目標」之間的關係 。
當你看不出直接關係時,不要慌。
試著問自己:「這題屬於哪個單元?有哪些定理可以用?」 。
例如看到三角形邊角問題,自然聯想到正弦或餘弦定理;
看到極值問題,聯想到配方法或算幾不等式 。
這就是最基礎的策略思維。
2. 熟練基本運算與原理的內化
有了策略,還需要扎實的基本功。
基本運算必須練到 「自動化」 的程度 。
為什麼要自動化?
因為當你的大腦不需要為了「移項」或「通分」這類瑣事消耗能量時,
你才能騰出空間去處理更高階的邏輯思考 。
但請注意,「熟練」不等於「死背」。
你必須對定義與定理有 百分之百的理解 。
舉個例子,很多學生會背 \( \sqrt{a} \times \sqrt{b} = \sqrt{ab} \),卻不知道為什麼。
結果考試時就容易犯下 \( \sqrt{2} + \sqrt{3} = \sqrt{5} \) 這種嚴重的錯誤 。
正確的學習方式是,要能自己重新推導一次原理,並且說出自己的理解。
就像學習 餘式定理 時,不要只記結果 \( f(c) = r \),
要知道如何使用除法原理推導,並且說出求函數值與求餘式之間的關聯。
只有理解了原理,面對變形題時你才不會慌。
3. 提升對標準題的理解層次
做完題目看解答,你都怎麼看?
這裡提供「理解的四個層次」,這也是區分高手與普通學生的分水嶺:
- 第一層:看懂解答(知道這一步是做什麼)。
- 第二層:為什麼這樣做是對的?(確認邏輯的合理性) 。
- 第三層:為什麼會想到要這樣做?(這是最關鍵的一步!) 。
- 第四層:這一類的問題該怎麼做?(歸納出通用的策略) 。
很多同學停留在第一層,覺得看懂就等於會了。
但真正的學習發生在第三層。
例如在解 算幾不等式 時,不要只看懂算式,
要問自己:「為什麼這題要用算幾而不是配方法?」
答案往往藏在題目結構裡——因為你看到了「特殊結構」而產生聯想。
4. 構築從小範圍到大範圍的解題策略
策略不是零散的,而是像積木一樣堆疊的。
- 小範圍策略:這是針對特定條件的反射動作。
例如看到「圓內接四邊形」,馬上想到「對角互補」 。 - 大範圍策略:這是將多個小策略組合起來的系統。
例如「解三角形」這個大策略,其實就是整合了正弦定理、
餘弦定理與內角和性質 。
這就像一位精通特定角色的電競選手轉練新角色,
他會先沿用原本的走位與地圖觀(小策略),
再針對新角色的技能特性進行微調,最終融會貫通,
練就出一套對戰局的全面掌控力(大策略)。
當你建立了自己的大範圍策略庫,面對綜合題時,
你就不再是亂槍打鳥,而是有條理地調用工具 。
5. 策略的實戰演練:以三角、指數與不等式為例
最後,讓我們用兩個實戰範例,展示策略是如何在 代數 與 幾何 中靈活運用的。
你會發現,核心都在於「辨識結構」。
【代數戰場:算幾不等式】
情境:物流中心模型成本為 \( f(x) = 4x + \frac{9}{x} \)(\( x>0 \)),求最低成本。
策略修正: 一般我們求極小值會想用配方法,但這裡變數在分母。
目標:「求最小值,找相乘為定值」 。
檢查結構:\( 4x \times \frac{9}{x} = 36 \)(定值)。
策略啟動:直接使用算幾不等式 \( \frac{4x + 9/x}{2} \ge \sqrt{36} \),秒殺問題。
這顯示了策略如何從簡單的「正數」條件擴充到處理「定值結構」 。
【幾何戰場:三角導航】
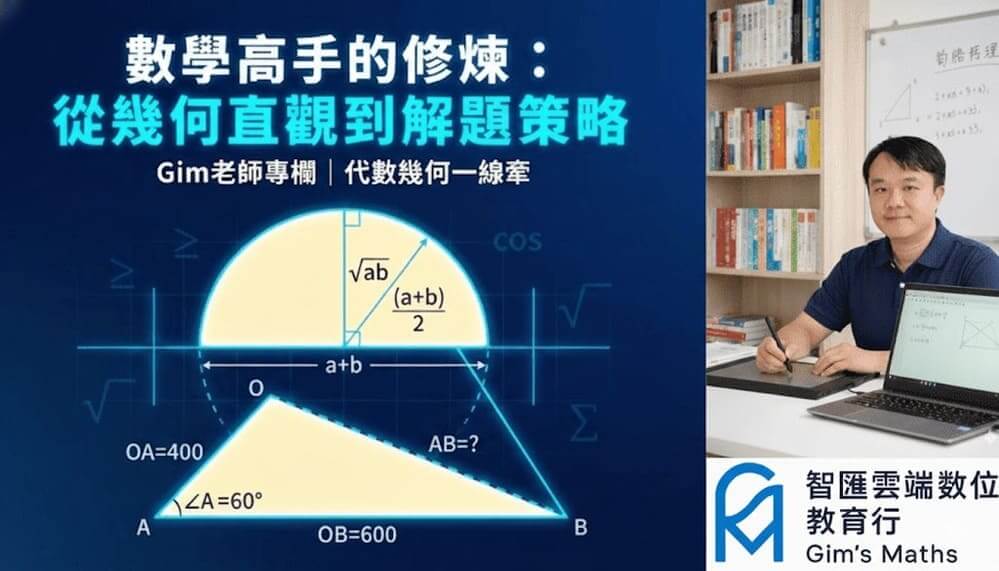
情境:無人機搜救,已知兩邊 \( \overline{OA}=400, \overline{OB}=600 \) 與夾角 \( \angle O=60^\circ \),求距離 \( \overline{AB} \)。
策略選擇:
面對三角形,我們有兩把劍:正弦與餘弦。
依據策略庫:
- 正弦定理:需要「成對」的邊角關係 。
- 餘弦定理:處理「夾擠」(兩邊一夾角)或「三邊」關係 。
本題結構為 SAS(夾擠),因此毫不猶豫選擇 餘弦定理 \( c^2 = a^2 + b^2 – 2ab \cos C \) 。
總結:
從代數的「定值結構」到幾何的「夾擠結構」,
學好數學的過程,就是建立這套屬於你的導航系統。
當你不再背題目,而是開始分析結構時,
你就真正走在正確學習數學的路上了。