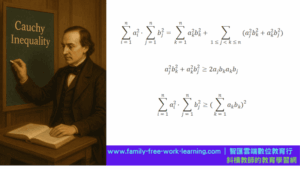數學教育

如果你走進 1820 年左右的巴黎科學院，你可能會覺得自己像誤入現代的某個 Reddit 辯論版：
每位數學家都脾氣火爆、意見極強、堅持己見。
算式會吵、定義會吵、連「你這樣寫算不算證明」都可以吵上一整年。

而在這群大佬之間，有一位安靜卻固執的年輕人，他叫——柯西（Augustin-Louis Cauchy）。

他不是天才。
至少同時代的數學家不這麼認為。

有人覺得他太「古板」，
有人說他「不懂變通」。
甚至有人嘲笑他：「你每天只是在那裡鑽牛角尖。」

但這個年輕人心裡很清楚：
數學要真正「站得起來」，必須建立在紮紮實實的基礎上。

1.一個不靠天份、只靠紀律的人

當時的巴黎，正處於拿破崙時代後的混亂轉型期。
科學院裡的巨頭——拉格朗日（Lagrange）與拉普拉斯（Laplace），都已經是「傳說人物」。

但在這個時代的學術環境裡，證明常常是「憑直覺」、「憑圖形」、「大概就是如此」。
你在課本中看到的那種 ε-δ 嚴謹證明？
在那之前根本沒人當一回事。

而這就是柯西看不下去的地方。

別人靠天份寫文章，他靠紀律與細節。
每天固定工作、固定演算、固定閱讀，他甚至因為太過拘謹而被同事戲稱：

「整個分析學界的整理師傅。」

但他不在意。
他知道自己正在做的是一件 會改變數學史的事。

2.柯西的使命：整頓微積分世界

在那個年代，你如果問十個數學家：「極限是什麼？」
大概會得到十種答案，甚至有人會露出詭異的自信微笑，然後開始畫奇怪的曲線。

柯西決定「全部重寫」。

1821 年，他出版了劃時代的《分析教學》（Cours d’Analyse），其中包含：

✔ 極限的第一個嚴謹定義
✔ 連續的現代定義
✔ 導數與積分的真正邏輯
✔ 無窮級數收斂的規範
✔ 以及，後世稱為——柯西不等式（Cauchy Inequality）

那時候的他，才 32 歲。

很多人以為柯西不等式是用來算高中題目的。
事實上不然——
它原本是柯西研究無窮級數時的一個重要工具。

他想回答一個關鍵問題：

「什麼條件下，一個無窮級數真的會收斂？」

於是柯西找出了向量之間的深層關係，提出了那個影響百年的不等式。

3.耿直的個性：跟大佬槓上也不退縮

你以為柯西的故事是一個乖孩子努力成功的故事嗎？

不。

他脾氣非常硬。

✔ 他跟拉格朗日爭論過「什麼才算極限」
✔ 他被老一輩數學家批評「太過形式化」
✔ 他因為宗教立場得罪政治人物，錯失講座
✔ 他甚至被學生組織抗議過（因為太嚴格）

但這些衝突並沒有讓他放棄。
反而讓他的信念更加堅定：

「數學應該是清楚的、精確的、站得住腳的。」

也因為他的固執，後來整個微積分變得前所未有地安全、可靠、邏輯通順。

你今天在課本看到：

  • 柯西不等式
  • 柯西序列（Cauchy sequence）
  • 柯西積分
  • 柯西問題
  • 柯西條件……

並不是因為他喜歡把自己的名字貼 everywhere。
而是因為他真的改寫了一整個學科的地基。

4.柯西不等式：不是「額外公式」，而是思想的縮影

當你在算：

(a1b1+a2b2+...+anbn)2≤(a12+a22+...+an2)(b12+b22+...+bn2)\Large (a_{1}b_{1}+a_{2}b_{2}+…+a_{n}b_{n})^{2}\le (a_{1}^{2}+a_{2}^{2}+…+a_{n}^{2})(b_{1}^{2}+b_{2}^{2}+…+b_{n}^{2})

你可能會覺得這只是一個看似複雜的技巧題。
但在 1821 年的柯西眼中，它代表的是：

「如何用邏輯，控制無窮級數的行為。」

這個不等式後來還成為向量內積的基礎形式，
並且在傅立葉級數、微分方程、機率、線性代數、甚至機器學習中都有影響。

換句話說：

👉 你今天在課本裡看到的，是柯西在兩百年前為了「讓數學站得起來」所留下的工具。

在課堂上，我們通常採用內積的定義來證明：
利用向量的夾角範圍、法向量的長度，
就能很自然地得到這條在課本中看起來「威嚴」的不等式。

但如果我們把時間調回到 1821 年，
柯西當時可沒有你現在擁有的這些向量工具。
甚至——向量的代數形式還沒有被正式發明。

那麼，他是怎麼想到這個不等式的？

這正是這篇文章要帶同學延伸的地方。

5.柯西不等式的多種證明（從課本到數學史的橋樑）

為了讓無窮級數的研究更有「可控性」，
柯西開始思考：
如果兩串數列互相相乘後加總，
有沒有一種「上界」可以約束它的大小？

於是，他用的其實是一個非常原始卻深刻的觀念：

凡是平方，都不可能是負的。

這個最基本的事實，放到莖莖細細的代數結構裡，
反而成了柯西不等式的第一個雛形。

因此除了向量內積的證法，
另外介紹兩種有趣、也非常經典的證明方式：

① 利用平方恆為非負的證法（最接近柯西本人當年的思路）

考慮一個 \(x\) 的二次函數

f(x)=∑i=1n(aix−bi)2\Large f(x)=\sum_{i=1}^{n}(a_ix-b_i)^2

展開得

f(x)=(∑i=1nai2)x2−2(∑i=1naibi)x+∑i=1nbi2\Large \Large f(x)=(\sum_{i=1}^{n}a_i^2)x^2-2(\sum_{i=1}^{n}a_ib_i)x+\sum_{i=1}^{n}b_i^2

因為它永遠不會小於 0，且二次係數為正，因此判別式 \(D \leq 0\)

D4≤0⟹(∑i=1naibi)2−(∑i=1nai2)(∑i=1nbi2)≤0\Large \frac{D}{4}\le 0 \Longrightarrow (\sum_{i=1}^{n}a_ib_i)^2-(\sum_{i=1}^{n}a_i^2)(\sum_{i=1}^{n}b_i^2)\le 0

移項整理，柯西不等式就跑出來了。
這個證法非常漂亮，
它把一個「不等式」變成「拋物線開口向上」的圖形概念。

寫不等式時，要留意等號成立的條件：\(D=0\)

此時，存在唯一一個實數 \(x_0\) 使得 $$f(x_0)=0$$ 故

aix0−bi=0,1≤i≤n\Large a_ix_0-b_i=0, 1\leq i \leq n

也就是說

a1b1=a2b2=...=anbn\Large \frac{a_1}{b_1}=\frac{a_2}{b_2}=…=\frac{a_n}{b_n}

我們來看另一種寫法——只需要你國中學過的平方公式：

(x−y)2≥0\Large (x-y)^2\ge 0

把這個想法搬到多項的情形下，就會得到：

(a1​b2​−a2​b1​)2≥0\Large (a_1​b_2​−a_2​b_1​)^2≥0

試看看吧：

∑i=1nai2⋅∑j=1nbj2=∑k=1nak2bk2+∑1≤j<k≤n(aj2bk2+ak2bj2)\Large \sum_{i=1}^{n}a_{i}^{2}\cdot\sum_{j=1}^{n}b_{j}^{2} =\sum_{k=1}^{n}a_{k}^{2}b_{k}^{2}+\sum_{1\leq j< k \leq n}(a_{j}^{2}b_{k}^{2}+a_{k}^{2}b_{j}^{2})

因為

aj2bk2+ak2bj2≥2ajbkakbj\Large a_{j}^{2}b_{k}^{2}+a_{k}^{2}b_{j}^{2}\geq 2a_{j}b_{k}a_{k}b_{j}

所以

∑i=1nai2⋅∑j=1nbj2≥(∑k=1nakbk)2\Large \sum_{i=1}^{n}a_{i}^{2}\cdot\sum_{j=1}^{n}b_{j}^{2}\geq (\sum_{k=1}^{n}a_{k}b_{k})^{2}

接下來看等號成立的條件：設

a⇀=(a1,a2,...,an),b⇀=(b1,b2,...,bn),\Large \overset{\rightharpoonup }{a}=(a_{1},a_{2},…,a_{n}),\overset{\rightharpoonup }{b}=(b_{1},b_{2},…,b_{n}),

若

a⇀//b⇀\Large \overset{\rightharpoonup }{a}//\overset{\rightharpoonup }{b}

設

a⇀=λb⇀\Large \overset{\rightharpoonup }{a}=\lambda\overset{\rightharpoonup }{b}

則

∑i=1nai2⋅∑i=1nbi2=λ2(∑i=1nbi)2=(∑k=1nakbk)2\Large \sum_{i=1}^{n}a_{i}^{2}\cdot\sum_{i=1}^{n}b_{i}^{2}=\lambda^2(\sum_{i=1}^{n}b_{i})^2=(\sum_{k=1}^{n}a_kb_k)^{2}

等號成立

6. 想告訴學生的話：

柯西不是天才，但他寫下了天才們要用的基礎。

他不靠靈光一閃，而是靠：

  • 細膩
  • 嚴謹
  • 耐心
  • 固執
  • 以及「把事情做到最精準」的信念

才成為「現代數學分析之父」。

你現在在課本看到的每一條不等式、定義、條件，
很可能都有他的影子。

歡迎訂閱 高中數學數位學習電子報

高中數學數位學習電子報訪客

數學數位學習教室
國高中自主學習式線上課程


Author: Gim chen