課程目錄

第一章 二元一次聯立方程式

1-1 二元一次方程式
1-2 解二元一次聯立方程式
1-3 應用問題

第二章 直角座標與二元一次方程式的圖形

2-1 直角坐標平面

【補充教學】國中生如何理解用行列式求給定三頂點坐標的三角形面積？

最近七年級的課程，正在進行第二冊2-1直角坐標平面。當中有一道題目，給定一個三角形的三頂點坐標，要求出這個三角形的面積。

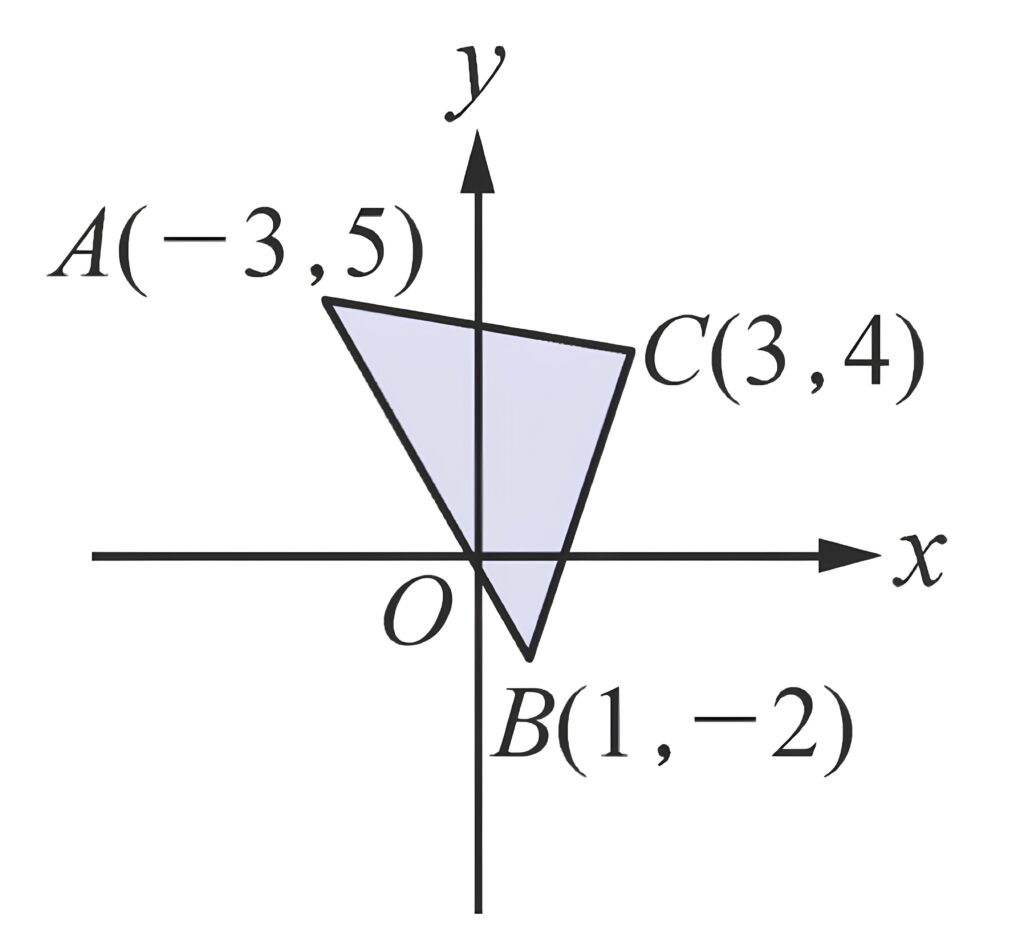
在國中階段，學生寫的題目大多以具體的數字計算為主，比較缺乏以符號推導公式的經驗，剛好藉著這個題目作為橋樑，相信有助於提升學生的思考層次。

這種題目，一般我們會選擇將圖形「切割」或是往外補成長方形再扣掉多餘的部份。這一個圖形不易切割，因此往外補是比較好的選擇。

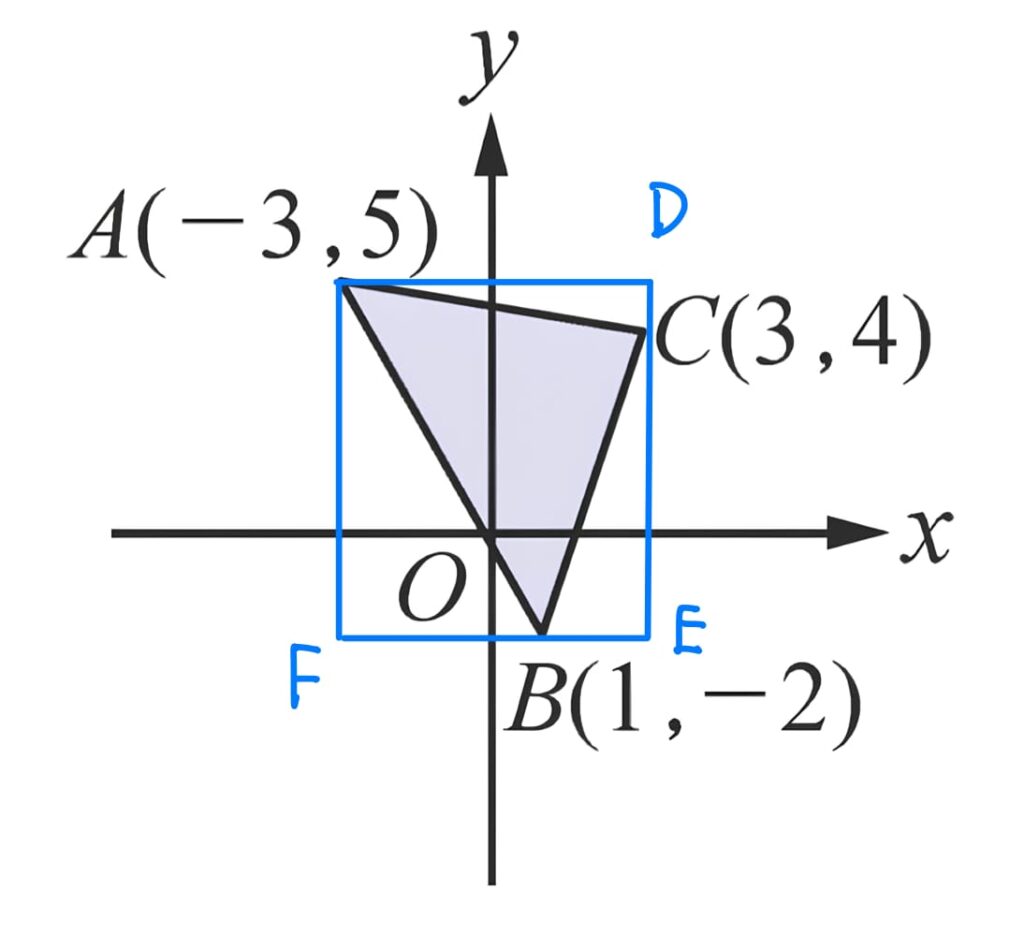
$$\begin{aligned}
\Delta ABC的面積 &=矩形AFED的面積 – \Delta ABF的面積 – \Delta BEC的面積 – \Delta ACD的面積 \\
&=7\times6 – \frac{1}{2}\times 4\times7 – \frac{1}{2}\times 2\times 6 – \frac{1}{2}\times 6 \times 1 \\
&= 19
\end{aligned}$$

接著有學生說，這樣做太麻煩，他在補習班有學到另一個方法，補習班老師說這個方法在寫計算題時不要使用，做法如下：

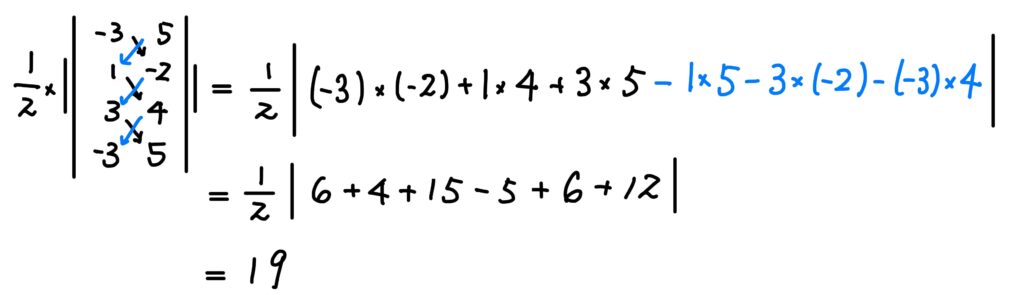
這個其實就是高中數學才會提到的行列式，沒有國中生知道可以這麼做的原因，然後就背下這個方法，遇到題目再套進去，考試時可以快速求得答案。然而，就以數學思維能力的提升而言，卻沒有任何幫助。因此，這一篇文章將進一步討論，這個公式是怎麼來的？

其實原因就藏在我們一開始，用矩形扣掉三個三角形的方法裡面。可是為什麼我們沒有看出來呢？

因為數字在運算過程中，被合併與消除了，導致我們看不出形式。因此改以符號表示，再觀察一下：

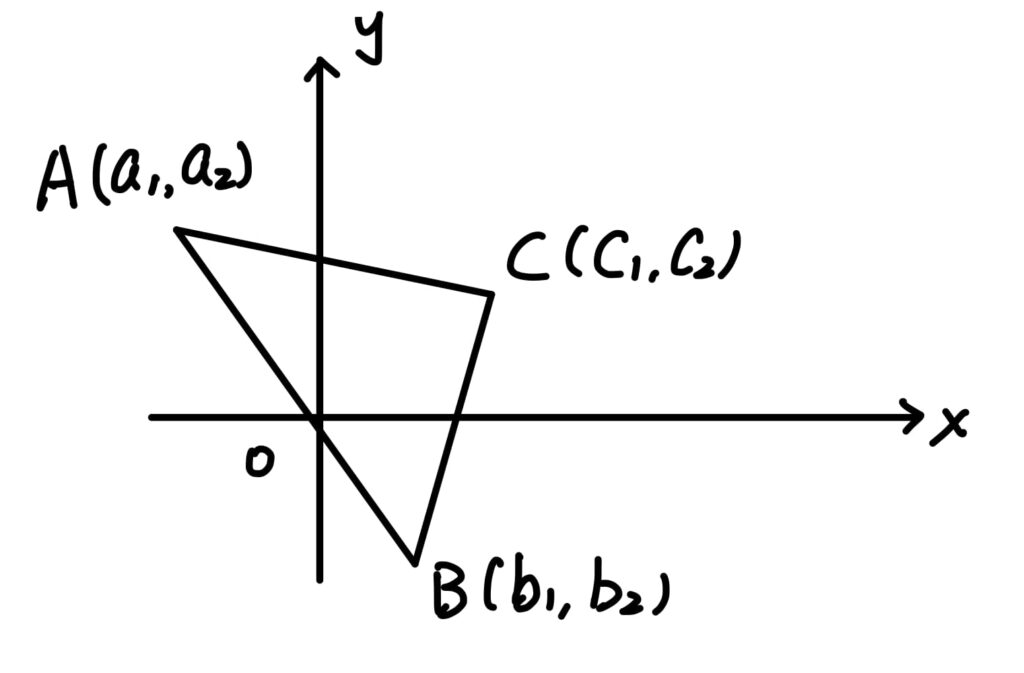
同樣地，往外補成一個矩形

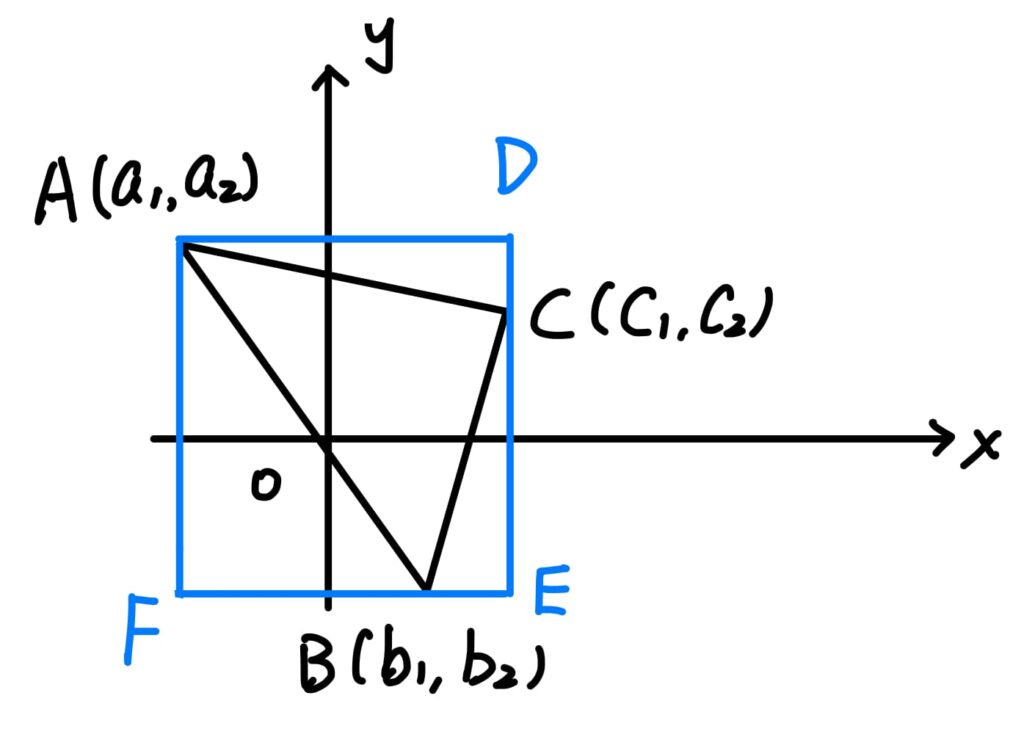
$$\begin{aligned}
\Delta ABC的面積 &=矩形AFED的面積 – \Delta ABF的面積 – \Delta BEC的面積 – \Delta ACD的面積 \\
&=(c_1-a_1)\cdot(a_2-b_2) – \frac{1}{2}\cdot (b_1-a_1)\cdot (a_2-b_2) \\
&- \frac{1}{2}(c_1-b_1)\cdot(c_2-b_2)-\frac{1}{2}\cdot(c_1-a_1)\cdot(a_2-c_2) \\
&= \frac{1}{2}\cdot(c_1a_2-a_1c_2) + \frac{1}{2}(b_1c_2-c_1b_2)+\frac{1}{2}(a_1b_2-a_2b_1) \\
\end{aligned}$$

接著從上式的規則，寫成「行列式」的符號如下：

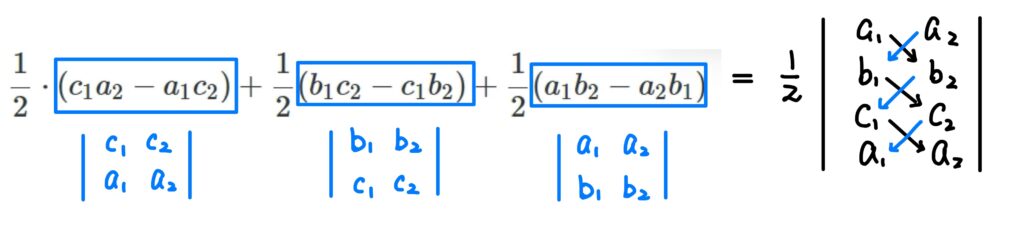
因為算出來的值為面積，如果不管頂點順序的話(依順時針或逆時針方向寫，結果會差個負號)，有可能會算出負數，最後再加個絕對值即可。

這篇文章就寫到這邊，提供給在學習中的讀者參考。

相關閱讀：【國中數學數位教學】如何學好國中數學？破除學習迷思，建立正確觀念？

2-2 二元一次方程式的圖形

第三章 比與比例式

3-1 比例式
3-2 正比與反比

第四章 一元一次不等式

4-1 認識一元一次不等式
4-2 解一元一次不等式

第五章 統計

5-1 統計圖表與資料分析

第六章 生活中的幾何

6-1 垂直、線對稱與三視圖