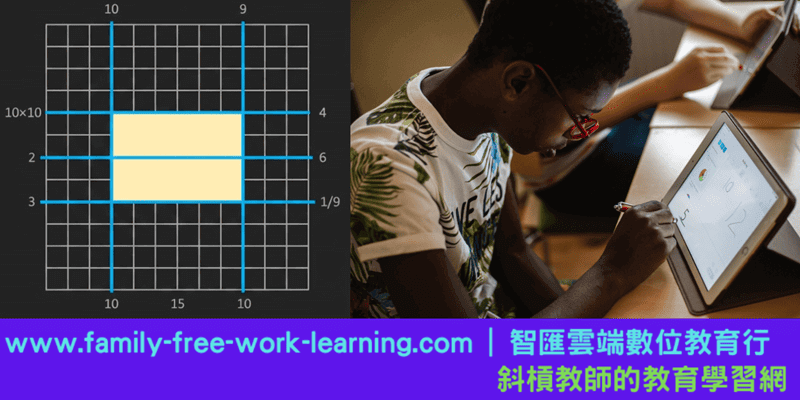
「如果你手邊有一張 \(n \times n\) 的格子紙，閉上眼睛，隨手選出四條線圍成一個矩形。
這個矩形可能很細長，也可能很寬扁。

但你有沒有想過，如果我們玩這個遊戲無窮多次，
這些隨機矩形的『平均面積』會是多少？

令隨機變數 \(X_n\) 表示所圍出的矩形面積，\(E(X_n)\) 表示 \(X_n\) 的期望值，
那麼

在 \(n \times n\) 的方格紙中隨機選取兩條縱線與兩條橫線，會圍成一個隨機矩形。
這是一個從離散組合跨越到連續機率的經典案例。

我們不急著跳入繁瑣的公式，先從結構開始觀察。

一、 結構拆解：從二維回歸一維

一個矩形的面積是由其寬度與高度相乘而得。

設矩形面積為隨機變數 \( X_n \)，寬度為 \( W \)，高度為 \( H \)。

由於橫線與縱線的選取是完全獨立且對稱的，我們可以利用期望值的性質，
將其簡化為： \[ E(X_n) = E(W \cdot H) = E(W) \cdot E(H) = [E(L)]^2 \]

這裡的 \( L \) 代表在範圍 \( [0, n] \) 的整數點中，
隨機選取兩個不重複點所形成的線段長度。

二、 邏輯推導：離散數列的求和

在 \( n+1 \) 條線中選取 2 條，總共有 \( C^{n+1}_{2} \) 種選法。

若選取的兩線段距離為 \( k \)（其中 \( 1 \le k \le n \)），
則這樣的組合共有 \( n-k+1 \) 種。

單一維度的期望長度 \( E(L) \) 計算如下：
\[ E(L) = \frac{\sum_{k=1}^{n} k \cdot (n-k+1)}{\frac{n(n+1)}{2}} \]

利用平方和與等差數列公式展開分子：
\[ \sum_{k=1}^{n} ( (n+1)k – k^2 ) = (n+1)\frac{n(n+1)}{2} – \frac{n(n+1)(2n+1)}{6} = \frac{n(n+1)(n+2)}{6} \]

因此，單一維度的平均長度為： \[ E(L) = \frac{\frac{n(n+1)(n+2)}{6}}{\frac{n(n+1)}{2}} = \frac{n+2}{3} \]

三、 極限分析：邁向連續空間

題目要求的是面積期望值與總面積 \( n^2 \) 之比在 \( n \) 趨近無限大時的極限。
當我們將結果帶入，會發現一個極其簡潔的常數：

\[ \lim_{n \to \infty} \frac{E(X_n)}{n^2} = \lim_{n \to \infty} \frac{(\frac{n+2}{3})^2}{n^2} = \lim_{n \to \infty} \frac{n^2 + 4n + 4}{9n^2} = \frac{1}{9} \]

四、 方法論比較

在處理這類機率問題時，不同的路徑能給我們不同的啟發：

\[ \begin{array}{|c|c|l|} \hline \text{方法路徑} & \text{主要工具} & \text{核心邏輯} \\ \hline \text{組合計數} & \text{級數求和} & \text{最紮實的離散基礎驗證} \\ \hline \text{微積分} & \int_0^1 \int_0^1 |x-y| dx dy & \text{將格子細分至無限，直接處理連續變數} \\ \hline \text{統計直觀} & \text{區間分點} & \text{隨機二點將線段均分為三段，平均長度為 1/3} \\ \hline \end{array} \]

這個 \( 1/9 \) 不僅僅是一個數字，它代表了在二維平面上，
隨機縮放的幾何體在長期平均下，會穩定在「邊長三分之一」的乘積結構中。

---