試著想像這樣一個場景:你站在美術館的一幅巨型畫作前。
這幅畫懸掛在高處,底端離地一段距離。
如果站得太遠,畫作顯得渺小;
如果貼得太近,視角又會變得極度傾斜,難以窺見全貌。
直覺告訴我們,在這兩者之間,一定存在一個「最佳觀賞點」,
能讓你的視角張開到最大。
這是一個自 15 世紀以來就困擾著測量學家的經典問題——
雷吉奥蒙塔努斯問題 (Regiomontanus’ problem)。
對於一般的學生,這是一道微積分的極值練習題;
但對於數學家來說,這是一場關於「圓」的幾何遊戲。
數學家的直覺:尋找那個「吻」
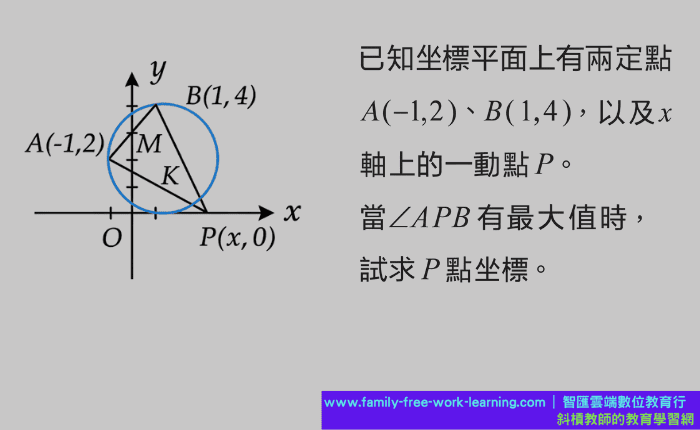
面對這個問題(已知 \(A\) , \(B\) 兩點,求 \(x\) 軸上一點 \(P\),使 \(\angle APB\) 最大),
一般的解題反射動作是設坐標、列三角函數、然後微分求極值。
但我們不妨先停下來畫圖。

已知一個幾何事實:「同弧所對的圓周角相等」。
這意味著,如果我們畫一個通過 \(A, B\) 兩點的圓,
那麼圓弧上任意一點對 \(A\), \(B\) 張開的角度都是一樣的。
想像有無數個通過 \(A\), \(B\) 的圓,圓愈大,圓弧愈平緩,張角就愈小;
圓愈小,圓弧愈彎曲,張角就愈大。
我們的目標,就是要把這個圓盡可能地「縮小」。
但是,\(P\) 點被限制在 \(x\) 軸上。
所以這個圓再怎麼縮小,都必須至少碰到 \(x\) 軸。
當圓大到割過 \(x\) 軸時,角度還不夠大;
當圓小到與 \(x\) 軸分離時,我們失去了 \(P\) 點;
唯有當這個圓與 \(x\) 軸「相切」的那一瞬間,圓最小,視角 \(\theta\) 最大。
此時\(P\)點的位置就呼之欲出。
代數的優雅驗證
有了幾何直觀,代數運算就不再是盲目的試誤,而是精準的導航。
讓我們用這道試題數據來驗證這個美麗的想法。
<方法1> 幾何作法
題目情境:
畫作的兩端分別在 \(A(-1, 2)\) 與 \(B(1, 4)\),觀測者站在 \(x\) 軸上的 \(P\) 點。
1. 幾何導航:
既然目標圓通過 \(A\), \(B\) 且切於 \(x\) 軸,那麼圓心 \(K\) 必須滿足兩個條件:
- 位於 \(A\), \(B\) 的中垂線上(幾何對稱性)。
- 圓心到 \(x\) 軸的距離等於半徑(相切條件)。
2. 鎖定圓心與切點:設圓心 \( K \) 坐標為 \( (h, 3-h) \)。
因為與 \( x \) 軸相切,半徑 \( R \) 即為圓心的 \( y \) 坐標高度 \( |3-h| \)。
同時,半徑也是 \( K \) 到 \( A \) 的距離。
我們列出等式: \[ \text{dist}(K, \text{x-axis})^2 = \text{dist}(K, A)^2 \]
代入座標距離公式: \[ (3-h)^2 = (h – (-1))^2 + ((3-h) – 2)^2 \] 展開這個式子,
你會驚訝地發現代數結構如幾何般對稱: \[ 9 – 6h + h^2 = (h^2 + 2h + 1) + (h^2 – 2h + 1) \]
整理後得到一個乾淨的二次方程式: \[ h^2 + 6h – 7 = 0 \] \[ (h+7)(h-1) = 0 \] 解得 \( h=1 \) 或 \( h=-7 \)。
因為切點 \( P \) 的 \( x \) 坐標即為圓心的 \( x \) 坐標 \( h \)(因為半徑垂直切線),
所以最佳觀測位置 \( P \) 就在 \( (1, 0) \) 或 \( (-7, 0) \)。
為了使角度愈大,因此圓要愈小,最後答案為 \((1, 0)\)。
<方法 2> 微積分:向量與極值分析
Step 1: 建立向量與目標函數
設 \( P(x, 0) \),我們利用向量內積與三角形面積公式來尋找 \(\tan \theta\) 的關係式。
向量設定: \[ \vec{PA} = (-1-x, 2), \quad \vec{PB} = (1-x, 4) \]
計算內積(Dot Product): \[ \vec{PA} \cdot \vec{PB} = (-1-x)(1-x) + (2)(4) = (x^2-1) + 8 = x^2 + 7 \]
利用面積公式(外積/行列式概念): \[ 2 \triangle APB = \left| \det(\vec{PA}, \vec{PB}) \right| = \left| \begin{matrix} -1-x & 1-x \\ 2 & 4 \end{matrix} \right| \] \[ = | 4(-1-x) – 2(1-x) | = | -4 – 4x – 2 + 2x | = | -2x – 6 | = 2|x+3| \]
利用正切公式 \(\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{2 \triangle APB}{\vec{{PA}} \cdot\vec{{PB}}}\),
可得目標函數:\[ \tan \theta(x) = \frac{2|x+3|}{x^2+7} \]
Step 2: 微分求極值
為了計算方便,我們針對 \(x > -3\) 的情形(使 \(x+3 > 0\))。
令函數 \(g(x)\) 為: \[ g(x) = \frac{x+3}{x^2+7} \]
使用除法微分公式(Quotient Rule): \[ g'(x) = \frac{(1)(x^2+7) – (x+3)(2x)}{(x^2+7)^2} \] \[ g'(x) = \frac{x^2 + 7 – 2x^2 – 6x}{(x^2+7)^2} = \frac{-x^2 – 6x + 7}{(x^2+7)^2} \]
Step 3: 解臨界點 (Critical Points)
令 \( g'(x) = 0 \) 以尋找極值發生點: \[ -x^2 – 6x + 7 = 0 \Rightarrow x^2 + 6x – 7 = 0 \] 因式分解: \[ (x+7)(x-1) = 0 \] 解得 \( x = -7 \) 或 \( x = 1 \)。
Step 4: 檢驗與結論
將 \(x\) 代回 \(g(x)\) 比較函數值: 當 \( x = -7 \) 時,\( g(-7) = \frac{-4}{56} < 0 \) (不合,因題目求最大視角),
當 \( x = 1 \) 時,\( g(1) = \frac{4}{8} = \frac{1}{2} \)。
畫個表格來看更清楚:

故當 \( x = 1 \) 時,\(\tan \theta(x)\) 達到最大值: \[ \tan \theta_{\max} = 2 \cdot g(1) = 2 \cdot \frac{1}{2} = 1 \]
此時 \( \theta = 45^\circ \),所求點為 \( P(1, 0) \)。
<方法 3> 代數視角:利用判別式求極值
如果你不想處理繁瑣的微分運算,代數提供了一條更快的捷徑。
我們將目標函數視為一個方程式,
利用 \( x \) 必須是實數(Real Number)的條件來反推最大值。
Step 1: 建立目標函數
利用直線夾角公式 \(\tan \theta = \left| \frac{m_1 – m_2}{1 + m_1 m_2} \right|\)。
設 \( P(x, 0) \),則兩直線斜率分別為:
\[ m_{PA} = \frac{0-2}{x-(-1)} = \frac{-2}{x+1}, \quad m_{PB} = \frac{0-4}{x-1} = \frac{-4}{x-1} \]

代入公式:
\[ \tan \theta(x) = \left| \frac{\frac{-2}{x+1} – \frac{-4}{x-1}}{1 + \left(\frac{-2}{x+1}\right)\left(\frac{-4}{x-1}\right)} \right| \]
上下同乘\((x+1)(x-1)\) 進行化簡:
\[ \text{分子} = -2(x-1) – (-4)(x+1) = -2x + 2 + 4x + 4 = 2x + 6 \]
\[ \text{分母} = (x+1)(x-1) + (-2)(-4) = (x^2 – 1) + 8 = x^2 + 7 \]
得到目標函數(令其為 \( K \)):
\[ \frac{2x+6}{x^2+7} = K \]
(註:此處討論 \( x \) 使分子分母同號或是取絕對值後的最大值情況,依計算過程 \( K \) 取正值)
Step 2: 轉化為二次方程式
將分母乘過去,整理成關於 \( x \) 的二次方程式:
\[ 2x + 6 = K(x^2 + 7) \]
\[ Kx^2 – 2x + (7K – 6) = 0 \]
Step 3: 利用判別式 \( D \ge 0 \)
因為 \( P \) 點坐標 \( x \) 必須是實數,故此二次方程式的判別式必須大於或等於 \(0\):
\[ D = b^2 – 4ac \ge 0 \]
\[ (-2)^2 – 4(K)(7K-6) \ge 0 \]
同除以 \(4\) 化簡:
\[ 1 – K(7K-6) \ge 0 \]
\[ 1 – 7K^2 + 6K \ge 0 \]
\[ 7K^2 – 6K – 1 \le 0 \]
因式分解:\[ (7K+1)(K-1) \le 0 \]
解不等式得 \( K \) 的範圍:\[ -\frac{1}{7} \le K \le 1 \]
Step 4: 結論
由上式可知,\(\tan \theta\) 的最大值(即 \( K \) 的最大值)為 \( 1 \)。
將 \( K=1 \) 代回原二次方程式求對應的 \( x \):
\[ 1 \cdot x^2 – 2x + (7\times 1 – 6) = 0 \]
\[ x^2 – 2x + 1 = 0 \]
\[ (x-1)^2 = 0 \Longrightarrow x = 1 \]
故當 \( x=1 \) 時,視角有最大值。
<方法 4> 算幾不等式:代數的極致簡化
這是所有解法中,計算量最少、最令人拍案叫絕的一招。
當你發現分子的變數可以透過「平移」消掉時,算幾不等式 (AM-GM Inequality) 就該登場了。
Step 1: 觀察結構與換元
目標函數為:
\[ \tan \theta(x) = \frac{2x+6}{x^2+7} = \frac{2(x+3)}{x^2+7} \]
觀察到分子是 \( 2(x+3) \),我們令 \( t = x+3 \)。
根據題目幾何情境(或是為了使正切值為正),我們考慮 \( t > 0 \) 的情況。
此時 \( x = t – 3 \)。
Step 2: 代入並化簡
將 \( x \) 替換為 \( t \):
\[ \text{式子} = \frac{2t}{(t-3)^2 + 7} = \frac{2t}{t^2 – 6t + 9 + 7} = \frac{2t}{t^2 – 6t + 16} \]
分子分母同除以 \( t \)(關鍵技巧:將變數集中到分母處理):
\[ \tan \theta(x) = \frac{2}{t – 6 + \frac{16}{t}} \]
Step 3: 使用算幾不等式
要讓整個分數最大,分母必須最小。
我們鎖定分母中的互倒數項 \( t + \frac{16}{t} \),利用算幾不等式 \( \frac{a+b}{2} \ge \sqrt{ab} \):
\[ \frac{t + \frac{16}{t}}{2} \ge \sqrt{t \cdot \frac{16}{t}} = \sqrt{16} = 4 \]
整理得:
\[ t + \frac{16}{t} \ge 8 \]
Step 4: 求極值與發生條件
將分母的最小值代回原式:
分母的最小值:\[ 8 – 6 = 2 \]
\[ \tan \theta_{\max} = \frac{2}{2} = 1 \]
等號成立條件(即極值發生瞬間):
\[ t = \frac{16}{t} \Rightarrow t^2 = 16 \]
因為 \( t > 0 \),取 \( t = 4 \)。
還原回 \( x \):
\[ x = t – 3 = 4 – 3 = 1 \]
故當 \( x = 1 \) 時,有最大視角。
在結束這趟數學探險之前,讓我們回頭看看這道有趣的題目。
若是為了考試,<方法 3> 判別式或 <方法 4> 算幾不等式 無疑是最佳策略,
它們像是一把鋒利的快刀,能迅速切開問題,取出答案 \( x=1\)。
但若是為了理解數學之美,則 <方法 1> 的幾何視角 更為巧妙。
微積分告訴我們「極值發生在導數為零處」,這是一個強大的計算結果;
但幾何學告訴我們「極值發生在圓與直線相切時」,這是一個美麗的結構洞察。
當雷吉奥蒙塔努斯在 15 世紀提出這個問題時,微積分尚未誕生。
他仰賴的正是對圖形敏銳的直覺。
今天的我們,雖然擁有了微積分這項重型武器,但「看見結構」的能力依然無可取代。
下次當你面對一道棘手的極值問題時,不妨先停下急著計算的筆,試著在腦海中畫個圖。
也許你會發現,答案不在繁雜的公式裡,而在那個輕輕觸碰的切點上。
【想看更多?】 如果你喜歡這種「一題多解」的數學分析,歡迎訂閱我的電子報,
之後我們都會從一道經典試題出發,挖掘背後深刻的數學故事。